当前位置:网站首页>单变量线性回归
单变量线性回归
2022-08-05 05:15:00 【春天猪会飞】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
前言
一开始学习AI会有些迷茫,因为体系非常庞大,没关系,道虽远不行不至。直接开干。
一、模型描述
单变量线性回归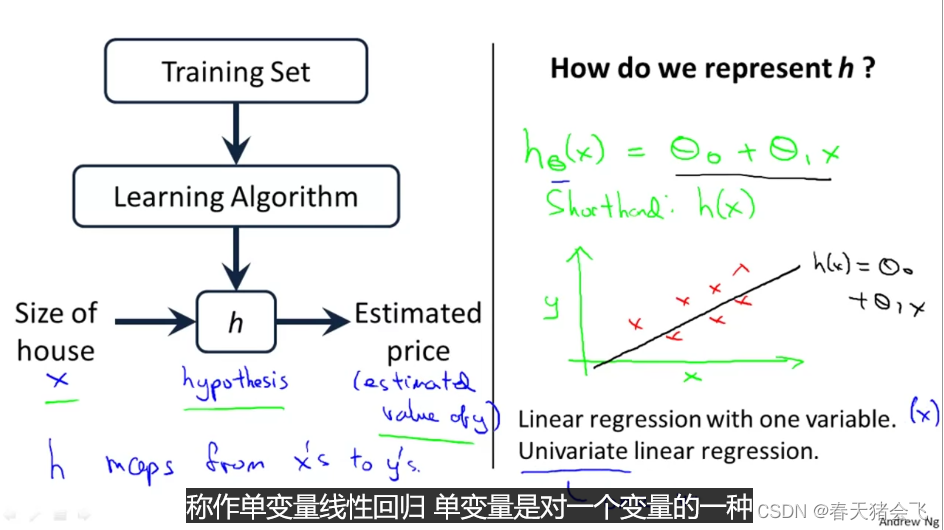 目标就是得到h(x),hypothesis这个叫法是一个历史遗留问题,虽然不是很恰当,但亦可理解。
目标就是得到h(x),hypothesis这个叫法是一个历史遗留问题,虽然不是很恰当,但亦可理解。
二、代价函数
吴恩达课件内容: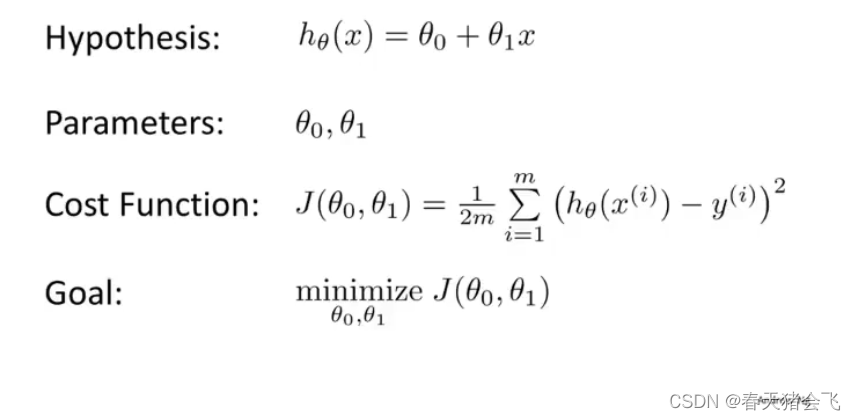
代价函数也被称为平方误差函数,有时也被称为平方误差代价函数
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))
其中 x i x^{i} xi和 y i y^{i} yi表示第i组训练样本,m为训练样本数量
平方误差代价函数是解决回归问题最常用的手段
代价函数(一)
首先是默认将常数项设为0,这时可以看到当 θ 1 \theta_{1} θ1为1的时候代价函数取到最小值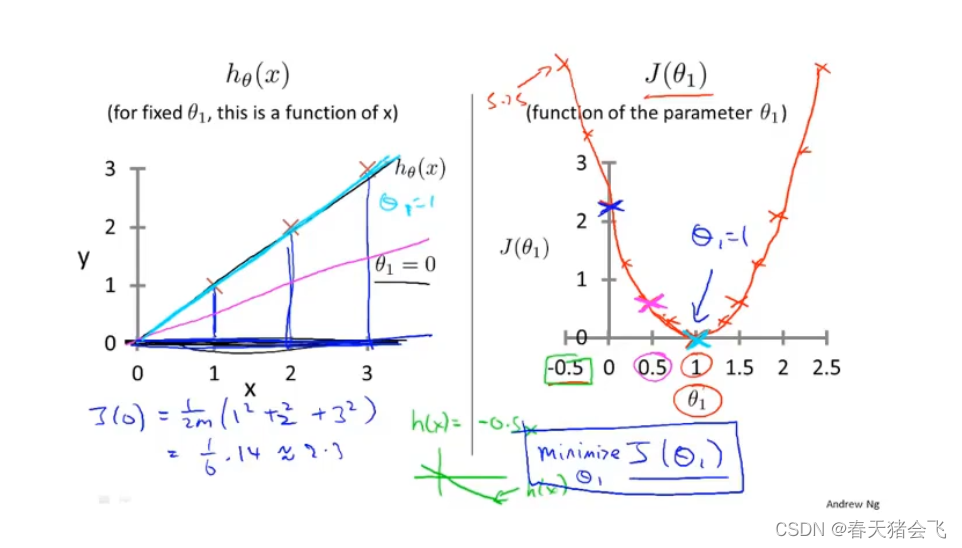
代价函数(二)
θ 0 \theta_{0} θ0和 θ 1 \theta_{1} θ1都在变化的时候代价函数呈现出来的如下所示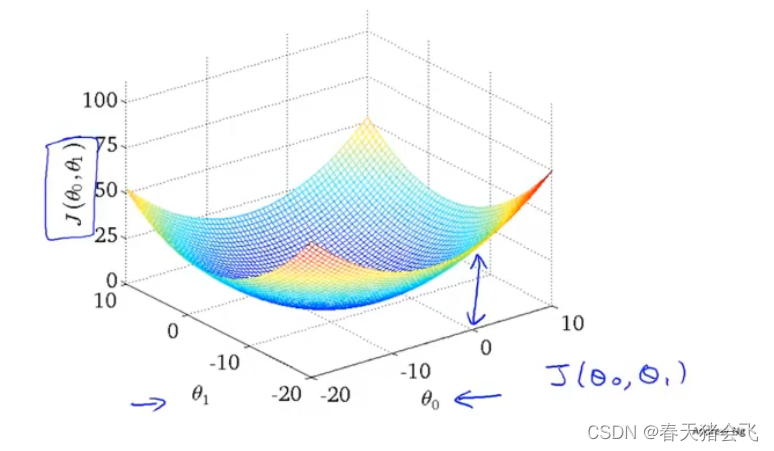
三、梯度下降
想象一下一种方法,通过不断的改变 θ i \theta_{i} θi来获得代价函数的最小值(可能是局部最优)。
这里引入吴恩达的方法,想象站在一个山坡上,环顾四周,找一个最快下山的路。
没错,就是最大方向导数,也就是梯度,吴恩达以两个参数为例的梯度下降算法:
θ j : = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) \theta_{j}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right) θj:=θj−α∂θj∂J(θ0,θ1)
α \alpha α被我们称为学习率(learning rate)
这里有一个注意事项, θ i \theta_{i} θi对应的每一个参数都需要同时更新,以确保这是梯度下降算法的实现,否则可能成为了别的什么场合下的算法。
四、梯度下降知识点总结
假如代价函数仅有一个参数,这时候如何理解梯度下降算法?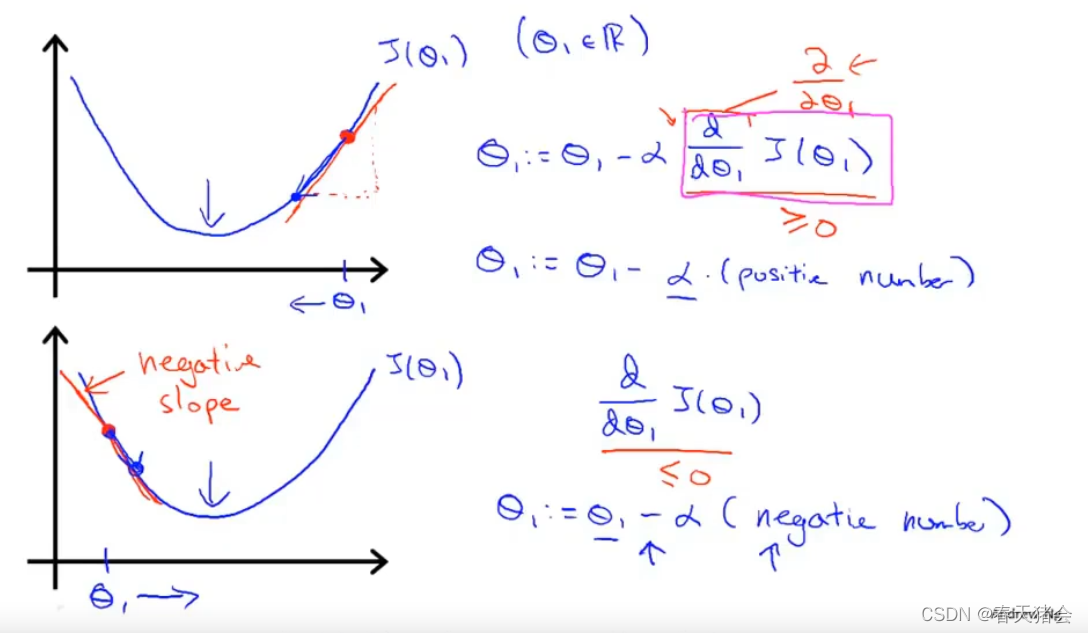 可以看到,确实通过这个算法,可以使得代价函数不断逼近最小值
可以看到,确实通过这个算法,可以使得代价函数不断逼近最小值
有关 α \alpha α
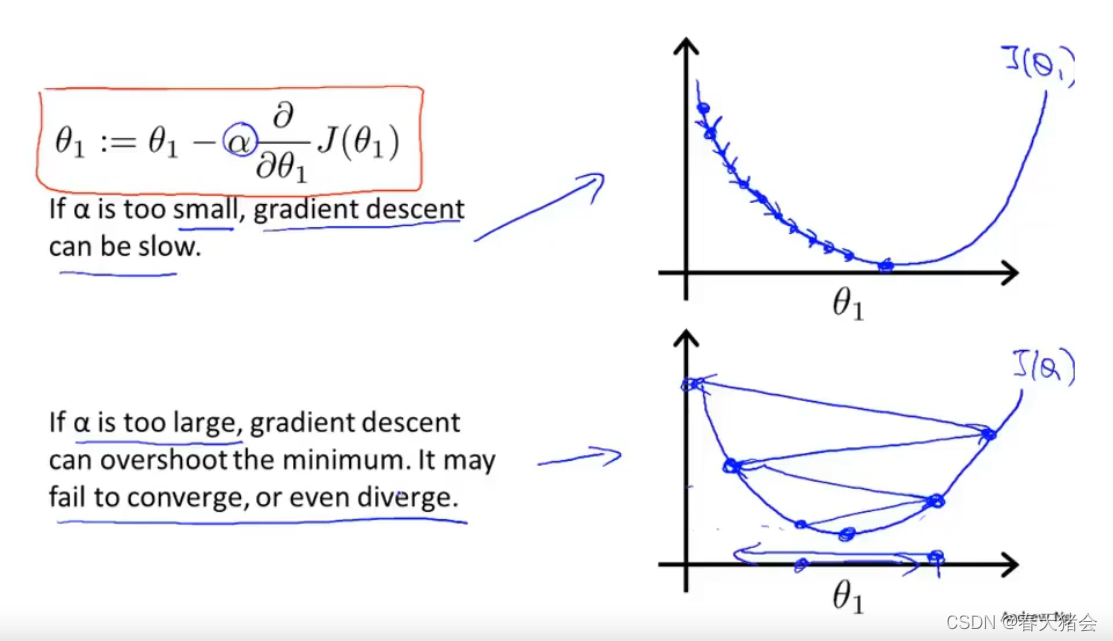
梯度下降算法更新到局部最优点,具备保持
如果初始化就在最优位置: 这也解释了,为什么即使不改变学习率 α \alpha α,最终代价函数也能收敛到局部最低点的原因。
这也解释了,为什么即使不改变学习率 α \alpha α,最终代价函数也能收敛到局部最低点的原因。
因为随着梯度下降,导数项会越来越小。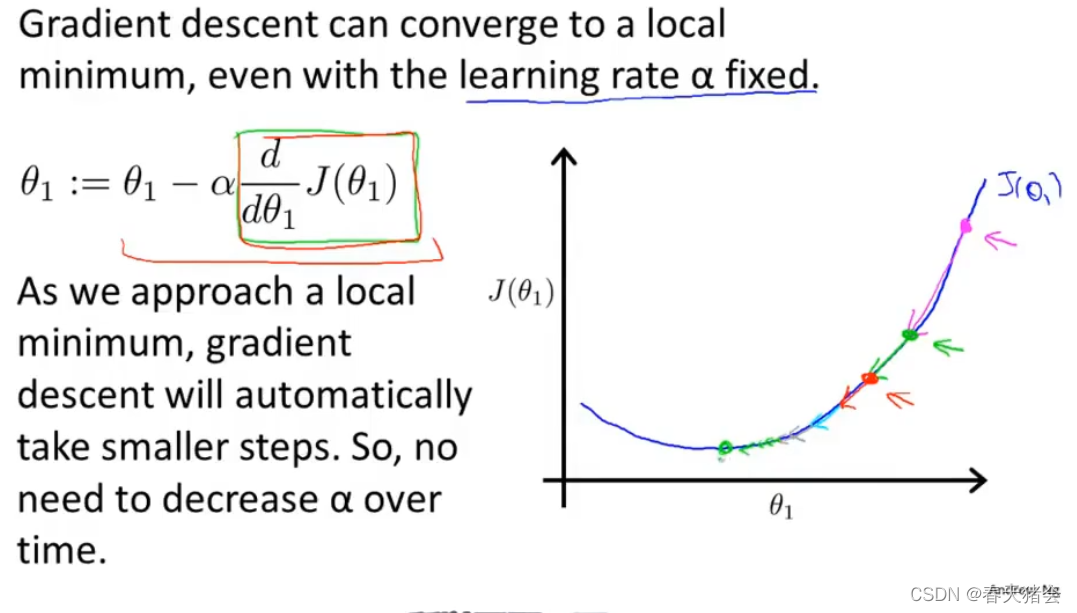
五、线性回归的梯度下降
总结
今天主要是学习的线性回归模型,以及对应这个模型的代价函数——平方误差代价函数,难度不是很高,很快上手吧。
边栏推荐
猜你喜欢
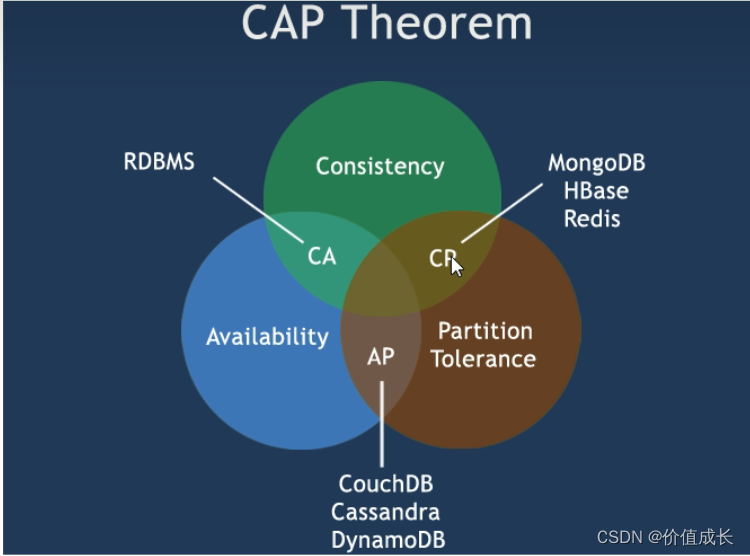
CAP+BASE
【数据库和SQL学习笔记】5.SELECT查询3:多表查询、连接查询
![[After a 12] No record for a whole week](/img/05/df9aeb04274e308e1341020f836821.jpg)
[After a 12] No record for a whole week
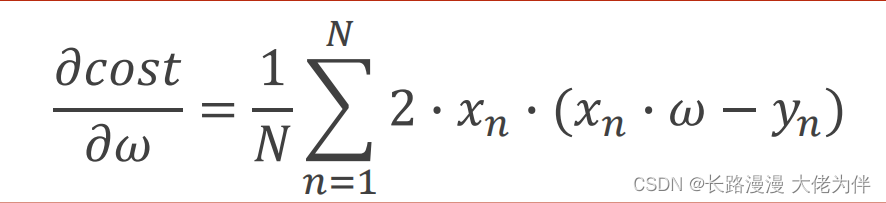
Lecture 3 Gradient Tutorial Gradient Descent and Stochastic Gradient Descent
spingboot 容器项目完成CICD部署
flink部署操作-flink standalone集群安装部署

flink yarn-session的两种使用方式
flink实例开发-详细使用指南
SQL(1) - Add, delete, modify and search
![[Let's pass 14] A day in the study room](/img/fc/ff4161db8ed13a0c8ef75b066b8eab.png)
[Let's pass 14] A day in the study room
随机推荐
BFC(Block Formatting Context)
day11-函数作业
flink基本原理及应用场景分析
面向小白的深度学习代码库,一行代码实现30+中attention机制。
全尺度表示的上下文非局部对齐
Kubernetes常备技能
Matplotlib(一)—— 基础
学习总结week2_4
用GAN的方法来进行图片匹配!休斯顿大学提出用于文本图像匹配的对抗表示学习,消除模态差异!
CVPR best paper winner Huang Gao's team from Tsinghua University presented the first dynamic network review
[Go through 10] sklearn usage record
大型Web网站高并发架构方案
学习总结week2_3
服务网格istio 1.12.x安装
【Kaggle项目实战记录】一个图片分类项目的步骤和思路分享——以树叶分类为例(用Pytorch)
ECCV2022 | RU&谷歌提出用CLIP进行zero-shot目标检测!
【Reading】Long-term update
基于Flink CDC实现实时数据采集(一)-接口设计
数据库期末考试,选择、判断、填空题汇总
spark-DataFrame数据插入mysql性能优化