当前位置:网站首页>Notes of training courses selected by Massey school
Notes of training courses selected by Massey school
2022-07-07 00:27:00 【Evergreen AAS】
Multivariate statistical analysis
Clustering analysis
characteristic :
- I don't know the number and structure of categories in advance ;
- The data to be analyzed is the similarity or dissimilarity between objects ( distance );
- Put objects close together .
classification
- According to different classification objects, it can be divided into
- Q Type clustering : Cluster the samples
- R Type clustering : Cluster variables
- According to the clustering method, it is mainly divided into
- Systematic clustering
- Dynamic clustering
distance
Minikowski distance :
d(x,y) = [\sum\limits_{k=1}^p|x_{k} - y_{k}|^{m}]^{\frac{1}{m}}, x,y by p Virial vector
- m = 1 when , Is absolute distance
- m = 2 when , For Euclidean distance
- m = \infty, For Chebyshev distance , namely \mathop{max}\limits_{1\le k \le p}|x_{k} - y_{k}|
Mahalanobis distance ( Commonly used in cluster analysis )
d(x,y) = \sqrt{(x - y)^{T} \sum\nolimits^{-1} (x - y)}
among x, y For coming from p Dimensional population Z Sample observations of ,Σ by Z The covariance matrix of , In the actual Σ Often do not know , It is often necessary to estimate with sample covariance . Markov distance is invariant to all linear transformations , Therefore, it is not affected by dimensions .
R sentence :
dist(x,method=“euclidean”, diag=FALSE, upper=FALSE, p=2)
- method: The way to calculate the distance
- “euclidean”: Euclidean distance
- “maximum”: Chebyshev distance
- “manhattan”: Absolute distance
- “minkowski”: Minkowski distance ,p yes Minkowski Order of distance
- diag=TRUE: Output the distance on the diagonal
- upper=TRUE: Output the value of the upper triangular matrix ( The default value is only output The value of trigonometric matrix )
python sentence :
import rpy2.robjects as robjects x = [1, 2, 6, 8, 11] r = robjects.r res = r.dist(x) print(res) # 1 2 3 4 # 2 1 # 3 5 4 # 4 7 6 2 # 5 10 9 5 3
import rpy2 import rpy2.robjects.numpy2ri R = rpy2.robjects.r r_code = """ x<-c(1,2,6,8,11) y<-dist(x) print(y) """ R(r_code)
- notes : I use rpy2 It's hard to realize this feeling . It may not be possible to learn from python call R Language , Direct use recommended R Language
Standardized treatment
When the measured values of indicators differ greatly , The data should be standardized first , Then use the standardized data to calculate the distance .
General standardized transformation
X_{ij}^{*} = \frac{X_{ij} - \overline{X}_{j}}{S_{j}}
i=1,2,…n It means the first one i Samples ,j=1,2,…p Represents the... Of the sample j Indicators , Each sample has p Two observation indicators . It's No j Sample mean of indicators
Range standardization transformation
X_{ij}^{*} = \frac{X_{ij} - \overline{X}_{j}}{R_{j}} \\ among ,R_{j} = \mathop{\max}\limits_{1\le k \le n}X_{kj} - \mathop{\max}\limits_{1 \le k \le n}X_{kj}
Range normalization transformation
X_{ij}^{*} = \frac{X_{ij} - \mathop{\min}\limits_{1\le k\le n} X_{kj}}{R_{j}}
Program statement
Centralization and standardization of data
R sentence
scale(X,center = True, scale = True)
X: Sample data matrix ,center = TURE Means to make centralized transformation of data ,scale=TRUE It means to make standardized changes to the data
python sentence
import rpy2 import numpy import rpy2.robjects.numpy2ri rpy2.robjects.numpy2ri.activate() R = rpy2.robjects.r x = numpy.array([[1.0, 2.0], [3.0, 1.0]]) res = R.scale(x, center=True, scale=True) print(res)
The data is subject to extreme standardization
x <- data.frame(
points = c(99, 97, 104, 79, 84, 88, 91, 99),
rebounds = c(34, 40, 41, 38, 29, 30, 22, 25),
blocks = c(12, 8, 8, 7, 8, 11, 6, 7)
)
# apply() Function must be applied to dataframe or matrix
center <- sweep(x, 2, apply(x, 2, mean))
R <- apply(x, 2, max) - apply(x, 2, min)
x_star <- sweep(center, 2, R, "/")
# if x_star<-sweep(center, 2, sd(x), "/"), Then we get ( Ordinary ) Standardized transformed data ;
print(x_star)sweep(x, MARGIN, STATS, FUN=”-“, …)
- x: Array or matrix ;MARGIN: Operation area , The matrix 1 Said line ,2 The column ;
- STATS It's statistics ,apply(x, 2, mean) Represents the mean value of each column ;
- FUN Represents the operation of a function , The default value is subtraction .
Similarity coefficient
Calculate the correlation coefficient between different indicators of the sample , It is suitable for clustering variables .
Systematic clustering
Cluster analysis is the most commonly used
The basic idea
- (1) Depending on each sample ( Or variable ) Self becoming , Specify the distance between classes ( Or the coefficient of similarity );
- (2) Take the most similar sample ( Or variable ) Gather into small categories , Then aggregate the aggregated subclasses according to similarity ;
- (3) Finally, all subclasses are aggregated into a large class , Thus, we can get a pedigree relationship gathered according to the size of similarity
3. According to different definitions of distance, it can be divided into
- (1) The shortest distance method : The distance between classes is defined as the distance between the nearest samples in the two classes ;
- (2) The longest distance method : The distance between classes is defined as the distance between the farthest samples in the two classes ;
- (3) Class average method : The distance between classes is defined as the average of the distance between two samples in two classes ;
Program
x<-c(1,2,6,8,11); dim(x)<-c(5,1); d<-dist(x) # Generate distance structure hc1<-hclust(d, "single"); hc2<-hclust(d, "complete") hc3<-hclust(d, "median"); hc4<-hclust(d, "mcquitty") # Generate systematic clustering opar <- par(mfrow = c(2, 2)) plot(hc1,hang=-1); plot(hc2,hang=-1) plot(hc3,hang=-1); plot(hc4,hang=-1) par(opar)# Draw all tree structure diagrams , With 2*2 The form of is drawn on a picture
hclust(): Calculate the systematic clustering plot(): Draw a tree diagram of systematic clustering hclust(d, method = “complete”) d:dist Distance structure , method: The method of systematic clustering ( The default is the longest distance method ), The parameters are : (1)“single”: The shortest distance method (2)“complete”: The longest distance method (3)“average”: Class average method …… plot(x, labels = NULL, hang = 0.1, main = “Cluster Dendrogram”, sb = NULL, xlab = NULL, ylab =”Height”, …)
x: hclust() The object generated by the function hang: Indicate the positions of various types in the tree , Taking a negative value means that the classes in the tree are drawn from the bottom main: Drawing name
Dynamic clustering
System clustering : Once the class is formed, it will not change ; Dynamic clustering : Stepwise clustering
The basic idea
First, roughly classify , Then modify the unreasonable classification according to some optimal principle , Until the score is reasonable , Form the final classification result .
Program
kmeans(x, centers, iter.max=10, nstart=1, algorithm*=c(“Hartigan-Wong”, “Lloyd”, “MacQueen”))
- x It is a matrix or data frame composed of data ,
- centers Is the number of clusters or the center of the initial class ,
- iter.max Is the maximum number of iterations ( The maximum value is 10),
- nstart Is the number of random sets ,
- algorithm It is a dynamic clustering algorithm .
X<-data.frame(
x1=c(2959.19, 2459.77, 1495.63, 1046.33, 1303.97, 1730.84, 1561.86, 1410.11, 3712.31, 2207.58, 2629.16, 1844.78, 2709.46, 1563.78, 1675.75, 1427.65, 1783.43, 1942.23, 3055.17, 2033.87, 2057.86, 2303.29, 1974.28, 1673.82, 2194.25, 2646.61, 1472.95, 1525.57, 1654.69, 1375.46, 1608.82),
x2=c(730.79, 495.47, 515.90, 477.77, 524.29, 553.90, 492.42, 510.71, 550.74, 449.37, 557.32, 430.29, 428.11, 303.65, 613.32, 431.79, 511.88, 512.27, 353.23, 300.82, 186.44, 589.99, 507.76, 437.75, 537.01, 839.70, 390.89, 472.98, 437.77, 480.99, 536.05),
x3=c(749.41, 697.33, 362.37, 290.15, 254.83, 246.91, 200.49, 211.88, 893.37, 572.40, 689.73, 271.28, 334.12, 233.81, 550.71, 288.55, 282.84, 401.39, 564.56, 338.65, 202.72, 516.21, 344.79, 461.61, 369.07, 204.44, 447.95, 328.90, 258.78, 273.84, 432.46),
x4=c(513.34, 302.87, 285.32, 208.57, 192.17, 279.81, 218.36, 277.11, 346.93, 211.92, 435.69, 126.33, 160.77, 107.90, 219.79, 208.14, 201.01, 206.06, 356.27, 157.78, 171.79, 236.55, 203.21, 153.32, 249.54, 209.11, 259.51, 219.86, 303.00, 317.32, 235.82),
x5=c(467.87, 284.19, 272.95, 201.50, 249.81, 239.18, 220.69, 224.65, 527.00, 302.09, 514.66, 250.56, 405.14, 209.70,272.59, 217.00, 237.60, 321.29, 811.88, 329.06, 329.65, 403.92, 240.24, 254.66, 290.84, 379.30, 230.61, 206.65, 244.93, 251.08, 250.28),
x6=c(1141.82, 735.97, 540.58, 414.72, 463.09, 445.20, 459.62, 376.82, 1034.98, 585.23, 795.87, 513.18, 461.67, 393.99, 599.43, 337.76, 617.74, 697.22, 873.06, 621.74, 477.17, 730.05, 575.10, 445.59, 561.91, 371.04, 490.90, 449.69, 479.53, 424.75, 541.30),
x7=c(478.42, 570.84, 364.91, 281.84, 287.87, 330.24, 360.48, 317.61, 720.33, 429.77, 575.76, 314.00, 535.13, 509.39, 371.62, 421.31, 523.52, 492.60, 1082.82, 587.02, 312.93,438.41, 430.36, 346.11, 407.70, 269.59, 469.10, 249.66, 288.56, 228.73, 344.85),
x8=c(457.64, 305.08, 188.63, 212.10, 192.96, 163.86, 147.76, 152.85, 462.03, 252.54, 323.36, 151.39, 232.29, 160.12, 211.84, 165.32, 182.52, 226.45, 420.81, 218.27, 279.19, 225.80, 223.46, 191.48, 330.95, 389.33, 191.34, 228.19, 236.51, 195.93, 214.40),
row.names = c(" Beijing ", " tianjin ", " hebei ", " shanxi ", " Inner Mongolia ", " liaoning ", " Ji Lin ", " heilongjiang ", " Shanghai ", " jiangsu ", " Zhejiang ", " anhui ", " fujian ", " jiangxi ", " Shandong ", " Henan ", " hubei ", " hunan ", " guangdong ", " guangxi ", " hainan ", " Chongqing ", " sichuan ", " guizhou ", " yunnan ", " Tibet ", " shaanxi ", " gansu ", " qinghai ", " ningxia ", " xinjiang ")
)
kmeans(scale(X),5)
K-means clustering with 5 clusters of sizes 10, 7, 3, 7, 4
Clustering vector:
Beijing tianjin hebei shanxi Inner Mongolia liaoning Ji Lin heilongjiang Shanghai jiangsu
5 4 3 3 3 3 3 3 5 4
Zhejiang anhui fujian jiangxi Shandong Henan hubei hunan guangdong guangxi
5 1 2 1 4 1 1 4 5 2
hainan Chongqing sichuan guizhou yunnan Tibet shaanxi gansu qinghai ningxia
2 4 1 1 4 4 1 3 3 3
xinjiang
3Principal component analysis
The basic idea
The importance of variables in practical problems is different , And there is a certain correlation between many variables . These variables are transformed through this correlation , Use a small number of new variables to reflect most of the information provided by the original variables , Simplify the original problem . That is, data dimensionality reduction
Principal component analysis is a statistical method for processing high-dimensional data under this dimensionality reduction idea .
The basic method
By properly constructing the linear combination of original variables , Generate a new list of unrelated variables , Select a few new variables and make them contain as much information as the original variables , Thus, a few new variables are used to replace the original variables , To analyze the original problem .
The variable contains “ Information ” The size of is usually measured by the variance of the variable or the sample variance .
Such as constant a,Var(a) = 0 , We go through a, I can only know a This constant , It contains little information .
Definition of principal component
set up X = (X_{1}, X_{2},……,X_{p})^{T} For practical problems involved p A vector of random variables , remember X The mean of \mu, The covariance matrix is \sum.
Consider linear combinations
\left\{ \begin{aligned} Y_{1} & = & a_{1}^{T}X \\ . \\ . \\ Y_{p} & = & a_{p}^{T}X \\ \end{aligned} \right.
………………………………………………………………………………………………………
warning: Just write the code
Program
Find the eigenvalue and eigenvector of the matrix
a <- c(1, -2, 0, -2, 5, 0, 0, 0, 2) # By vector a Construction one 3 Columns of the matrix , byrow=T The data representing the generated matrix is placed in rows ; b <- matrix(data = a, ncol = 3, byrow = T) c <- eigen(b) # seek b Eigenvalues and eigenvectors of
Linear model
1. The relationship between variables is generally divided into two categories
- Completely certain relationship , It can be expressed as a function analytic expression
- Uncertain relationship , Also known as correlation
2. The main content of regression analysis
- Through observation or processing of experimental data , Find out the quantitative mathematical expression of the correlation coefficient between variables — Empirical formula , That is, parameter estimation , And determine the specific form of empirical regression equation
- Test whether the established empirical regression equation is reasonable
- Use a reasonable regression equation for random variables Y Predict and control .
边栏推荐
- 如何判断一个数组中的元素包含一个对象的所有属性值
- Business process testing based on functional testing
- Oracle EMCC 13.5 environment in docker every minute
- Use package FY in Oracle_ Recover_ Data. PCK to recover the table of truncate misoperation
- Use Yum or up2date to install the postgresql13.3 database
- Understand the misunderstanding of programmers: Chinese programmers in the eyes of Western programmers
- web渗透测试是什么_渗透实战
- [CVPR 2022] semi supervised object detection: dense learning based semi supervised object detection
- Data analysis course notes (III) array shape and calculation, numpy storage / reading data, indexing, slicing and splicing
- 基于SSM框架的文章管理系统
猜你喜欢
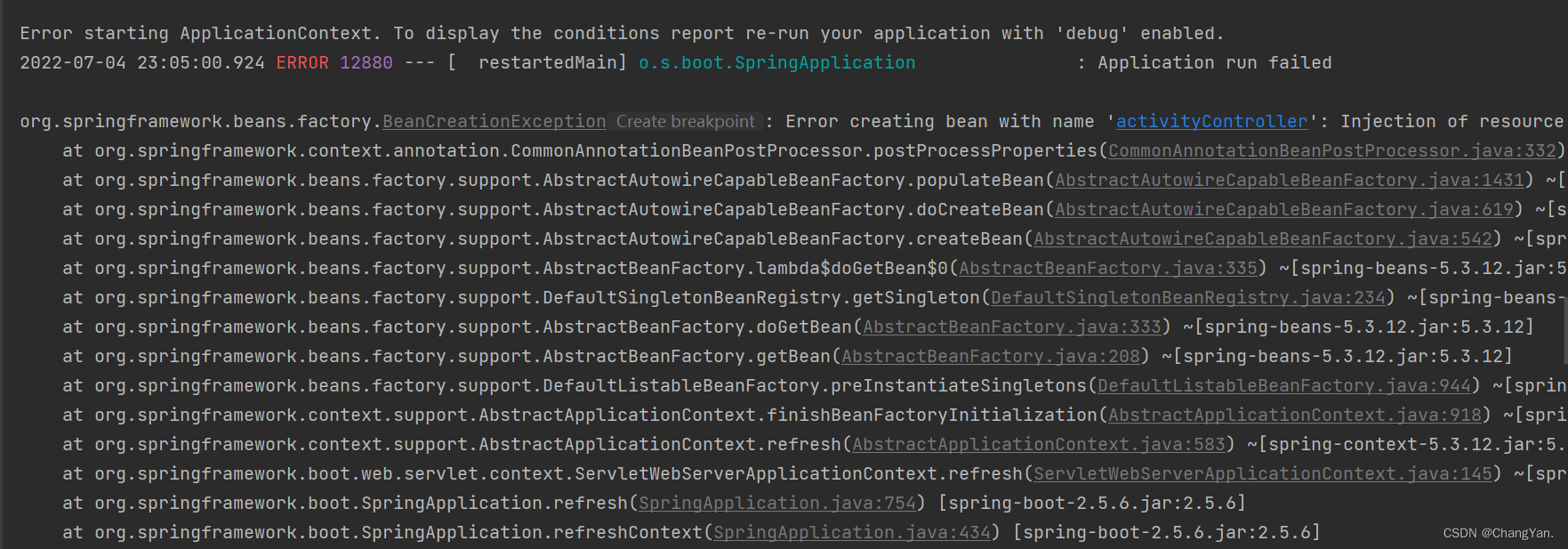
@TableId can‘t more than one in Class: “com.example.CloseContactSearcher.entity.Activity“.

准备好在CI/CD中自动化持续部署了吗?

DAY FOUR
VTK volume rendering program design of 3D scanned volume data

37頁數字鄉村振興智慧農業整體規劃建設方案

专为决策树打造,新加坡国立大学&清华大学联合提出快速安全的联邦学习新系统
Imeta | Chen Chengjie / Xia Rui of South China Agricultural University released a simple method of constructing Circos map by tbtools
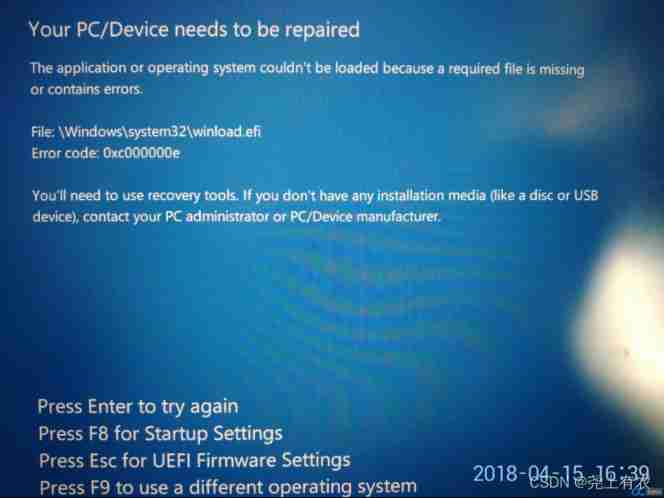
Win10 startup error, press F9 to enter how to repair?
GPIO簡介
uniapp实现从本地上传头像并显示,同时将头像转化为base64格式存储在mysql数据库中
随机推荐
Oracle EMCC 13.5 environment in docker every minute
PostgreSQL高可用之repmgr(1主2从+1witness)+Pgpool-II实现主从切换+读写分离
智能运维应用之道,告别企业数字化转型危机
【2022全网最细】接口测试一般怎么测?接口测试的流程和步骤
C language input / output stream and file operation [II]
Command line kills window process
2022年PMP项目管理考试敏捷知识点(9)
什么是响应式对象?响应式对象的创建过程?
Amazon MemoryDB for Redis 和 Amazon ElastiCache for Redis 的内存优化
PostgreSQL使用Pgpool-II实现读写分离+负载均衡
[2022 the finest in the whole network] how to test the interface test generally? Process and steps of interface test
Compilation of kickstart file
ldap创建公司组织、人员
DAY FIVE
在docker中快速使用各个版本的PostgreSQL数据库
MySQL主从之多源复制(3主1从)搭建及同步测试
Introduction au GPIO
DAY ONE
DAY TWO
@TableId can‘t more than one in Class: “com.example.CloseContactSearcher.entity.Activity“.