Abstract : In the game , Just a little mouse click , The system immediately looks for the closest route to the character . What is the mystery of the behavioral logic behind this ?
author :JohnserfSeed
In the game , When we need to move a character to a specific location , This simple step can be accomplished with a little mouse click , The system immediately looks for the closest route to the character .
But , What is the mystery of the behavioral logic behind this ? How would you write this pathfinding algorithm ?
Generally, we encounter this kind of path search problem , The first thing you can think of is breadth first search algorithm (Breadth First Search)、 And depth first (Depth First Search)、 Freud (Floyd)、 dijkstra (Dij) And so on, these very famous path search algorithms , But in most cases, the shortcomings of these algorithms are exposed : Time complexity is high .
therefore , In most environments, we use a name called A* (A star) Search algorithm
When it comes to the shortest path , We have to mention breadth first traversal (BFS), It's a universal algorithm , It's not just for On the question of finding a way or searching .windows System Tools : Drawing board The paint barrel in is a typical example .

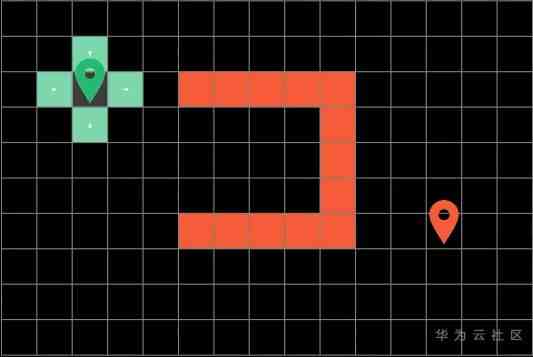
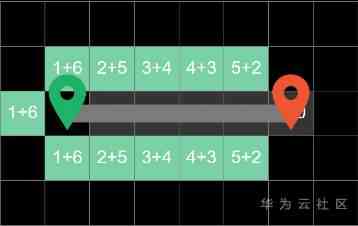
Here is a simple example of path search

Suppose we search for the shortest path on a grid
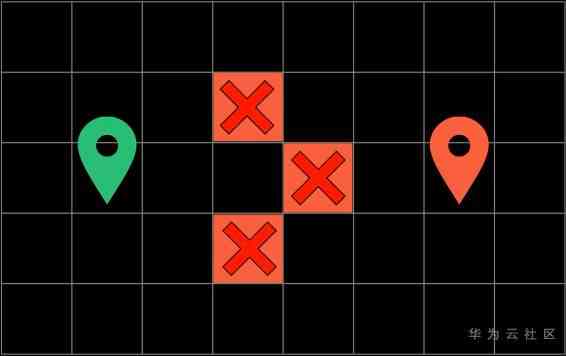
We can only move up and down , Do not cross obstacles . The purpose of the algorithm is to let you find a shortest path from the starting point to the site
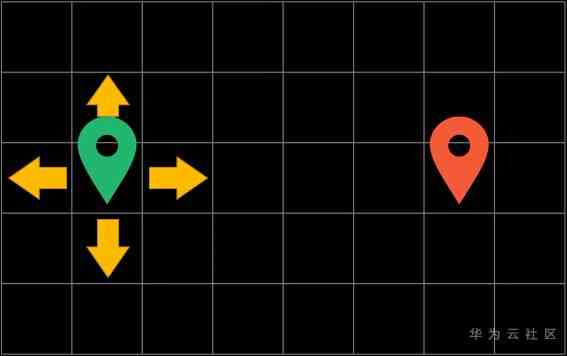
Suppose you can go up and down, left and right every time 4 Move in one direction
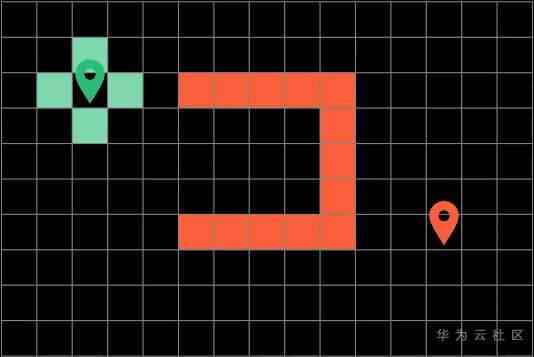
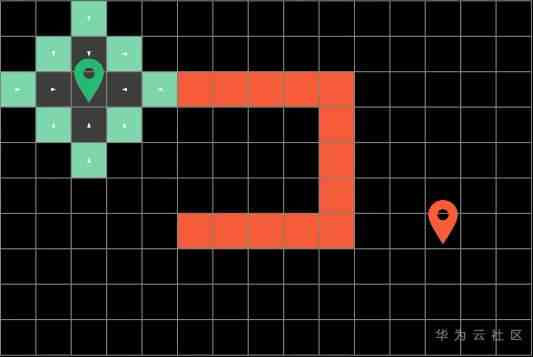
After each round of traversal, the algorithm marks the blocks explored in this round, which is called boundary (Frontier), These are the green squares .
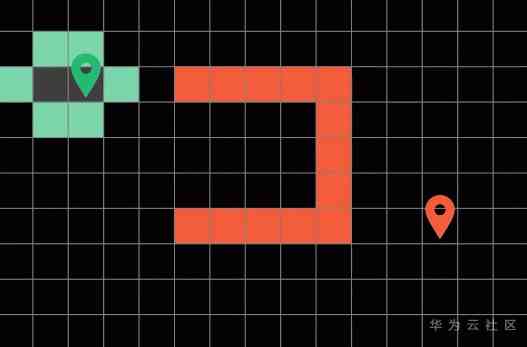
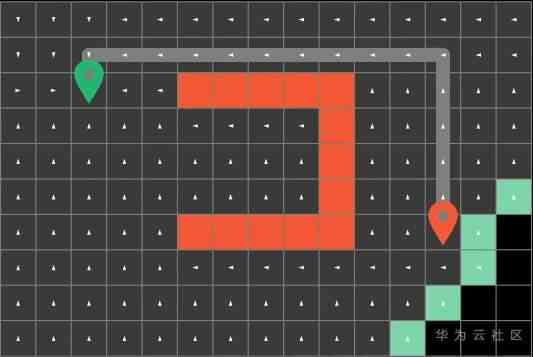
Then the algorithm will start from these boundary blocks in a circular way , Explore them up and down, left and right , Until the algorithm traverses to the end of the square will not stop . The shortest path is the path explored by the algorithm before . In order to get the whole path explored by the algorithm , We can record the direction of the path in the process of searching .
For example, the white arrow on the square represents the position of the previous block
Every time we explore the path , All we have to do is record this extra information
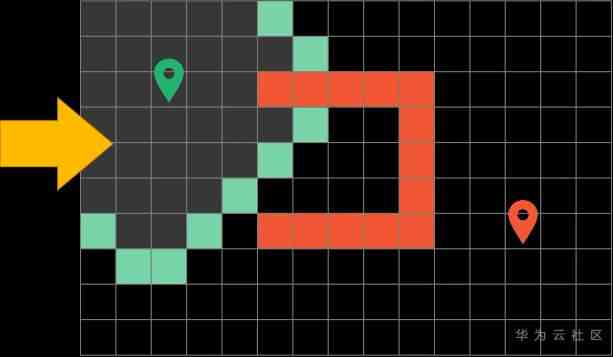
it is to be noted that , All the paths we've explored need to be marked gray , On behalf of them “ Has been visited “, In this way, the sub algorithm will not repeatedly explore the path that has been taken .
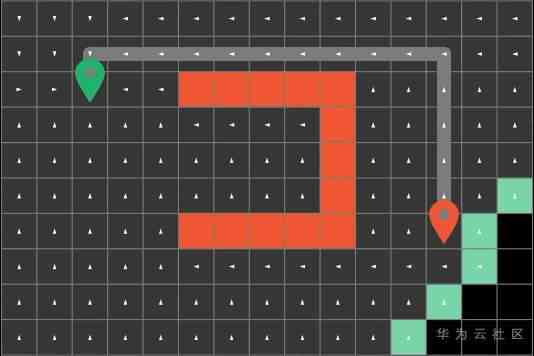
Breadth first algorithm can obviously help us find the shortest path , But it's a little silly , Because its search for the path is not directional , It will probe in all directions .

The worst case scenario is to traverse the entire map , So it's not smart , We need a more efficient algorithm .
That's what we're going to introduce this time A * (A star) search algorithm
A* Search Algorithm
”A* search algorithm “ It's also called “ Heuristic search ”
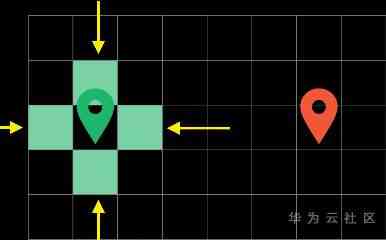
What's different from breadth first is , We don't explore all the boundary blocks in each cycle (Frontier), And will choose the current “ cost (cost)” The lowest box to explore .
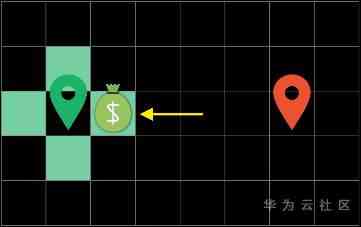
there “ cost ” That's interesting , It's also A* Where algorithms are smart .
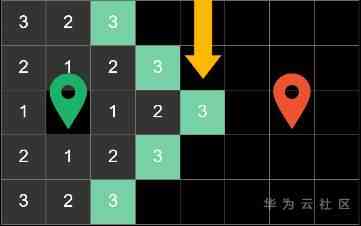
We can divide the cost here into two parts , Part of it is “ The cost of the current journey ( It can be expressed as f-cost)”: For example, how many squares do you walk through from the starting point ,f-cost Just a few .
The other part is “ Estimate the cost ( It can be expressed as g-cost)”: Used to indicate how many steps it takes to move from the current block to the final square , Estimate, estimate, so it's not an exact number , It doesn't mean that starting from the current position will definitely go that far , However, we will use this estimation to guide the algorithm to search for more promising paths first .
Most commonly used “ Estimate the cost ” There is Euler distance (Euler Distance)“, It's the linear distance between two points (x1 - x2)^2 + (y1 - y2)^2
And, of course, there's something easier to calculate “ Manhattan distance (Manhattan Distance)”, It's the sum of the vertical and horizontal distances between the two points |x1 - x2|+|y1 - y 2|
Manhattan distance does not need to square , Fast , So in A* In the algorithm, we can use it as g-cost.
Next , All we have to do is add the two costs mentioned before to get the total cost :f-cost + g-cost.
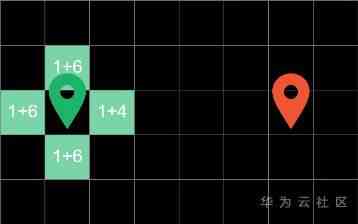
And then in the explore box , Choose the block with the lowest total cost to explore , In this way, we will take fewer detours
And the search path must be the shortest path .
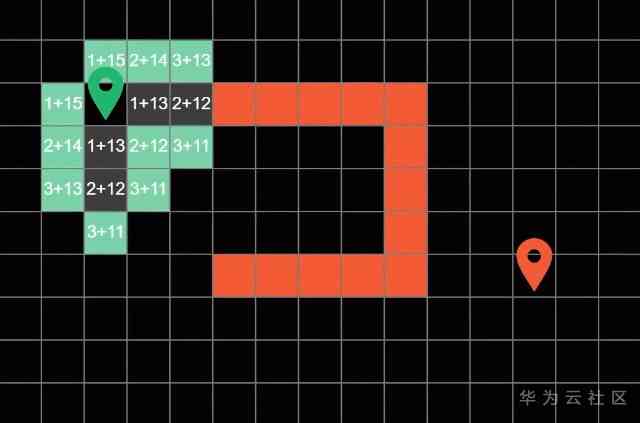
In the first cycle , The algorithm explores the four squares around the starting point , And calculate “ The current cost ” and “ Estimate the cost ”.
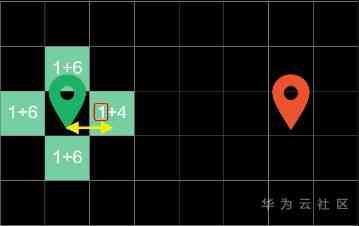
Like here 1 From the beginning to the current block has gone 1 Step
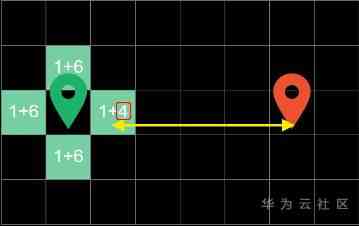
there 4 Represents the Manhattan distance from the square to the end , In these four boundary blocks , The right square costs the least , So in the next cycle, it will be searched first
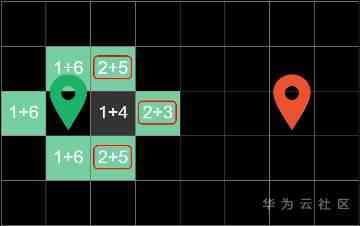
In the next cycle , We have calculated the price of the block in the same way , The lowest value of the square on the right is still found , So in the next cycle , We search for it
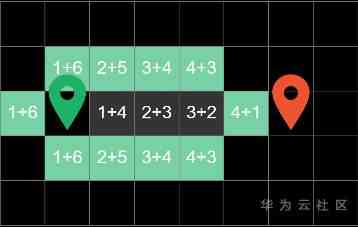
The algorithm goes on and on like this , Until the end of the search
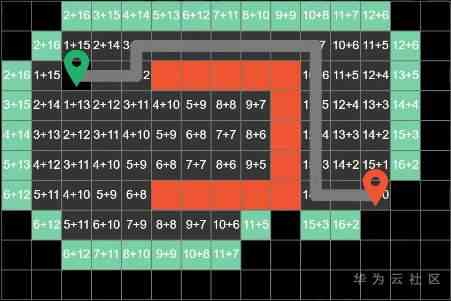
Increase the order of magnitude of the squares ,A* The algorithm can also find the right shortest path
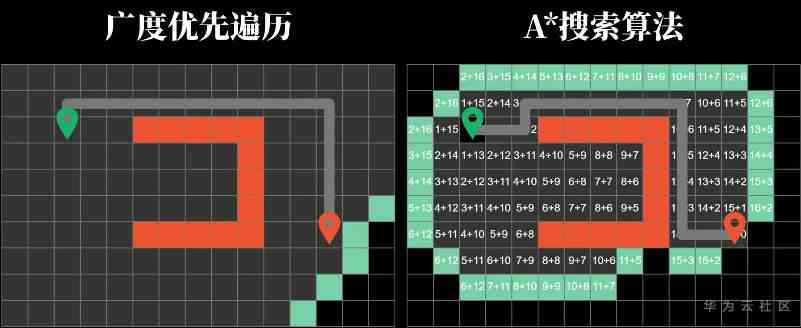
The most important thing is , The number of blocks it searches for is significantly less than that of breadth first traversal , So it's more efficient .
After understanding the basic principle of the algorithm , Next is the code , Here I quote directly redblobgames Of Python Code implementation , Because it's really good !
def heuristic(a, b): #Manhattan Distance (x1, y1) = a (x2, y2) = b return abs(x1 - x2) + abs(y1 - y2) def a_star_search(graph, start, goal): frontier = PriorityQueue() frontier.put(start, 0) came_from = {} cost_so_far = {} came_from[start] = None cost_so_far[start] = 0 while not frontier.empty(): current = frontier.get() if current = goal: break for next in graph.neighbors(current): new_cost = cost_so_far[current] + graph.cost(current, next) if next not in cost_so_far or new_cost < cost_so_far[next]: cost_so_far[next] = new_cost priority = new_cost + heuristic(goal, next) frontier.put(next, priority) came_from[next] = current return came_from, cost_so_far
Let's take a look at the top lines first ,frontier Contains all the border blocks we've explored in this round ( The green squares in the previous picture )
frontier = PriorityQueue()
PriorityQueue Represents that it is a priority queue , That means it can use “ cost ” Automatic sorting , And take it out every time ” cost “ The lowest square
frontier.put(start, 0)
In the queue, we first store an element , That's where we start
came_from = {}
The following came_from It's a map from the current block to the previous one , Represents the direction of the path
cost_so_far = {}
there cost_so_far Representing the square “ The current cost ”
came_from[start] = None cost_so_far[start] = 0
These two lines will start with came_from empty , And set the current cost of the starting point to 0, In this way, the validity of the algorithm data can be guaranteed
while not frontier.empty(): current = frontier.get()
Next , as long as frontier This queue is not empty , The cycle will continue , Every cycle , The algorithm extracts the least expensive block from the priority queue
if current = goal: break
Then check whether the block is the end block , If it's the end of the algorithm , Otherwise, go ahead
for next in graph.neighbors(current):
Next , The algorithm will check the adjacent blocks on the top, bottom, left and right of this block , That's in the loop next Show the box to do the following operations
new_cost = cost_so_far[current] + graph.cost(current, next)
The algorithm will calculate this first next square “ New cost ”, It's equal to the cost before Plus from current To next The price of the block
Because we use grids , So the second half is 1
if next not in cost_so_far or new_cost < cost_so_far[next]:
And then just next Blocks have not been detected , perhaps next The current cost is lower than before
frontier.put(next, priority)
We just put him in the priority queue , And the total cost here priority be equal to “ The current cost ” add ” Estimate the cost “
priority = new_cost + heuristic(goal, next)
The estimated cost is what I mentioned earlier “ Manhattan distance ”
def heuristic(a, b): (x1, y1) = a (x2, y2) = b return abs(x1 - x2) + abs(y1 - y2)
Then the program goes to the next loop , Repeat all the previous steps
This program is really cleverly written , It may be difficult to understand, but if you look at it more than once, you may suddenly have a bright light
expand

If you expand the map to grid form (Grid), Because there are too many nodes in the graph , Traversal can be very inefficient
So we can simplify the grid map to Signposts with fewer nodes (WayPoints)
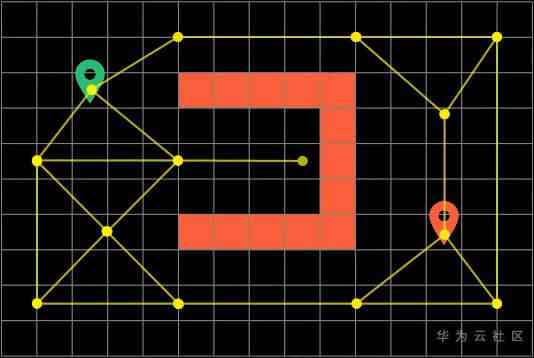
And then it's important to note that : Here, the distance between any two nodes is no longer 1 了 , It's the actual distance between nodes
We can also store maps hierarchically from top to bottom
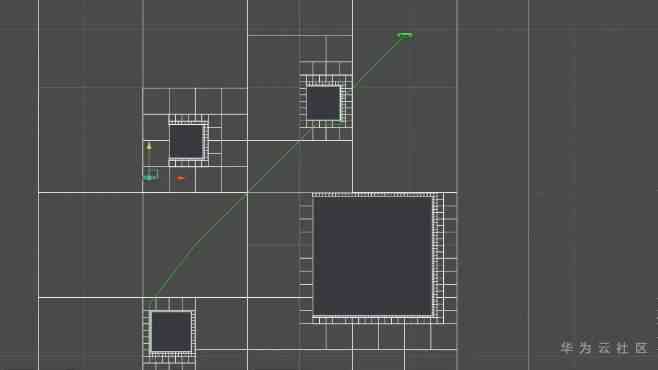
Like this quadtree (Quad Tree)
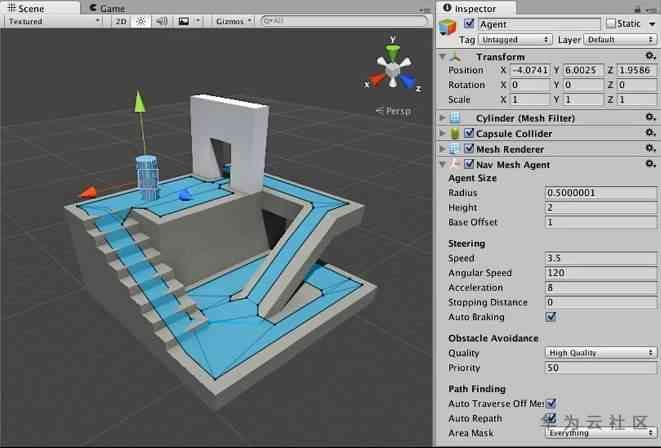
Or like unity Navigation triangulation used in (Navigation Mesh), In this way, the speed of sub algorithm will be further optimized
in addition , I also recommend redblobgames A tutorial for
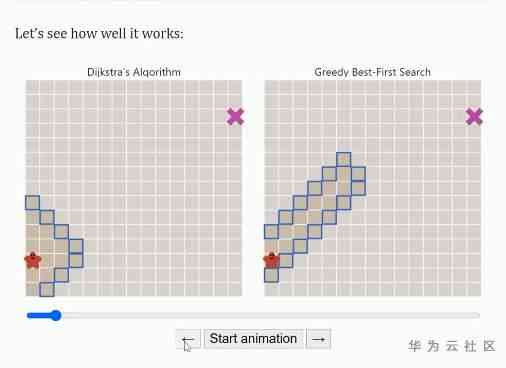
Visualization of various algorithms , And clearly see the traversal process of various algorithms 、 In the middle
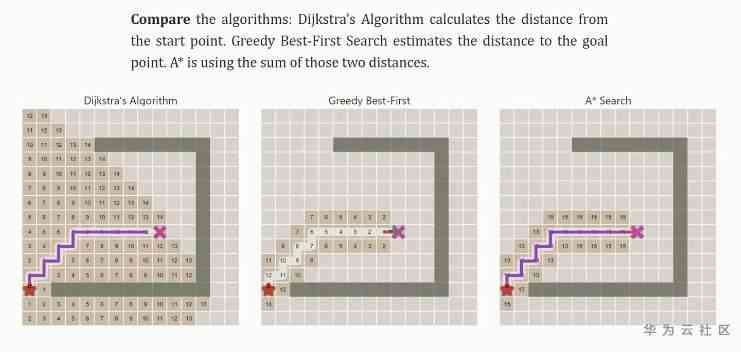
And the comparison between various methods , It's very intuitive , It's also helpful to understand the algorithm .
Reference resources :
[1] Zhou Xiaojing . Based on improvement A Algorithm of game map pathfinding research [D]. Southwest University ,2010.
[2]https://www.redblobgames.com/pathfinding/a-star/introduction.html
[3]https://en.wikipedia.org/wiki/A_search_algorithm
Click to follow , The first time to learn about Huawei's new cloud technology ~