当前位置:网站首页>[2022 广东省赛M] 拉格朗日插值 (多元函数极值 分治NTT)
[2022 广东省赛M] 拉格朗日插值 (多元函数极值 分治NTT)
2022-07-06 08:15:00 【凌乱之风】
题意
求在满足 ∑ i = 1 k x i 2 a i 2 = 1 \sum\limits_{i = 1} ^ {k}\dfrac{x_i ^ 2}{a_i ^ 2} = 1 i=1∑kai2xi2=1 的条件下,从长度为 m m m 的数组 b b b 中选 k k k 个数组成 a 1 , a 2 , ⋯ , a k a_1,a_2,\cdots,a_k a1,a2,⋯,ak, ∏ i = 1 k x i \prod\limits_{i = 1} ^{k} x_i i=1∏kxi 的最大值的期望, k k k 为偶数。
( 1 ≤ k ≤ m ≤ 1 0 5 , 0 < b i < 1 0 9 ) (1 \le k \le m \le 10 ^ 5, 0 < b_i < 10 ^ 9) (1≤k≤m≤105,0<bi<109)
分析:
首先求解最大值需要用到高等数学中多元函数条件极值的拉格朗日乘数法,设
L ( x 1 , x 2 , ⋯ , x k , λ ) = ∏ i = 1 k x i + λ ( ∑ i = 1 k x i 2 a i 2 − 1 ) L(x_1,x_2,\cdots,x_k, \lambda) = \prod_{i = 1} ^{k} x_i + \lambda(\sum\limits_{i = 1} ^ {k}\dfrac{x_i ^ 2}{a_i ^ 2} - 1) L(x1,x2,⋯,xk,λ)=i=1∏kxi+λ(i=1∑kai2xi2−1)
对每个变量求偏导数,令偏导数为 0 0 0 得
∂ L ∂ x 1 = ∏ i = 1 k x i x 1 + 2 λ x 1 a 1 2 = 0 ∂ L ∂ x 2 = ∏ i = 1 k x i x 2 + 2 λ x 2 a 2 2 = 0 ⋯ ∂ L ∂ x k = ∏ i = 1 k x i x k + 2 λ x k a k 2 = 0 ∂ L ∂ λ = ∑ i = 1 k x i 2 a i 2 − 1 = 0 \frac{\partial L}{\partial x_1} = \frac{\prod\limits_{i = 1} ^{k} x_i}{x_1} + \frac{2\lambda x_1}{a_1 ^ 2} = 0 \\ \frac{\partial L}{\partial x_2} = \frac{\prod\limits_{i = 1} ^{k} x_i}{x_2} + \frac{2\lambda x_2}{a_2 ^ 2} = 0 \\ \cdots \\ \frac{\partial L}{\partial x_k} = \frac{\prod\limits_{i = 1} ^{k} x_i}{x_k} + \frac{2\lambda x_k}{a_k ^ 2} = 0 \\ \frac{\partial L}{\partial \lambda} = \sum_{i = 1} ^ {k}\dfrac{x_i ^ 2}{a_i ^ 2} - 1 = 0 ∂x1∂L=x1i=1∏kxi+a122λx1=0∂x2∂L=x2i=1∏kxi+a222λx2=0⋯∂xk∂L=xki=1∏kxi+ak22λxk=0∂λ∂L=i=1∑kai2xi2−1=0
那么稍微化简一下,对于 1 ≤ i ≤ k 1 \le i \le k 1≤i≤k 都有
∏ i = 1 k x i = − 2 λ x i 2 a i 2 \prod_{i = 1} ^ {k}x_i = \frac{-2\lambda x_i ^ 2}{a_i ^ 2} i=1∏kxi=ai2−2λxi2
通过任意两式 1 ≤ i , j ≤ k 1 \le i, j \le k 1≤i,j≤k 联立消掉 λ \lambda λ
a i 2 ∏ i = 1 k x i − 2 x i 2 = a j 2 ∏ i = 1 k x i − 2 x j 2 \frac{a_i ^ 2\prod\limits_{i = 1} ^ {k}x_i}{-2x_i ^ 2} = \frac{a_j ^ 2\prod\limits_{i = 1} ^ {k}x_i}{-2x_j ^ 2} −2xi2ai2i=1∏kxi=−2xj2aj2i=1∏kxi
化简得
x i a i = x j a j \frac{x_i}{a_i} = \frac{x_j}{a_j} aixi=ajxj
所以当且仅当 x 1 a 1 = x 2 a 2 = ⋯ = x k a k \dfrac{x_1}{a_1} = \dfrac{x_2}{a_2}=\cdots=\dfrac{x_k}{a_k} a1x1=a2x2=⋯=akxk 时取得最大值,且 ∑ i = 1 k x i 2 a i 2 = 1 \sum\limits_{i = 1} ^ {k}\dfrac{x_i ^ 2}{a_i ^ 2} = 1 i=1∑kai2xi2=1,所以对任意 1 ≤ i ≤ k 1 \le i \le k 1≤i≤k 都有 x i a i = ± 1 k \dfrac{x_i}{a_i} = \pm \sqrt{\dfrac{1}{k}} aixi=±k1,那么 ∏ i = 1 k x i = k − k 2 ∏ i = 1 k a i \prod\limits_{i = 1} ^{k} x_i = k ^ {- \frac{k}{2}}\prod\limits_{i = 1} ^ {k} a_i i=1∏kxi=k−2ki=1∏kai,因为 k k k 为偶数,所以一定为正,且 k 2 \dfrac{k}{2} 2k 一定是整数。
求从 b b b 数组中选出 k k k 个数的所有乘积之和,考虑构造生成函数
F ( x ) = ∏ i = 1 k ( 1 + b i x ) F(x) = \prod_{i = 1} ^ {k} (1 + b_ix) F(x)=i=1∏k(1+bix)
那么 [ x k ] F ( x ) [x ^ k]F(x) [xk]F(x) 就是选出 k k k 个数的所有乘积之和,总共有 ( m k ) \dbinom{m}{k} (km) 种选法,所以期望就为
k − k 2 × [ x k ] F ( x ) ( m k ) k ^ {-\frac{k}{2}} \times \frac{[x ^ k]F(x)}{\dbinom{m}{k}} k−2k×(km)[xk]F(x)
F ( x ) F(x) F(x) 可用分治 NTT \text{NTT} NTT 计算,总时间复杂度 O ( n log 2 n ) O(n\log ^ 2n) O(nlog2n)
代码:
#include <bits/stdc++.h>
#define int long long
#define poly vector<int>
#define len(x) ((int)x.size())
using namespace std;
const int N = 3e5 + 5, G = 3, Ginv = 332748118, mod = 998244353;
int rev[N], lim;
int qmi(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res;
}
void polyinit(int n) {
for (lim = 1; lim < n; lim <<= 1);
for (int i = 0; i < lim; i ++) rev[i] = (rev[i >> 1] >> 1) | (i & 1 ? lim >> 1 : 0);
}
void NTT(poly &f, int op) {
for (int i = 0; i < lim; i ++) {
if (i < rev[i]) swap(f[i], f[rev[i]]);
}
for (int mid = 1; mid < lim; mid <<= 1) {
int Gn = qmi(op == 1 ? G : Ginv, (mod - 1) / (mid << 1));
for (int i = 0; i < lim; i += mid * 2) {
for (int j = 0, G0 = 1; j < mid; j ++, G0 = G0 * Gn % mod) {
int x = f[i + j], y = G0 * f[i + j + mid] % mod;
f[i + j] = (x + y) % mod, f[i + j + mid] = (x - y + mod) % mod;
}
}
}
if (op == -1) {
int inv = qmi(lim, mod - 2);
for (int i = 0; i < lim; i ++) f[i] = f[i] * inv % mod;
}
}
poly operator * (poly f, poly g) {
int n = len(f) + len(g) - 1;
polyinit(n), f.resize(lim), g.resize(lim);
NTT(f, 1), NTT(g, 1);
for (int i = 0; i < lim; i ++) f[i] = f[i] * g[i] % mod;
NTT(f, -1), f.resize(n);
return f;
}
vector<int> fact, infact;
void init(int n) {
fact.resize(n + 1), infact.resize(n + 1);
fact[0] = infact[0] = 1;
for (int i = 1; i <= n; i ++) {
fact[i] = fact[i - 1] * i % mod;
}
infact[n] = qmi(fact[n], mod - 2);
for (int i = n; i; i --) {
infact[i - 1] = infact[i] * i % mod;
}
}
int C(int n, int m) {
if (n < 0 || m < 0 || n < m) return 0ll;
return fact[n] * infact[n - m] % mod * infact[m] % mod;
}
signed main() {
cin.tie(0) -> sync_with_stdio(0);
init(1e5);
int n, k;
cin >> n >> k;
vector<int> b(n + 1);
vector<poly> f(n + 1, poly(2));
for (int i = 1; i <= n; i ++) {
cin >> b[i];
f[i][0] = 1, f[i][1] = b[i];
}
function<poly(int, int)> dc = [&](int l, int r) {
if (l == r) return f[l];
int mid = l + r >> 1;
return dc(l, mid) * dc(mid + 1, r);
};
poly ans = dc(1, n);
int res = 1;
cout << qmi(qmi(k, k / 2), mod - 2) * ans[k] % mod * qmi(C(n, k), mod - 2) % mod << endl;
}
边栏推荐
- Day29-t77 & t1726-2022-02-13-don't answer by yourself
- National economic information center "APEC industry +": economic data released at the night of the Spring Festival | observation of stable strategy industry fund
- "Designer universe" Guangdong responds to the opinions of the national development and Reform Commission. Primary school students incarnate as small community designers | national economic and Informa
- Introduction to number theory (greatest common divisor, prime sieve, inverse element)
- [Yugong series] creation of 009 unity object of U3D full stack class in February 2022
- MFC sends left click, double click, and right click messages to list controls
- Understanding of law of large numbers and central limit theorem
- Yyds dry goods inventory three JS source code interpretation eventdispatcher
- ESP系列引脚说明图汇总
- CAD ARX gets the current viewport settings
猜你喜欢
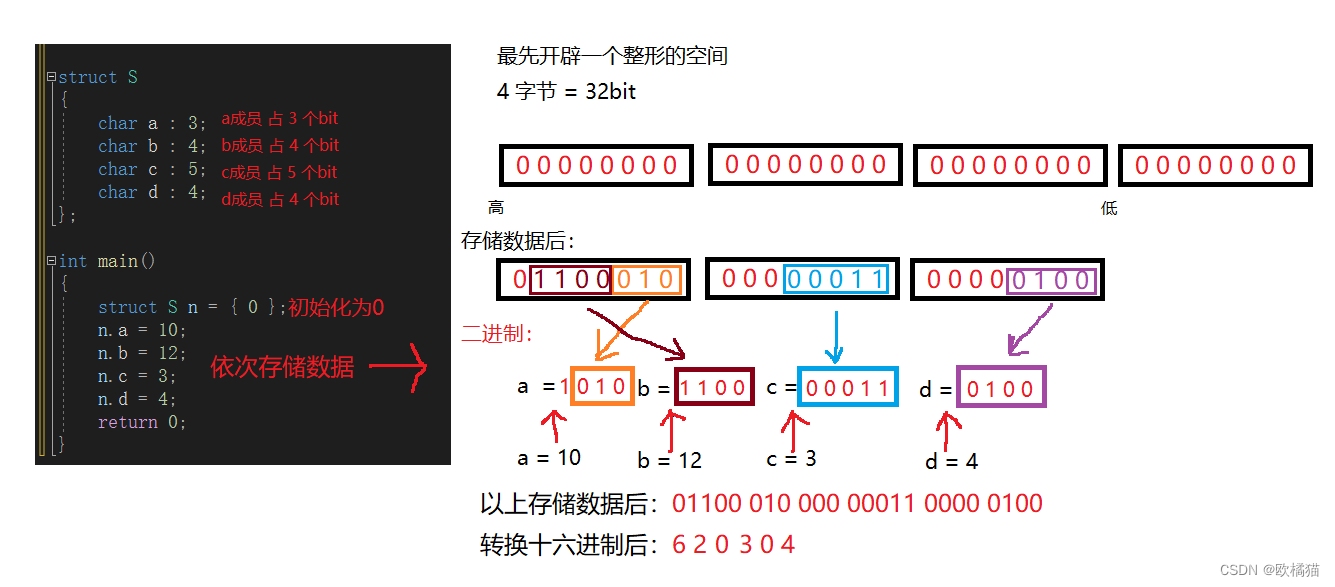
C语言 - 位段
![[Yugong series] February 2022 U3D full stack class 011 unity section 1 mind map](/img/c3/1b6013bfb2441219bf621c3f0726ea.jpg)
[Yugong series] February 2022 U3D full stack class 011 unity section 1 mind map

化不掉的钟薛高,逃不出网红产品的生命周期

The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
![[research materials] 2022 China yuancosmos white paper - Download attached](/img/b4/422dff0510bbe67f3578202d6e80b7.jpg)
[research materials] 2022 China yuancosmos white paper - Download attached

. Net 6 learning notes: what is NET Core

The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
![[research materials] 2021 China online high growth white paper - Download attached](/img/51/bea6179e4fac88f8b550b4213a2bca.jpg)
[research materials] 2021 China online high growth white paper - Download attached
![[research materials] 2021 Research Report on China's smart medical industry - Download attached](/img/c8/a205ddc2835c87efa38808cf31f59e.jpg)
[research materials] 2021 Research Report on China's smart medical industry - Download attached
2.10transfrom attribute
随机推荐
Use br to back up tidb cluster data to S3 compatible storage
What are the ways to download network pictures with PHP
C语言自定义类型:结构体
The State Economic Information Center "APEC industry +" Western Silicon Valley will invest 2trillion yuan in Chengdu Chongqing economic circle, which will surpass the observation of Shanghai | stable
华为云OBS文件上传下载工具类
Codeforces Global Round 19(A~D)
Convolution, pooling, activation function, initialization, normalization, regularization, learning rate - Summary of deep learning foundation
synchronized 解决共享带来的问题
"Designer universe": "benefit dimension" APEC public welfare + 2022 the latest slogan and the new platform will be launched soon | Asia Pacific Financial Media
Analysis of pointer and array written test questions
Restore backup data on S3 compatible storage with br
数据治理:微服务架构下的数据治理
Migrate data from CSV files to tidb
File upload of DVWA range
MySQL view tablespace and create table statements
CAD ARX gets the current viewport settings
将 NFT 设置为 ENS 个人资料头像的分步指南
Hill sort c language
数据治理:数据质量篇
. Net 6 learning notes: what is NET Core