Convolution, pooling, activation function, initialization, normalization, regularization, learning rate - Summary of deep learning foundation

I have the honor to read the book of big brother Yan Yousan 《 The model design of deep learning 》, Here are my reading notes , For reference only , You have to read the original work for details , Please correct the mistakes . The following three pictures are from Zhihu .

《 The model design of deep learning 》 Reading notes —— Chapter two ： The foundation of deep learning

2.1 Limitations of fully connected neural networks

2.2.1 Defects of learning principles

  Traditional machine learning requires artificial design of feature description operators , But people are limited after all , This limits the expression ability of the traditional fully connected neural network in principle , It can only solve relatively simple problems .

2.2.2 Structural defects of fully connected neural networks

• Huge amount of calculation
• Lack of structural information

2.2.3 High performance traditional machine learning algorithm

• Adaboost
• SVM

2.2 Study the brief history of the third Renaissance in depth

2.2.1 The Internet and big data are coming

  The birth of large data sets , Many machine learning models have enough data to train models with good generalization performance .

2.2.2GPU The popularity of

1. What is? GPU

• Definition ：GPU(Graphics Processing Unit) Graphics processor .
• characteristic ：GPU Using a large number of computing units and ultra long pipeline , And it saves Cache.

2.GPU Architecture and software platform
 GPU Programmable .
 GPU Development stage ： Fixed function architecture stage $\Rightarrow$ Separate the rendering architecture stage $\Rightarrow$ Unified rendering architecture stage

3.GPU And CPU Computational power comparison
 (1)GPU The floating-point operation ability of is CPU More than ten times .
 (2)GPU It has high-speed and wide independent video memory ; High floating point performance ; Strong geometric processing ability ; Suitable for processing parallel computing tasks ; Suitable for repeated calculation ; Suitable for image or video processing tasks ; It can greatly reduce the system cost .

2.2.3 The deep neural network is gorgeous

A little

2.2.4 A major breakthrough in speech recognition

A little

2.2.5 A major breakthrough in image recognition

ZFNet( deconvolution )(2013)$\Rightarrow$GoogLeNet(Inception)&VGGNet(2014)$\Rightarrow$ResNet(2015)$\Rightarrow$ResNeXt( Grouping convolution )&DenseNet(2016)$\Rightarrow$SeNet(2017)

2.2.6 A major breakthrough in natural language processing

LSTM(2014)$\Rightarrow$ Attention mechanism (2014)$\Rightarrow$Transformer(2017)$\Rightarrow$ELMO(2017)$\Rightarrow$GPT(2018)$\Rightarrow$GPT2.0(2019)$\Rightarrow$XLNet(2019)

2.3 The basis of convolutional neural network

2.3.1 Convolution operation

1. Mathematical convolution ：

among $(x\ast w)(t)$ be called $x$ and $w$ Convolution of
Continuous definition ：$(x\ast w)(t)={\int }_{-\infty }^{+\infty }f(\tau )g(t-\tau )d\tau$
The definition of discreteness ：$(x\ast w)(t)={\sum }_{-\infty }^{+\infty }f(\tau )g(t-\tau )$

2. Convolution of two-dimensional graphics ：

$$(x\ast w)(i,j)=\sum _m\sum _{n}x(m,n)w(i-m,j-n)$$

among $x$ Indicates input $w$ Convolution kernel .
To put it bluntly , Convolution is sliding on the image , Take a region equal in size to the convolution kernel , Multiply pixel by pixel and add .
I add ： There are also three modes in convolution ：
1.full mode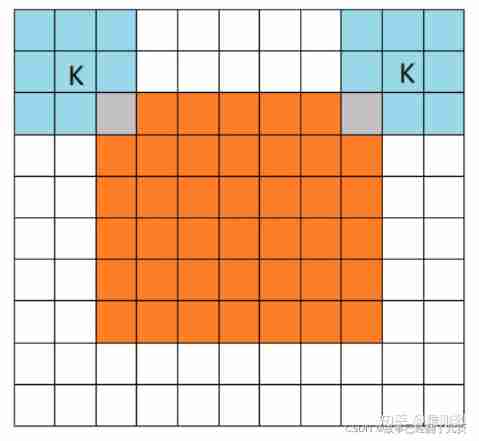

full The pattern means , from filter and image Just started convolution , The white part is filled with 0.filter The range of motion is shown in the figure .
2.same mode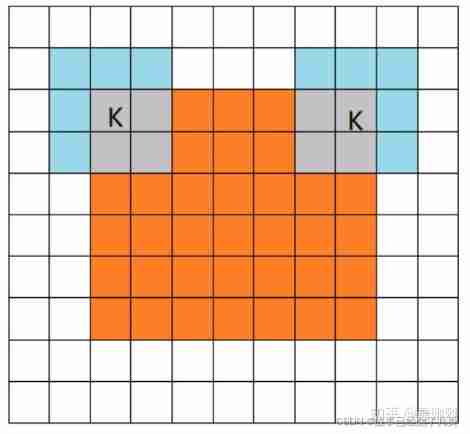

When filter Center of (K) And image When the edges and corners coincide , Start convolution , so filter The range of motion is larger than full The pattern is a little smaller . Be careful ： there same There is another meaning , Output after convolution feature map The size remains the same ( Relative to the input picture ). Of course ,same Mode does not mean that the input and output dimensions are the same , It also has something to do with the step size of the convolution kernel .same Patterns are also the most common patterns , Because this mode can keep the size of the feature graph unchanged in the process of forward propagation , The parameter adjuster does not need to accurately calculate its size change ( Because the size hasn't changed at all ).
3.valid mode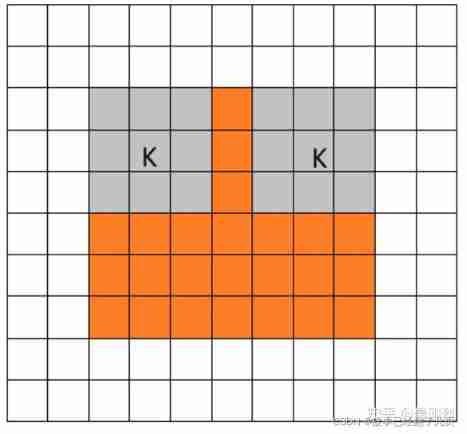

When filter All in image When it's inside , Do convolution , so filter The moving range of the is same Smaller .

2.3.2 Deconvolution operation

Convolution usually causes resolution reduction , Deconvolution is just the opposite .
actually , There is no such operation as deconvolution , Currently in DeepLearning There are mainly two ways to realize deconvolution —— Interpolation and transpose convolution

1. Interpolation method

Four points are known $Q_{11}=(x_1,y_1),Q_{12}=(x_1,y_2),Q_{21}=(x_2,y_1),Q_{22}=(x_2,y_2)$
Yes $x$ Linear difference in direction :
$f(x,y_1)\approx \frac{x_2-x}{x_2-x_1}f(Q_{11})+\frac{x-x_1}{x_2-x_1}f(Q_{21})$
$f(x,y_2)\approx \frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22})$
Then on $y$ Linear difference in direction ：
$f(x,y)\approx \frac{y_2-y}{y_2-y_1}f(x,y_1)+\frac{y-y_1}{y_2-y_1}f(x,y_2)$
First pair y The direction is again right x The result of directional interpolation is the same .

2. Transposition convolution ( deconvolution )

In fact, it is also a convolution operation , Use the same code as convolution .
In practice , First calculate Up sampling magnification ($\frac{transportOutruler"}{transportEnter\; intoruler"}$). According to Step Size and Boundary supplement To transform the initial input . Then use the same method as convolution to learn parameters .

2.3.3 Basic concept of convolutional neural network

1. Feel the field

stay CNN in , It is a mapping of the input layer corresponding to an element of the output result of a certain layer , That is, the area on the input image corresponding to a point on the feature plane .
If the size of a neuron is affected by the upper layer $N\times N$ The influence of neuronal regions , So the receptive field of this neuron is $N\times N$, Because it reacts $N\times N$ Regional information .

2. Pooling

Realization way :

1. step Not for 1 Convolution of ;
2. Direct sampling .

The pooling layer can compress the input feature plane , Sure ：

1. Make the feature plane smaller , Simplify network computing complexity ;
2. Extract the main features .

Common pooling is ：

Average Pooling、Max Pooling.

2.3.4 The core idea of convolutional neural network

1. Sparse connection

Most of the neurons in the anterior and posterior layers are connected locally .
The source of thought ： Physiological receptive field mechanism and Local statistical properties of images

2. Weight sharing

Weight sharing in the same feature plane .
The information learned in the local area of the image can be applied to other areas , So that the same target can extract the same features in different positions .

3. Can model image structure information

The preservation of spatial relations is CNN The basis for extracting robust features

2.3.5 CNN Basic structure configuration of

• Input layer ： Contains basic operations ： If you go to the mean value , Gray normalization
• Convolution layer
• Activation layer ： Select and suppress features
• Pooling layer ： Reduce the resolution and abstract features of the plane ; Compress network parameters and data , Reduce over fitting
• Fully connected layer
• Loss layer ; Define the loss objective function ( Such as SGD), Find the parameter value of the minimization loss function （ The input of the loss layer is the output of the network and the real label ）
• Precision layer ： The input is the output of the network and the real label

2.4.1 Activation model and common activation functions

1. Linear model and threshold model

2. Activation function

• Sigmoid: $f(x)=\frac{1}{1+e^{-x}}$
• Tanh: $f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$ It's solved Sigmoid The output value of the function does not begin with 0 Centered problem
• ReLU
• Leaky ReLU：$f(x)=max(0.01x,x)$, It's solved Dead ReLU problem , But it has not been completely proved to be better than ReLU
• PreLU： take Leaky ReLU Medium $\alpha$ Set as a parameter that can be learned
• Maxout：$y=max(a_k)=max(w_1^{T}x+b_1,w_2^{T}x+b_2,...,w_n^{T}x+b_n)$ Consider adding an activation function layer to the network , It contains a parameter k, The special thing is that k Neurons , And output the maximum activation value .
  have ReLU All the advantages of functions , There are no shortcomings .
  Can fit any convex function .
  and Dropout The combined use effect is better .
• Softmax：$f(x_1)=\frac{e^{x_i}}{{\sum }_{k=1}^K{e}^{x_k}}$ As Sigmoid The generalized form of .
• Swish：$f(x)=x\ast Sigmoid(\beta x)$ , It is an activation function automatically searched by the network , among $\beta$ Is a parameter or constant that can be learned .

3. Research direction of activation function

1. Yes ReLU Improve the negative region of the function
2. Study different activation strategies for different network layers 、 The impact of different channel use
3. Use various learning methods to explore simple combinations
at present ,ReLU Functions are still the most common .

2.4.2 Parameter initialization method

principle ：

• The activation value of each layer will not be saturated
• The activation value of each layer is not 0

Ideal initialization ： Make the activation value of each layer consistent with the variance of the state gradient in the propagation process

1. Initialize to 0

Not conducive to optimization

2. Generate small random numbers

Gaussian distribution can be used
The initial value of the parameter cannot be too small ： Smaller parameters will cause too small gradients when propagating , For deep Networks , Will produce gradient dispersion .
The initial value of the parameter cannot be too large ： Cause oscillation , Also can make Sigmoid Enter the gradient saturation zone .

3. Standard initialization

4.Xavier initialization

5.MSRA initialization

6. Use of initialization methods

• Use a trained model （ The best initialization method ）
• Choose a better activation function ：
  MSRA Initialization method +ReLU Series collocation —— The current mainstream

2.4.3 Normalization method

Definition ： Normalization is to constrain data to a fixed distribution range .

1.Normalization

• Linear contrast stretch ：$X=\frac{x-x_{min}}{x-x_{max}}$ , among $x_{min}$ and $x_{max}$ They are the minimum and maximum gray values .
• Histogram equalization ： Let one transform from random distribution to [0,1] Uniformly distributed transformation .
  
  Transformation steps ：
  
  （1） Calculate cumulative probability distribution ,$cdp(r_k)$ Indicates that the gray scale is $0-r_k$ The probability of pixels .$cdp(L-1)=1$. $cdp(r_k)={\sum }_{i=0}^{L-1}p(r_k),k=0,1,2...L-1$
  
  （2） Create a uniform distribution , Convert the cumulative probability distribution to the pixel range of the image , The transformation relation is ：$T(r_k)=round(cdp(r_k)\ast 255+0.5)$, among $round$ Indicates rounding operation .$T(r_k)$ stay $(0,255)Inside$
  
  （3） Reverse mapping , New pixel gray value after transformation $y$ With the original pixel gray value $x$ The transformation relation of is $y=T(x)$
• Zero mean normalization ： The average value of the processed data is 0, The standard deviation is 1 The standard normal distribution of .$y_i=\frac{x_i-u}{\delta }$

2.Batch Normalization

Usually BN The layer is behind the convolution layer , Used to redistribute data .

ensp Average value of each batch ：$u_B=\frac{1}{n}{\sum }_{i=1}^n{x}_i$

Variance of each batch ：$\delta^2_B = \dfrac{1}{n} \sum^n_{i=1} (x_i-u_B)^2 $

Normalize each element ：$x_i^{{}^{\prime }}=\frac{x_i-u_B}{\sqrt{{\delta }_B^2+\epsilon }}$

Scaling and shifting ：$y_i={\gamma }_i\times x_i^{{}^{\prime }}+{\beta }_i$, among ,$\gamma$ and $\beta$ Represents the variance and offset of the input data distribution .

CNN Each characteristic dimension of （ passageway ） Between , It is conducted separately BN Calculated .
BN The benefits of ：1. Reduce the dependence on the initial value 2. Faster training , You can use a higher learning rate
BN The shortcomings of ： rely on Batch Size , When Batch It's worth a lot of time , The calculated mean and variance are unstable . Therefore, it is not suitable for 1.Batch A very small 2. A model with variable depth , Such as RNN

3.Batch Renormalization

BN With each Batch To replace the mean and variance of the overall training set , This requires Batch Samples must be taken evenly from all types , When Batch When the value is small, it is difficult to meet this requirement .
and Batch Renormalization And then we can solve this problem .
take BN Change the corresponding formula in ：
$x_i^{{}^{\prime }}=\frac{x_i-u_B}{{\delta }_{\beta }}.r+d$

among $r=\frac{{\delta }_{\beta }}{\delta }$, $d=\frac{u_{\beta }-u}{\delta }$

among $u:=u+\alpha (u_{\beta }-u)$,$\delta :=\delta +\alpha (u_{\beta }-\delta )$

In practice , First use BN Train the network to a relatively stable moving average , Reuse Batch Renormalization Training .

4.BN variant

• Layer Normalization(LN)： Apply to RNN Equal time series model
• Instance Normalization(IN)： Suitable for image generation and style transfer
• Generalized Normalization(GN)： Apply to Batch smaller
• Switchable Normalization(SN): Choose from the pool containing the normalization method , And then compare the accuracy to select the best , Finally, the best configuration is learned adaptively in the task . The specific result may be ： When the batch processing is smaller ,BN The more unstable , The smaller the corresponding weight coefficient ,IN and LN The larger the weight coefficient of ; conversely BN The larger the weight coefficient of （ A bit like a random forest ）.

2.4.4 Pooling

1. Based on the scheme of manually designing pooling

• Average Pooling
• Max Pooling
• Mixed Pooling： stay Average Pooling and Max Pooling Random selection in , It can provide certain regularization ability
• Stochastic Pooling： Yes feature map The elements in are randomly selected according to the size of the probability value , The probability of an element being selected is positively correlated with its value .

2. Data driven pooling scheme

Under study

3. Understanding of pooling mechanism

effect ： Translation invariance is increased to a certain extent
It doesn't play a big role in the deep network , What is really useful is data enhancement .

2.4.5 Optimization method —— Optimizer

• SGD(Stochastic Gradient Descent)： Only one sample is selected at a time for gradient calculation
• RMSProp
• AdaGrad
• NAG(Nesterov Accelerated Gradient)
• Adam: It's essentially a momentum term REMSProp
• Adamax： The upper limit of learning rate provides a simpler range
• Nadam： with Nesterov Of momentum terms Adam
• Newton method
• Quasi Newton method
• conjugate gradient method

2.4.6 Learning rate strategy

The more late in training , The lower the learning rate , Contribute to the stability of convergence

• Fixed： Fixed learning rate strategy
• Step： Adjust the learning rate according to the specified step . Such as ： Learning rate every time 10000 After the second iteration, it is reduced to the original 0.1 times
• Multistep： Non uniform step size reduction strategy
• Exp： Index change strategy
• Inv： Another index change strategy
• Poly： Another index change strategy
• Sigmoid

2.4.7 Regularization method

1. Over fitting and under fitting

• Over fitting (Overfitting)： The data set is very small or The model is too big —— resolvent ： Regularization and data expansion
• Under fitting (Underfitting)： Not trained enough

2. Regularization

• Regularization (Regularization)： The goal is ： Let experience risk and model complexity be smaller at the same time . effect ： The generalization error is reduced by increasing the error of the training set .

3. Early stop

After the verification error no longer increases , Finish training early
Strategies for making full use of training data sets ：1. Train all training data together for a fixed number of iterations 2. Iterative training process , Until the training error is less than the verification error of the early stop strategy setting .

4. Model integration

• Model Ensemble Methods: Combine the results of multiple models to get a better model
• dropout

5. Parameter penalty

6. Training sample expansion

• CV in ： Rotate the picture 、 The zoom 、 Translation, etc
• NLP in ： Synonym replacement, etc
• In speech recognition ： Add random noise, etc