当前位置:网站首页>傅里叶级数
傅里叶级数
2022-07-02 03:26:00 【Zeehoy】
傅里叶级数理论:周期为 2 π 2π 2π 的周期函数 f ( x ) f(x) f(x) ,可以写作一系列三角函数的线性组合:
f ( x ) = a 0 c o s 0 + b 0 s i n 0 + a 1 c o s x + b 1 s i n x + a 2 c o s 2 x + b 2 s i n 2 x + . . . + a n c o s n x + b n s i n n x f(x)=a_0cos0+b_0sin0+a_1cosx+b_1sinx+a_2cos2x+b_2sin2x+...+a_ncosnx+b_nsinnx f(x)=a0cos0+b0sin0+a1cosx+b1sinx+a2cos2x+b2sin2x+...+ancosnx+bnsinnx
从二维平面中,正交基谈起:
假定 a ⃗ \vec{a} a, b ⃗ \vec{b} b 相互正交,它们的线性组合可以表示平面中任意一个向量 v ⃗ \vec{v} v:
v ⃗ = n a ⃗ + m b ⃗ \vec{v}=n\vec{a}+m\vec{b} v=na+mb
对于系数 n , m n,m n,m 可以用如下方式求解:
v ⃗ ⋅ a ⃗ = n a ⃗ ⋅ a ⃗ + m b ⃗ ⋅ a ⃗ \vec{v} \cdot \vec{a}=n\vec{a}\cdot\vec{a}+m\vec{b}\cdot\vec{a} v⋅a=na⋅a+mb⋅a
由于 a ⃗ , b ⃗ \vec{a},\vec{b} a,b相互正交,所以它们点乘的结果为0:
v ⃗ ⋅ a ⃗ = n a ⃗ ⋅ a ⃗ n = v ⃗ ⋅ a ⃗ a ⃗ ⋅ a ⃗ \vec{v} \cdot \vec{a}=n\vec{a}\cdot\vec{a}\\ n=\frac{\vec{v} \cdot \vec{a}}{\vec{a}\cdot\vec{a}} v⋅a=na⋅an=a⋅av⋅a
同理:
m = v ⃗ ⋅ b ⃗ b ⃗ ⋅ b ⃗ m=\frac{\vec{v} \cdot \vec{b}}{\vec{b}\cdot\vec{b}} m=b⋅bv⋅b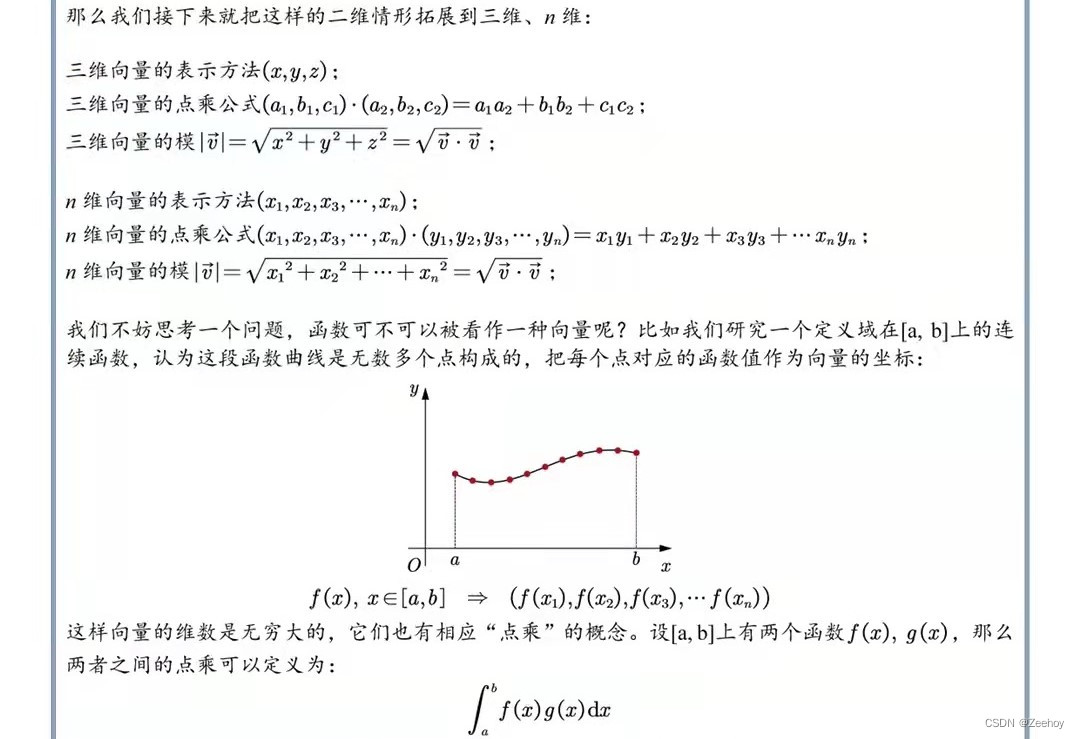
如果 ∫ a b f ( x ) g ( x ) d x = 0 \int_a^bf(x)g(x)dx=0 ∫abf(x)g(x)dx=0,即点乘的结果为0,则认为两个函数 f ( x ) f(x) f(x), g ( x ) g(x) g(x)是正交的。
与向量的正交基类似,一组函数形式的正交基的线性组合,同样可以表示相同区间的任意一个函数。
一、 [ 0 , 2 π ] [0,2π] [0,2π]
而三角函数集合: { c o s 0 , s i n 0 , c o s x , s i n x , c o s 2 x , s i n 2 x , . . . . . . , c o s n x , s i n n x } \{ {cos0,sin0,cosx,sinx,cos2x,sin2x,......,cosnx,sinnx\}} { cos0,sin0,cosx,sinx,cos2x,sin2x,......,cosnx,sinnx}中,由于任意两个不同的函数在区间 [ 0 , 2 π ] [0,2π] [0,2π] 内的点乘结果为0,每个函数与自己点乘的结果为 π π π,所以可认为是区间 [ 0 , 2 π ] [0,2π] [0,2π] 内的一组正交基。
因此,区间 [ 0 , 2 π ] [0,2π] [0,2π] 内的任意一个函数都可用这组基的线性组合表示:
f ( x ) = a 0 c o s 0 + b 0 s i n 0 + a 1 c o s x + b 1 s i n x . . . + a n c o s n x + b n s i n n x f(x)=a_0cos0+b_0sin0+a_1cosx+b_1sinx...+a_ncosnx+b_nsinnx f(x)=a0cos0+b0sin0+a1cosx+b1sinx...+ancosnx+bnsinnx
也就是文章一开始提到的傅里叶级数理论。
与上文中二维平面部分的系数求解方法类似,这里的系数同样可以类似的方式求解:
a n = ∫ 0 2 π f ( x ) c o s n x d x ∫ 0 2 π c o s n x c o s n x d x = 1 π ∫ 0 2 π f ( x ) c o s n x d x , n ∈ N a_n=\frac{\int_0^{2π}f(x)\,cosnx\,dx}{\int_0^{2π}cosnx\,cosnx\,dx}=\frac{1}{π}\int_0^{2π}f(x)cosnx\,dx,n\in N an=∫02πcosnxcosnxdx∫02πf(x)cosnxdx=π1∫02πf(x)cosnxdx,n∈N
b n = ∫ 0 2 π f ( x ) s i n n x d x ∫ 0 2 π s i n n x s i n n x d x = 1 π ∫ 0 2 π f ( x ) s i n n x d x , n ∈ N b_n=\frac{\int_0^{2π}f(x)\,sinnx\,dx}{\int_0^{2π}sinnx\,sinnx\,dx}=\frac{1}{π}\int_0^{2π}f(x)sinnx\,dx,n\in N bn=∫02πsinnxsinnxdx∫02πf(x)sinnxdx=π1∫02πf(x)sinnxdx,n∈N
式子最前面的两项:
a 0 c o s 0 + b 0 s i n 0 = a 0 c o s 0 + 0 = a 0 = ∫ 0 2 π f ( x ) c o s 0 d x ∫ 0 2 π c o s 0 c o s 0 d x = ∫ 0 2 π f ( x ) d x ∫ 0 2 π 1 d x = 1 2 π ∫ 0 2 π f ( x ) d x a_0cos0+b_0sin0=a_0cos0+0=a_0=\frac{\int_0^{2π}f(x)\,cos0\,dx}{\int_0^{2π}cos0\,cos0\,dx}=\frac{\int_0^{2π}f(x)\,dx}{\int_0^{2π}1dx}=\frac{1}{2π}\int_0^{2π}f(x)\,dx a0cos0+b0sin0=a0cos0+0=a0=∫02πcos0cos0dx∫02πf(x)cos0dx=∫02π1dx∫02πf(x)dx=2π1∫02πf(x)dx
后面部分写成累加的形式:
f ( x ) = a 0 + ∑ n = 1 + ∞ ( a n c o s n x + b n s i n n x ) f(x)=a_0+\sum_{n=1}^{+∞}(a_n\,cosnx+b_n\,sinnx) f(x)=a0+n=1∑+∞(ancosnx+bnsinnx)
二、 [ 0 , 2 l ] [0,2l] [0,2l]
一中的区间局限在 [ 0 , 2 π ] [0,2π] [0,2π],可通过伸缩的方式使区间扩展到 [ 0 , 2 l ] [0,2l] [0,2l] :
如 c o s x cosx cosx 的周期为 T = 2 π w = 2 π 1 = 2 π T=\frac{2π}{w}=\frac{2π}{1}=2π T=w2π=12π=2π 在 2 π 2π 2π 处会开始重复,想让它的周期变为 2 l 2l 2l,即在 2 l 2l 2l 处进入重复, 即 T = 2 π w = 2 l T=\frac{2π}{w}=2l T=w2π=2l,得: w = 2 π 2 l = π l w=\frac{2π}{2l}=\frac{π}{l} w=2l2π=lπ
c o s x cosx cosx 变为 c o s π l x cos \frac{π}{l}x coslπx 即可满足要求
另一方面,虽然 c o s 2 x cos2x cos2x 的周期为 π π π,但它仍会在 2 π 2π 2π 处开始重复,即 2 π 2π 2π 仍是 c o s 2 x cos2x cos2x 的一个周期,其他 c o s n x cosnx cosnx 同理
全部经过伸缩后:
{ c o s π l n x , s i n π l n x ∣ n ∈ N } \{ {cos\frac{π}{l}nx,sin\frac{π}{l}nx\,| \,n\in N\}} { coslπnx,sinlπnx∣n∈N}就同样都有一个最小公共周期 2 l 2l 2l,且由于它们仍然保持相互正交的关系,和自身的点乘结果为 l l l,因此该集合仍是一组基,此时它的线性组合可以表示 [ 0 , 2 l ] [0,2l] [0,2l] 内的任意一个函数。
f ( x ) = a 0 + ∑ n = 1 + ∞ ( a n c o s π l n x + b n s i n π l n x ) f(x)=a_0+\sum_{n=1}^{+∞}(a_n\,cos\frac{π}{l}nx+b_n\,sin\frac{π}{l}nx) f(x)=a0+n=1∑+∞(ancoslπnx+bnsinlπnx)
与一中同理, a 0 a_0 a0 是线性组合的前两项:
a 0 c o s π l 0 + b 0 s i n π l 0 = a 0 c o s 0 + b 0 s i n 0 = a 0 = ∫ 0 2 l f ( x ) c o s π l 0 d x ∫ 0 2 l c o s π l 0 c o s π l 0 d x = ∫ 0 2 l f ( x ) c o s 0 d x ∫ 0 2 l c o s 0 c o s 0 d x = 1 2 l ∫ 0 2 l f ( x ) d x a_0cos\frac{π}{l}0+b_0sin\frac{π}{l}0\\ =a_0cos0+b_0sin0\\ =a_0\\ =\frac{\int_0^{2l}f(x)\,cos\frac{π}{l}0\,dx}{\int_0^{2l}cos\frac{π}{l}0\,cos\frac{π}{l}0\,dx}\\ =\frac{\int_0^{2l}f(x)\,cos0\,dx}{\int_0^{2l}cos0\,cos0\,dx}\\ =\frac{1}{2l}\int_0^{2l}f(x)dx a0coslπ0+b0sinlπ0=a0cos0+b0sin0=a0=∫02lcoslπ0coslπ0dx∫02lf(x)coslπ0dx=∫02lcos0cos0dx∫02lf(x)cos0dx=2l1∫02lf(x)dx
另外两个系数:
a n = ∫ 0 2 l f ( x ) c o s π l n x d x ∫ 0 2 l c o s π l n x c o s π l n x d x = 1 l ∫ 0 2 l f ( x ) c o s π l n x d x , n ∈ N a_n=\frac{\int_0^{2l}f(x)cos\frac{π}{l}nx\,dx}{\int_0^{2l}cos\frac{π}{l}nx\,cos\frac{π}{l}nx\,dx}=\frac{1}{l}\int_0^{2l}f(x)cos\frac{π}{l}nx\,dx,n\in N an=∫02lcoslπnxcoslπnxdx∫02lf(x)coslπnxdx=l1∫02lf(x)coslπnxdx,n∈N
b n = ∫ 0 2 l f ( x ) s i n π l n x d x ∫ 0 2 l s i n π l n x s i n π l n x d x = 1 l ∫ 0 2 l f ( x ) s i n π l n x d x , n ∈ N b_n=\frac{\int_0^{2l}f(x)sin\frac{π}{l}nx\,dx}{\int_0^{2l}sin\frac{π}{l}nx\,sin\frac{π}{l}nx\,dx}=\frac{1}{l}\int_0^{2l}f(x)sin\frac{π}{l}nx\,dx,n\in N bn=∫02lsinlπnxsinlπnxdx∫02lf(x)sinlπnxdx=l1∫02lf(x)sinlπnxdx,n∈N
三、借助欧拉公式进一步化简(另一组基)
令 π l = w \frac{π}{l}=w lπ=w,区间还是在 [ 0 , 2 l ] [0,2l] [0,2l] :
f ( x ) = a 0 + ∑ n = 1 + ∞ ( a n c o s ( n w x ) + b n s i n ( n w x ) ) (1) f(x)=a_0+\sum_{n=1}^{+∞}(a_n\,cos(nwx)+b_n\,sin(nwx))\tag{1} f(x)=a0+n=1∑+∞(ancos(nwx)+bnsin(nwx))(1)
欧拉公式:
e i θ = c o s θ + i s i n θ e − i θ = c o s θ − i s i n θ e^{i\theta}=cos\theta+i\,sin\theta\\ e^{-i\theta}=cos\theta-i\,sin\theta eiθ=cosθ+isinθe−iθ=cosθ−isinθ
即:
e i n w x = c o s ( n w x ) + i s i n ( n w x ) e − i n w x = c o s ( n w x ) − i s i n ( n w x ) e^{inwx}=cos(nwx)+i\,sin(nwx)\\ e^{-inwx}=cos(nwx)-i\,sin(nwx) einwx=cos(nwx)+isin(nwx)e−inwx=cos(nwx)−isin(nwx)
于是:
c o s ( n w x ) = e i n w x + e − i n w x 2 s i n ( n w x ) = e i n w x − e − i n w x 2 i cos(nwx)=\frac{e^{inwx}+e^{-inwx}}{2}\\ sin(nwx)=\frac{e^{inwx}-e^{-inwx}}{2i} cos(nwx)=2einwx+e−inwxsin(nwx)=2ieinwx−e−inwx
将上面两式代入式(1),得:
f ( x ) = a 0 + ∑ n = 1 + ∞ ( a n e i n w x + e − i n w x 2 + b n e i n w x − e − i n w x 2 i ) f(x)=a_0+\sum_{n=1}^{+∞}(a_n\,\frac{e^{inwx}+e^{-inwx}}{2}+b_n\,\frac{e^{inwx}-e^{-inwx}}{2i}) f(x)=a0+n=1∑+∞(an2einwx+e−inwx+bn2ieinwx−e−inwx)
下面开始化简:
f ( x ) = a 0 + ∑ n = 1 + ∞ ( a n e i n w x + e − i n w x 2 + i b n e i n w x − e − i n w x 2 i 2 ) f(x)=a_0+\sum_{n=1}^{+∞}(a_n\,\frac{e^{inwx}+e^{-inwx}}{2}+ib_n\,\frac{e^{inwx}-e^{-inwx}}{2i^2}) f(x)=a0+n=1∑+∞(an2einwx+e−inwx+ibn2i2einwx−e−inwx)
由于 i 2 = − 1 i^2=-1 i2=−1:
f ( x ) = a 0 + ∑ n = 1 + ∞ ( a n e i n w x + e − i n w x 2 − i b n e i n w x − e − i n w x 2 ) f(x)=a_0+\sum_{n=1}^{+∞}(a_n\,\frac{e^{inwx}+e^{-inwx}}{2}-ib_n\,\frac{e^{inwx}-e^{-inwx}}{2}) f(x)=a0+n=1∑+∞(an2einwx+e−inwx−ibn2einwx−e−inwx)
f ( x ) = a 0 + ∑ n = 1 + ∞ ( a n e i n w x − i b n e i n w x 2 + a n e − i n w x + i b n e − i n w x 2 ) f(x)=a_0+\sum_{n=1}^{+∞}(\frac{a_ne^{inwx}-ib_ne^{inwx}}{2}+\frac{a_ne^{-inwx}+ib_ne^{-inwx}}{2}) f(x)=a0+n=1∑+∞(2aneinwx−ibneinwx+2ane−inwx+ibne−inwx)
f ( x ) = a 0 + ∑ n = 1 + ∞ ( a n − i b n 2 e i n w x + a n + i b n 2 e − i n w x ) (2) f(x)=a_0+\sum_{n=1}^{+∞}(\frac{a_n-ib_n}{2}e^{inwx}+\frac{a_n+ib_n}{2}e^{-inwx})\tag{2} f(x)=a0+n=1∑+∞(2an−ibneinwx+2an+ibne−inwx)(2)
由于:
a n = 1 l ∫ 0 2 l f ( x ) c o s ( n w x ) d x b n = 1 l ∫ 0 2 l f ( x ) s i n ( n w x ) d x a_n=\frac{1}{l}\int_0^{2l}f(x)cos(nwx)\,dx\\ b_n=\frac{1}{l}\int_0^{2l}f(x)sin(nwx)\,dx an=l1∫02lf(x)cos(nwx)dxbn=l1∫02lf(x)sin(nwx)dx
a − n = 1 l ∫ 0 2 l f ( x ) c o s ( − n w x ) d x = a n a_{-n}=\frac{1}{l}\int_0^{2l}f(x)cos(-nwx)\,dx\\ =a_n a−n=l1∫02lf(x)cos(−nwx)dx=an
b − n = 1 l ∫ 0 2 l f ( x ) s i n ( − n w x ) d x = − b n b_{-n}=\frac{1}{l}\int_0^{2l}f(x)sin(-nwx)\,dx\\ =-b_n b−n=l1∫02lf(x)sin(−nwx)dx=−bn
于是式(2)可以整合:
f ( x ) = a 0 + ∑ n = 1 + ∞ ( a n − i b n 2 e i n w x + a n + i b n 2 e − i n w x ) f(x)=a_0+\sum_{n=1}^{+∞}(\frac{a_n-ib_n}{2}e^{inwx}+\frac{a_n+ib_n}{2}e^{-inwx}) f(x)=a0+n=1∑+∞(2an−ibneinwx+2an+ibne−inwx)
f ( x ) = a 0 + ∑ n = 1 + ∞ a n − i b n 2 e i n w x + ∑ n = 1 + ∞ a − n − i b − n 2 e − i n w x f(x)=a_0+\sum_{n=1}^{+∞}\frac{a_n-ib_n}{2}e^{inwx}+\sum_{n=1}^{+∞}\frac{a_{-n}-ib_{-n}}{2}e^{-inwx} f(x)=a0+n=1∑+∞2an−ibneinwx+n=1∑+∞2a−n−ib−ne−inwx
f ( x ) = a 0 + ∑ n = 1 + ∞ a n − i b n 2 e i n w x + ∑ n = − ∞ − 1 a n − i b n 2 e i n w x f(x)=a_0+\sum_{n=1}^{+∞}\frac{a_n-ib_n}{2}e^{inwx}+\sum_{n=-∞}^{-1}\frac{a_{n}-ib_{n}}{2}e^{inwx} f(x)=a0+n=1∑+∞2an−ibneinwx+n=−∞∑−12an−ibneinwx
f ( x ) = ∑ n = 0 0 a n e i n w x + ∑ n = 1 + ∞ a n − i b n 2 e i n w x + ∑ n = − ∞ − 1 a n − i b n 2 e i n w x f(x)=\sum_{n=0}^{0}a_ne^{inwx}+\sum_{n=1}^{+∞}\frac{a_n-ib_n}{2}e^{inwx}+\sum_{n=-∞}^{-1}\frac{a_{n}-ib_{n}}{2}e^{inwx} f(x)=n=0∑0aneinwx+n=1∑+∞2an−ibneinwx+n=−∞∑−12an−ibneinwx
最终整合成一个累加符号:
f ( x ) = ∑ n = − ∞ + ∞ c n e i n w x (3) f(x)=\sum_{n=-∞}^{+∞}c_ne^{inwx}\tag{3} f(x)=n=−∞∑+∞cneinwx(3)
当 n = 0 n=0 n=0 时,
c n = a 0 c_n=a_0 cn=a0
当 n ≠ 0 n≠0 n=0 时,
c n = a n − i b n 2 c_n=\frac{a_n-ib_n}{2} cn=2an−ibn
= 1 l ∫ 0 2 l f ( x ) c o s ( n w x ) d x − i 1 l ∫ 0 2 l f ( x ) s i n ( n w x ) d x 2 =\frac{\frac{1}{l}\int_0^{2l}f(x)cos(nwx)\,dx-i\frac{1}{l}\int_0^{2l}f(x)sin(nwx)\,dx}{2} =2l1∫02lf(x)cos(nwx)dx−il1∫02lf(x)sin(nwx)dx
= 1 l ∫ 0 2 l f ( x ) c o s ( n w x ) d x − 1 l ∫ 0 2 l f ( x ) i s i n ( n w x ) d x 2 =\frac{\frac{1}{l}\int_0^{2l}f(x)cos(nwx)\,dx-\frac{1}{l}\int_0^{2l}f(x)\,i\,sin(nwx)\,dx}{2} =2l1∫02lf(x)cos(nwx)dx−l1∫02lf(x)isin(nwx)dx
= 1 2 l ∫ 0 2 l f ( x ) [ c o s ( n w x ) − i s i n ( n w x ) ] d x =\frac{1}{2l}\int_0^{2l}f(x)[cos(nwx)-i\,sin(nwx)]dx =2l1∫02lf(x)[cos(nwx)−isin(nwx)]dx
= 1 2 l ∫ 0 2 l f ( x ) e − i n w x d x =\frac{1}{2l}\int_0^{2l}f(x)\,e^{-inwx}dx =2l1∫02lf(x)e−inwxdx
f ( x ) = ∑ n = − ∞ + ∞ c n e i n w x (3) f(x)=\sum_{n=-∞}^{+∞}c_ne^{inwx}\tag{3} f(x)=n=−∞∑+∞cneinwx(3)
式(3)意味着 f ( x ) f(x) f(x) 还能由另一组基的线性组合表示,该组基是复指数函数的集合:
{ . . . , e − i 2 w x , e − i w x , e 0 , e i w x , e i 2 w x , . . . } \{ {...\,,e^{-i2wx}\,,e^{-iwx}\,,e^{0}\,,e^{iwx}\,,e^{i2wx}\,,...\}} { ...,e−i2wx,e−iwx,e0,eiwx,ei2wx,...}
{ e i n w x ∣ n ∈ Z } \{ {e^{inwx}\,|\,n\in Z\}} { einwx∣n∈Z}
总结一下,傅里叶级数最终可以写成另一组基 { e i n w x ∣ n ∈ Z } \{ {e^{inwx}\,|\,n\in Z\}} { einwx∣n∈Z} 的线性组合:
f ( x ) = ∑ n = − ∞ + ∞ c n e i n w x f(x)=\sum_{n=-∞}^{+∞}c_ne^{inwx} f(x)=n=−∞∑+∞cneinwx
其中, c n c_n cn 是复数,
当 n = 0 n=0 n=0 时, c n = a 0 c_n=a_0 cn=a0
当 n ≠ 0 n≠0 n=0 时, c n = a n − i b n 2 = 1 2 l ∫ 0 2 l f ( x ) e − i n w x d x c_n=\frac{a_n-ib_n}{2}=\frac{1}{2l}\int_0^{2l}f(x)\,e^{-inwx}dx cn=2an−ibn=2l1∫02lf(x)e−inwxdx
参考:
1.傅里叶变换推导详解
https://zhuanlan.zhihu.com/p/77345128
2.傅里叶级数与傅里叶变换
https://zhuanlan.zhihu.com/p/366974965
3.我理解的傅里叶变换
https://zhuanlan.zhihu.com/p/23739221
4.如果看了这篇文章你还不懂傅里叶变换,那就过来掐死我吧
https://zhuanlan.zhihu.com/p/19759362
边栏推荐
- Verilog 状态机
- Detailed explanation of ThreadLocal
- GSE104154_scRNA-seq_fibrotic MC_bleomycin/normalized AM3
- Gradle notes
- Comment élaborer une stratégie nuageuse à l'ère des nuages mixtes
- 《MATLAB 神经网络43个案例分析》:第42章 并行运算与神经网络——基于CPU/GPU的并行神经网络运算
- /silicosis/geo/GSE184854_ scRNA-seq_ mouse_ lung_ ccr2/GSE184854_ RAW/GSM5598265_ matrix_ inflection_ demult
- ThreadLocal详解
- 表单自定义校验规则
- Docker安装canal、mysql进行简单测试与实现redis和mysql缓存一致性
猜你喜欢
随机推荐
Kotlin基础学习 14
Verilog state machine
KL divergence is a valuable article
Global and Chinese market of bone adhesives 2022-2028: Research Report on technology, participants, trends, market size and share
verilog REG 寄存器、向量、整数、实数、时间寄存器
Kubernetes cluster storageclass persistent storage resource core concept and use
Global and Chinese markets for electronic laryngoscope systems 2022-2028: Research Report on technology, participants, trends, market size and share
PY3, PIP appears when installing the library, warning: ignoring invalid distribution -ip
aaaaaaaaaaaaa
Kotlin 基础学习13
UI (New ui:: MainWindow) troubleshooting
Grpc快速实践
Verilog 过程连续赋值
Introduction to Robotics II. Forward kinematics, MDH method
JIT deep analysis
Discrimination between sap Hana, s/4hana and SAP BTP
Unity脚本的基础语法(8)-协同程序与销毁方法
Review materials of project management PMP high frequency examination sites (8-1)
Merge interval, linked list, array
Kotlin basic learning 17





![[HCIA continuous update] working principle of OSPF Protocol](/img/bc/4eeb091c511fd563fb1e00c8c8881a.jpg)