Three representations of signed numbers: original code, inverse code and complement code

One 、 Binary numbers in computers represent

（ One ） The representation of numbers

1、 Fixed-point number

• Fixed point numbers include fixed-point integers and fixed-point decimals
• Disadvantages of using fixed-point numbers
  ① When programming, you need to determine the decimal point position
  ② It is difficult to represent two numbers with large differences in size
  ③ Low utilization of storage space

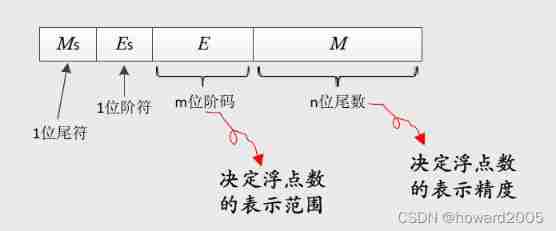
2、 Floating point numbers

（1） Floating point number concept

• The position of the decimal point can be moved left and right

（2） Normalize floating-point numbers

• The mantissa is expressed in pure decimal , That is... To the right of the decimal point 1 Not for 0
  

（ Two ） The nature of numbers

1、 An unsigned number

• All of the numbers 0 and 1 It's the data itself
• Various codes are mostly regarded as unsigned numbers

2、 Signed number

• need 0 or 1 Represent the properties of numbers （ Integers ）
• Numerical values are mostly regarded as signed numbers

3、 The nature of number is decided by the designer

• In low-level language programming , According to the nature of the number, it is processed by the program language （ Treat as unsigned or signed ）.

Two 、 An unsigned number

（ One ） Addition of unsigned numbers

• 0 + 0 = 0,0 + 1 = 1 ,1 + 0 = 1, 1 + 1 = 0（ Have carry ）

（ Two ） Subtraction of unsigned numbers

• 0 - 0 = 0,0 - 1 = 1（ There is an excuse ） 1 - 0 = 1,1 - 1 = 0

（ 3、 ... and ） Multiplication of unsigned numbers

• 0 × 0 = 0　0 × 1 = 0,1 × 0 = 0,1 × 1 = 1

（ Four ） The division of unsigned numbers

• 0 ÷ 0 = 0,0 ÷ 1 = 0,1 ÷ 0 = 0 （ meaningless ）,1 ÷ 1 = 1

（ 5、 ... and ） Multiplication and division case demonstration

• Multiplication ：00001011 × 0100 = 00101100B
• division ：00001011 ÷ 0100 = 00000010B
  – merchant = 00000010B
  – remainder = 11B
• Every times 2, Move left relative to the multiplicand 1 position
• Every time you divide by 2, Move right relative to the dividend 1 position

3、 ... and 、 Signed number

（ One ） Concept

• Use the highest bit to represent the symbol , The rest are values
• 0： It means a positive number
• 1： A negative number

（ Two ） Representation

1、 Original code

（1） Concept

• The highest bit is the sign bit , The rest is the truth part
• $[X{]}_{primary}=operatorNumberposition+|mostYesvalue|$

（2） advantage

• The correspondence between truth value and its original code representation is simple , Easy to understand

（3） shortcoming

• It is difficult to add and subtract with the original code in the computer
• 0 It's not unique

（4） Count 0 The original code of

8 digit 0 The original code of ：

• $+0=00000000$
• $-0=10000000$

thus it can be seen , Count 0 The original code is not unique .

2、 Inverse code

（1） Concept

Count a machine X：

• if $X>0$ , be $[X{]}_{back}=[X{]}_{primary}$
• if $X<0$, be $[X{]}_{back}=YesShould\; beprimarycodeOfoperatorNumberpositionNochange,CountvalueMinistrybranchPresspositionseekback$

（2） Case study

example 1、-52 The inverse of

$X=-52=-0110100$

• $[X{]}_{primary}=10110100$
• $[X{]}_{back}=11001011$

example 2、0 The inverse of

• $[+0{]}_{back}=[+0{]}_{primary}=00000000$
• $[-0{]}_{primary}=10000000$
• $[-0{]}_{back}=11111111$

thus it can be seen , Count 0 The inverse code of is not the only .

3、 Complement code

（1） Concept

For the number of machines X：

• $ifX>0,be[X{]}_{repair}=[X{]}_{back}=[X{]}_{primary}$
• $ifX<0,be[X{]}_{repair}=[X{]}_{back}+1$

（2） Case study

example 1、-52 Complement

$X=–52=–0110100$

• $[X{]}_{primary}=10110100$
• $[X{]}_{back}=11001011$
• $[X{]}_{repair}=[X{]}_{back}+1=11001100$

example 2、0 Complement

• $[+0{]}_{repair}=[+0{]}_{primary}=00000000$
• $[-0]repair=[-0{]}_{back}+1=11111111+1=100000000=00000000$
• explain ： Yes 8 The word is long , carry （ Red 1） Be abandoned

example 3、 Clock case - Move the pointer from 5 Dial to 1 spot

Dial two clocks ：

• Reverse the clock ：$5-4=1$
• Dial clockwise ：$5+8=13=12+1=1$ （$12$ For the mould , Automatically lost ）

To mold 12, Subtraction to addition

• $[-4{]}_{repair}=12-4=8$ （$8$ by $-4$ The complement of ）
• $5-4=5+8$
• $5-4=5+(-4)=5+(12-4)=5+8=12+1=1$

（3） Arithmetic operation of complement

By introducing complement , You can convert subtraction to addition .

• $[X+Y{]}_{repair}=[X{]}_{repair}+[Y{]}_{repair}$
• $[X-Y{]}_{repair}=[X+(-Y){]}_{repair}=[X{]}_{repair}+[-Y{]}_{repair}$

example 1、 Calculation 66-51

$66-51=66+(-51)=15$
Operate with binary complement ：

• $[+66{]}_{repair}=[+66{]}_{primary}=01000010$
• $[-51{]}_{primary}=10110011$
• $[-51{]}_{repair}=11001101$
• $[66-51{]}_{repair}=[+66]repair+[-51]repair=100001111=00001111=15$

example 2、X = -52 = -0110100,Y = 116 = +1110100, seek X + Y Value

• $[X{]}_{primary}=10110100$
• $[X{]}_{repair}=[X{]}_{back}+1=11001100$
• $[Y{]}_{repair}=[Y{]}_{primary}=01110100$
• $[X+Y{]}_{repair}=[X{]}_{repair}+[Y{]}_{repair}=11001100+01110100=01000000$
• The highest position is 0, The description is positive , The complement is equal to the original code , The sign bit + Truth value

$\therefore X+Y=[X+Y{]}_{repair}=01000000=+1000000=64$

example 3、X = 34 = +0100010,Y = -52 = -0110100, seek X + Y Value

• $[X{]}_{repair}=[X{]}_{primary}=00100010$
• $[Y{]}_{primary}=10110100$
• $[Y{]}_{repair}=[Y{]}_{back}+1=11001011+1=11001100$
• $[X+Y{]}_{repair}=[X{]}_{repair}+[Y{]}_{repair}=00100010+11001100=11101110$
• The highest position is 1, The explanation is negative , The complement is not equal to the original , Complement is not a sign bit + Truth value

$\therefore X+Y=[[X+Y{]}_{repair}{]}_{repair}=[11101110{]}_{repair}=[11101110{]}_{back}+1=10010001+1=10010010=-18$

（4） The compiler system converts negative numbers into complements

• In modern computer systems , When programming , Negative numbers can be used “-” Express , The compiler converts it into complement .
• Case presentation ： If input number $=-3$, The compiled value of the program $=FDH$
• $X=-3=-0000011$
• $[X{]}_{primary}=10000011$
• $[X{]}_{repair}=[X{]}_{back}+1=11111100+1=11111101=FDH$

（5） Special number 10000000

• To an unsigned number ：$(10000000{)}_B=128$
• In the original code, it is defined as ：$(10000000{)}_B=-0$
• It is defined as ：$(10000000{)}_B=-127$
• Defined in the complement as ：$(10000000{)}_B=-128$

Four 、 Limitations of computer capabilities

（ One ） The computing power of a computer is limited

• Computers can't solve the problem that they can't design algorithms
• Unable to handle infinite operations or continuously changing information

（ Two ） The number that a computer can represent （ Table number ） The scope of is limited

• The range of computer tables is limited by word length

• Yes 8 For bit machines
  – The maximum number of unsigned numbers ：$11111111$
  – The maximum value of a signed positive number ：$01111111$

• When the operation result exceeds the range of computer tables , There will be an overflow

1、 The representation range of unsigned integers

• When the running result of the number in the computer exceeds the range of the number of tables , Then there is overflow .
• Table number range of unsigned integers ： $0\le X\le 2^n-1$（$n$ Indicates word length ）
• Judgment method of unsigned number addition and subtraction overflow ： When there is a carry from the highest to the higher （ Or borrow a seat ） Overflow occurs when .
  

2、 The representation range of signed integers

（1） Original code and inverse code

• $-(2^{n-1}-1)\le X\le 2^{n-1}-1$

（2） Complement code

• $-2^{n-1}\le X\le 2^{n-1}-1$

（3） Yes 8 Bit binary number

• Original code ： $-127～+127$
• Inverse code ： -$127～+127$
• Complement code ： $-128～+127$

（4） Overflow judgment in symbolic number operation

• When two signed binary numbers are added or subtracted , If the result of the operation is beyond the expressible range , Then there is overflow

• Judgment method of overflow ： Carry state of the highest bit $⨁$ Secondary high carry status ＝1, The result overflows .

• example ： If the carry state of the highest bit is different from that of the second highest bit, it will overflow
  

• When the division operation overflows , produce " Divisor is 0" interrupt

• There is no overflow problem in multiplication

5、 ... and 、 Symbol binary number and decimal conversion

（ One ） Transformation method

1. Find the true value
2. convert

（ Two ） The number of symbols in the computer is expressed in the form of complement by default

• Original code = Sign bit + The absolute value
• A complement to a positive number = Original code = Sign bit + The absolute value
• A negative complement ≠ Original code $*$ A negative complement ≠ Sign bit + The absolute value

（ 3、 ... and ） The complement number is converted to decimal number

1、 Positive number

• Complement code = Inverse code = Original code , And the original code = Sign bit + Truth value $*$ The numeric part of the positive complement is the true value

2、 For negative numbers

• Complement code ≠ Inverse code ≠ Original code $*$ The numeric part of the negative complement ≠ Truth value

3、 Case presentation

（1） The highest complement is 0 The situation of

• hypothesis $[X{]}_{repair}=00101110_B$
  The sign bit is 0, The description is positive , Complement code = Original code = Sign bit + Truth value
  therefore , Truth value $=+0101110_B*X=+101110_B=+46$

（2） The highest complement is 1 The situation of

• hypothesis $[X{]}_{repair}=11010010_B$
• The sign bit is 1, The explanation is negative ,$X\ne -1010010_B$
• desire $X$ Truth value , Need for $[X{]}_{repair}$ Make up again
• $X=[[X{]}_{repair}{]}_{repair}=[11010010_B{]}_{repair}=[11010010_B{]}_{back}+1=10101101_B+1=10101110_B=-0101110_B=-46$