Basic concepts of tree

Summary

        This chapter first introduces the relevant theoretical knowledge of binary tree , Then give C Detailed implementation of the language . Learning about binary trees , It should be noted that ： It's not hard , Not only is it not difficult , And it's very simple . When I first came into contact with trees , I also think it seems very difficult ; This feeling is mainly due to a lot of strange concepts of binary trees 、 Nature and other contents . And when I really realized the binary tree and looked back at its related concepts and properties , I think it is so simple ！ therefore , When learning binary tree ： First, the basic concept of binary tree 、 Have a basic understanding of nature , Encounter difficult knowledge points , You can draw pictures to help understand ; After having a basic concept , And then I will personally implement the binary search tree ( This is crucial !); Finally, when I come back to summarize the theoretical knowledge of binary trees , You'll find that —— It's really simple ！ In code practice , I take " Binary search tree , Not just a binary tree " Explain for example , A simple binary tree is very simple , It's rarely used in practice . Besides, I have mastered the binary search tree , The binary tree will be mastered naturally .

      The binary search tree implemented in this article is C Language version of the , In the following chapters C++ and Java Implementation of version . You can practice learning according to your familiar language ！

      Please understand deeply 、 Practice and master " Binary search tree "！ It is the later study AVL Trees 、 Stretch the tree 、 The cornerstone of red black tree and other related tree structures ！

Catalog
1.  Introduction to the tree
2.  Introduction to binary tree
3.  Binary search tree C Realization
4.  Binary search tree C The test program

Reprint please indicate the source ： Binary search tree ( One ) And Graphic analysis and C The realization of language - If the sky doesn't die - Blog Garden

---

More :  Data structure and algorithm series Catalog  

(01).  Binary search tree ( One ) And Graphic analysis and C The realization of language
(02).  Binary search tree ( Two ) And C++ The implementation of the
(03).  Binary search tree ( 3、 ... and ) And Java The implementation of the

Introduction to the tree

1. The definition of a tree

A tree is a data structure , It is from n（n>=0） Finite nodes make up a set with hierarchical relationships .

• If n=0, It's called the empty tree
• If n>0, be ：
  • There is a specific called root （root） The node of , It has only direct successors , But there is no direct precursor
  • Nodes other than the root are divided into m(m>=0) A finite set of disjoint T0,T1,...,Tn-1, Each set is a tree , And call it the subtree of the root （subtree）

Call it "it". “ Trees ” Because it looks like an upside down tree , That is to say, it is root up , And leaf down . It has the following characteristics ：
(01) Each node has zero or more children ;
(02) A node without a parent is called a root node ;
(03) Each non root node has and only has one parent node ;
(04) Except for the root node , Each sub node can be divided into several disjoint sub trees .

2. The basic term for trees

If a node has a subtree , Then the node is called the root of the subtree " Parents ", The root of the subtree is the root of the node " children ". Nodes with the same parents are each other " brother ". Any node on all subtrees of a node is the descendant of that node . All nodes on the path from the root node to a node are the ancestors of the node .

The degree of node ： The number of subtrees owned by the node .
leaf ： A node of degree zero .
Branching nodes ： Nodes with degree not zero .
The degree of a tree ： The maximum degree of a node in a tree .

level ： The level of the root node is 1, The hierarchy of the other nodes is equal to the hierarchy of the parent nodes of the node plus 1.
The height of the tree ： The maximum level of nodes in a tree .
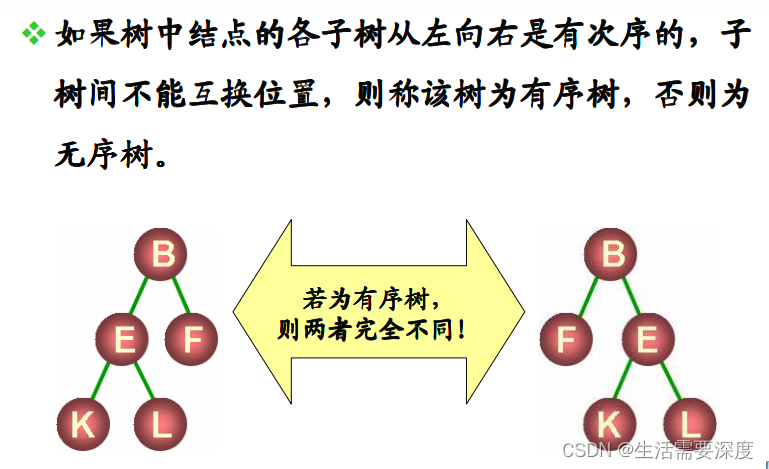
Disordered trees ： If the order between the subtrees of the nodes in the tree is not important , You can switch places .
Ordered trees ： If the order between the subtrees of nodes in a tree is important , You can't swap places .
The forest ：0 One or more disjoint trees make up . Add a root to the forest , The forest becomes a tree ; Delete the root , Trees become forests .

 

 

 

 

 1.3 Design common operations in the tree

2. The storage structure of the tree

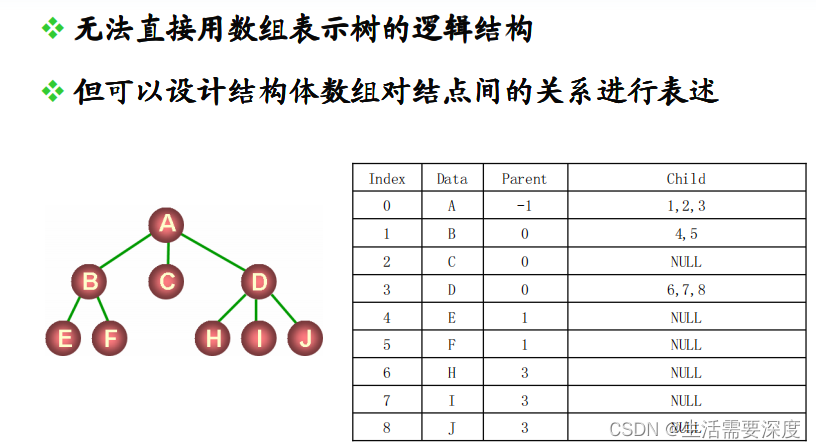
  The tree structure needs to add or delete nodes , Whether array storage can be flexible ？ Each node can have multiple child nodes , How to store ？

 2.2 The tree stores node relationships

The general tree representation method is based on the parent-child representation model , In this representation, each node has a pointer to its double clearing , Each node has several pointers to its children .

Another tree structure model is called the child brother representation model , Each node has a pointer to its first child , Each node has a pointer to its first right sibling .

Each node corresponding to this structure contains a data pointer and two node pointers ：

• The data pointer points to the data stored in the tree
• The child node pointer points to the first child
• The sibling node pointer points to the first right sibling  

 

 

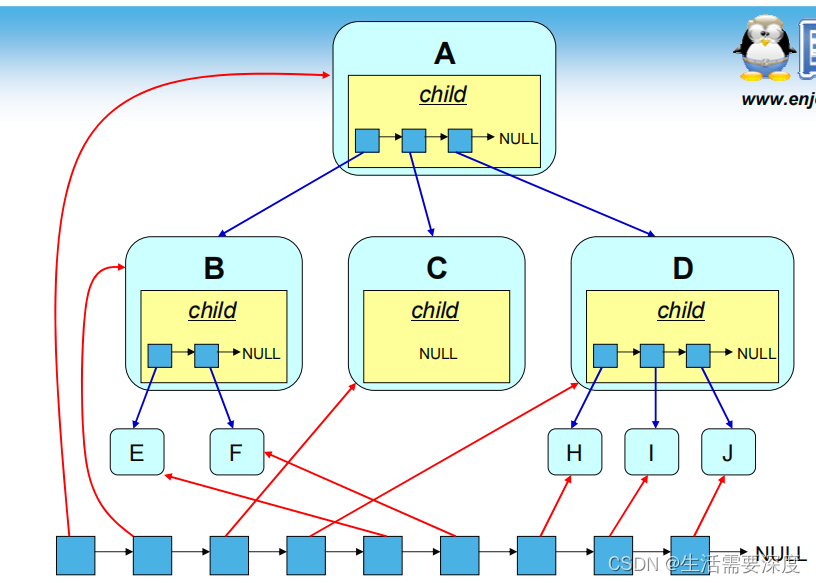
Characteristics of the representation of children's brothers ：

• Can represent any tree structure
• There are only three pointer fields in each node , Data pointer 、 Child node pointer 、 Sibling node pointer
• The structure of each node is simple , Only the child node pointer and brother node pointer constitute the tree branch  

Choose to use a linked list to organize tree nodes , Storage nodes that can be traversed , The maintenance of linked lists is complicated .