Quick completion guide of manipulator (10): accessible workspace

Directory ：

Quick completion guide of mechanical arm （ zero ）： Main contents and analysis methods of the guide

Quick completion guide of mechanical arm （ One ）： The development of manipulator

Quick completion guide of mechanical arm （ Two ）： Application of mechanical arm

Quick completion guide of mechanical arm （ 3、 ... and ）： Mechanical structure of mechanical arm

Quick completion guide of mechanical arm （ Four ）： Reducer of key components of mechanical arm

Quick completion guide of mechanical arm （ 5、 ... and ）： End actuators

Quick completion guide of mechanical arm （ 6、 ... and ）： Stepper motor driver

Quick completion guide of mechanical arm （ 7、 ... and ）： Description method of robot arm posture

Quick completion guide of mechanical arm （ 8、 ... and ）： Kinematic modeling （ standard DH Law ）

Quick completion guide of mechanical arm （ Nine ）： Forward kinematics analysis

Quick completion guide of mechanical arm （ Ten ）： Reachable workspace

******************** Here is the main body ********************

 

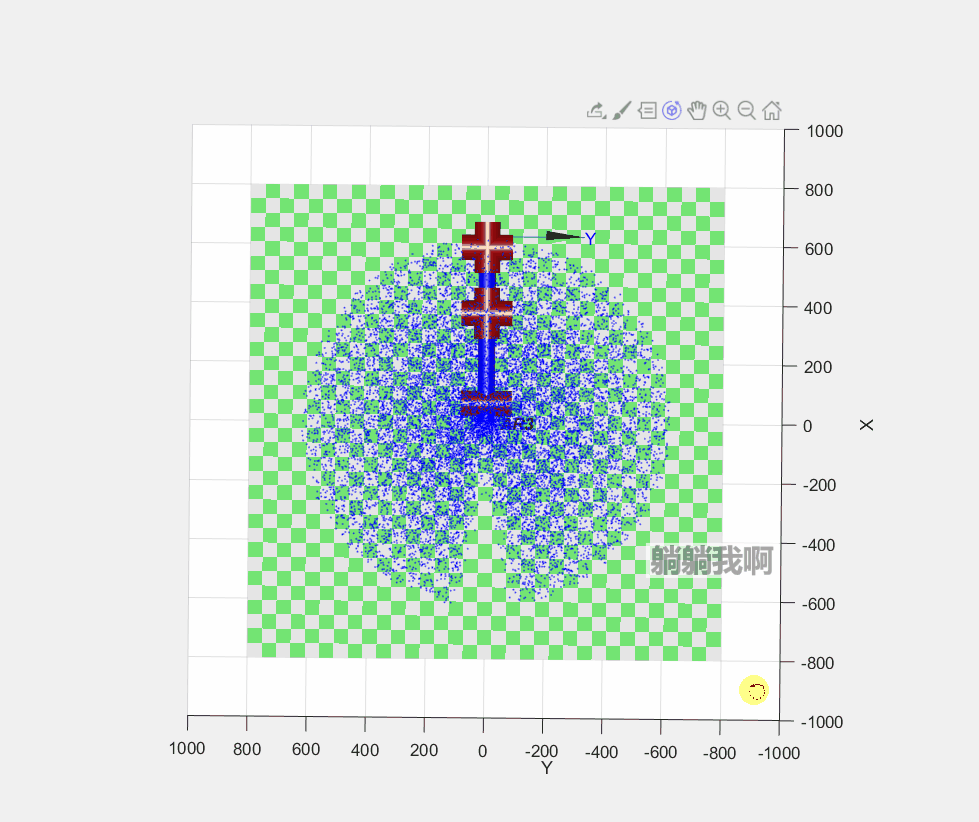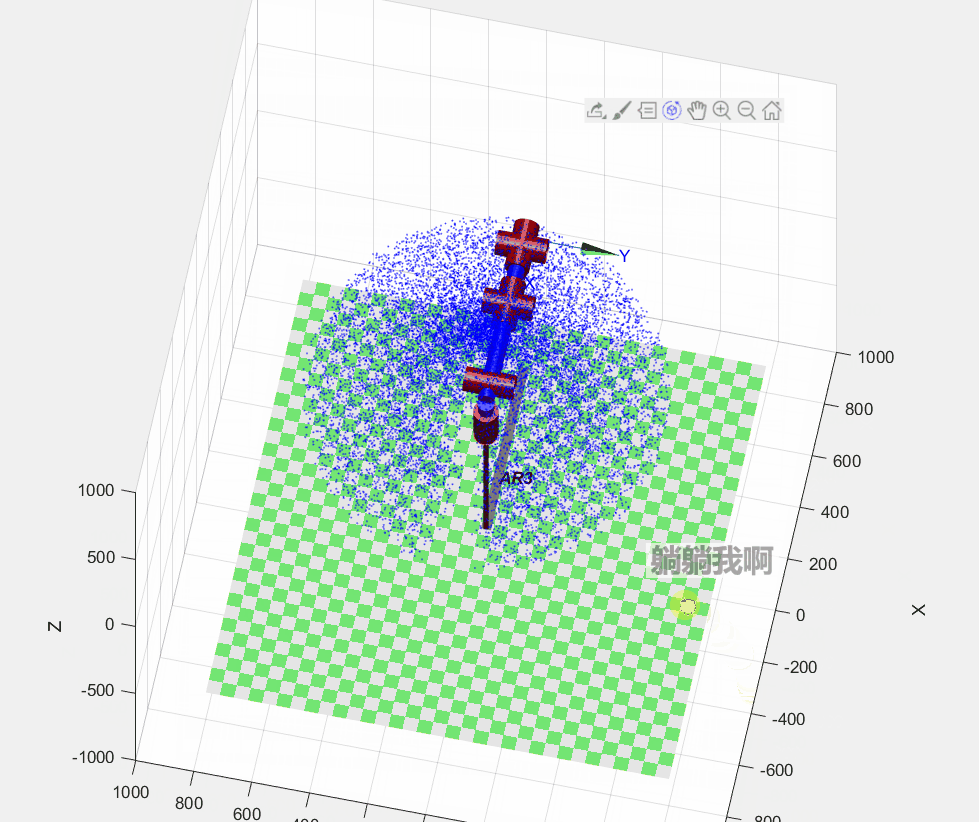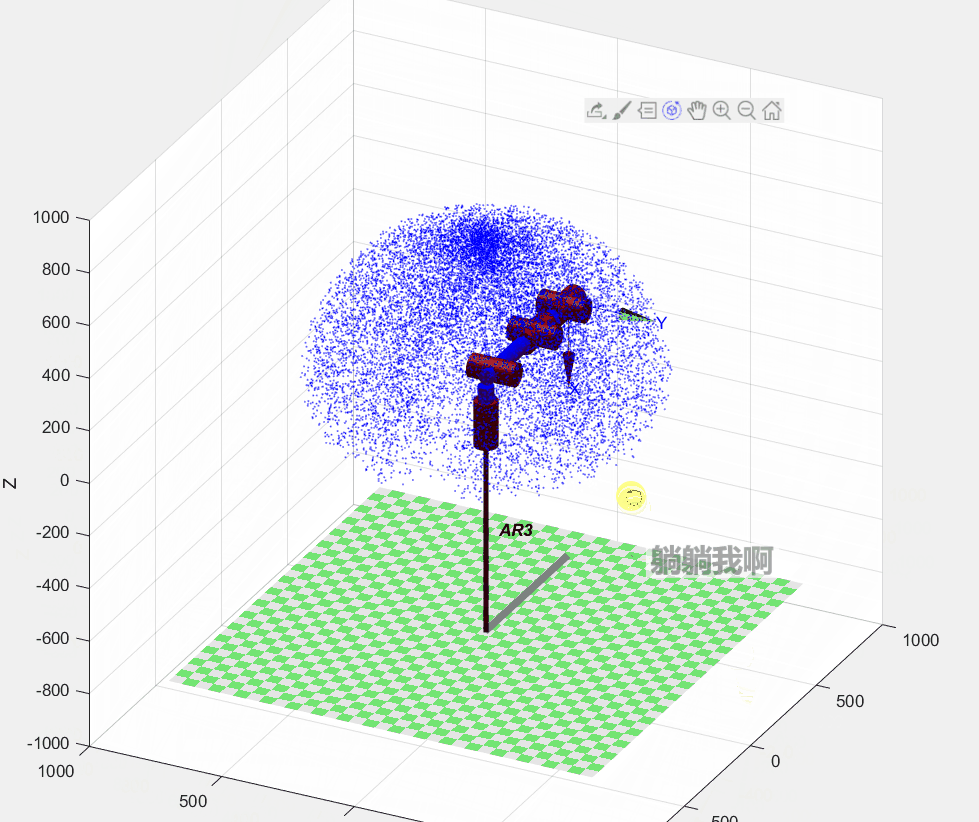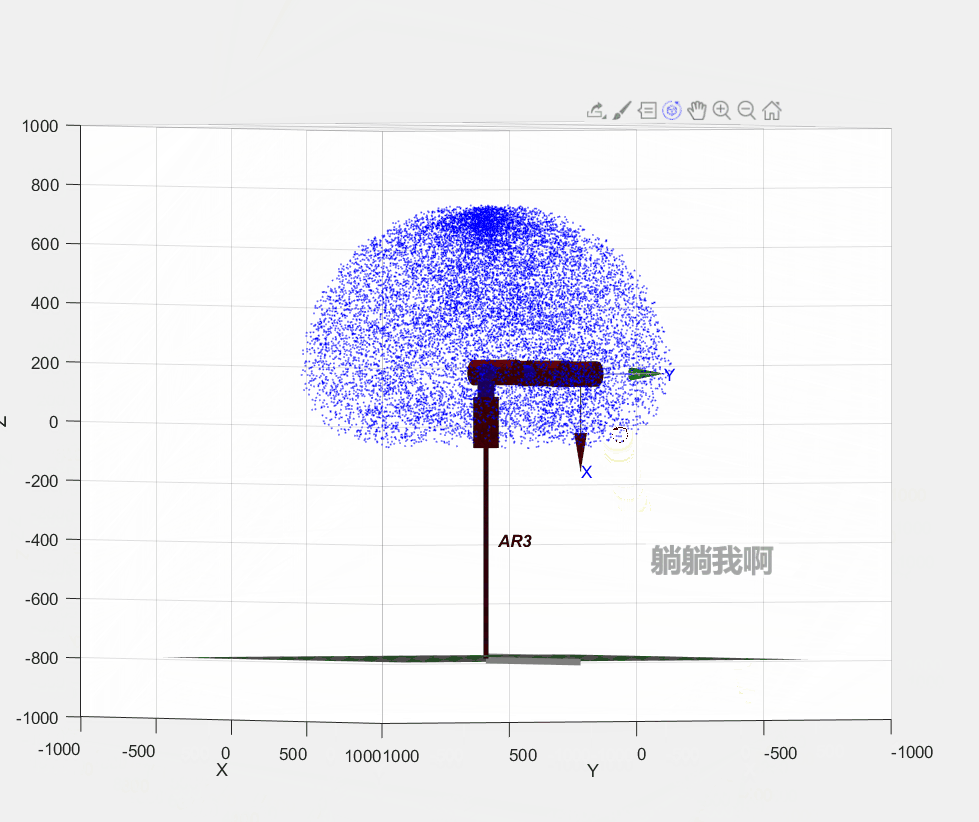
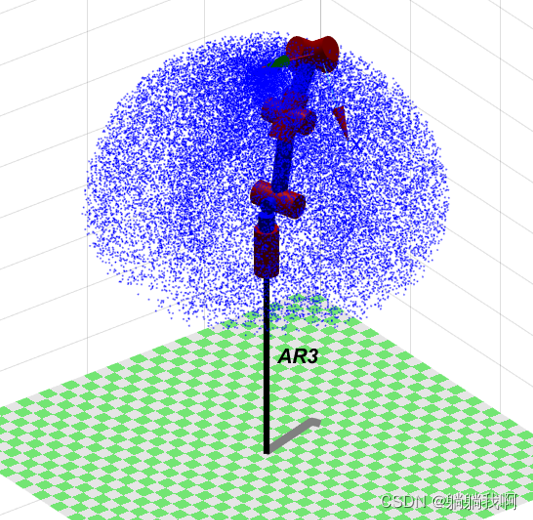
         stay guide （ Nine ） in , We have obtained a six degree of freedom manipulator Forward kinematics equation , By substituting joint variables into the equation, the position and posture of the end of the manipulator can be obtained . Now we know the rotatable range of each joint , that , At the same time, we can also get all the positions that the end of the manipulator can reach , We call this set of possible locations as Reachable workspace , And this is also an important parameter index of the manipulator .

         Used in the guide MATLAB Medium Robotic Toolbox hold-all （ It's not official Robotics System Toolbox ） Kinematic simulation of the manipulator , The reachable workspace of the manipulator is obtained by Monte Carlo method, which is easy to implement and runs fast .

One 、 Joint space and drive space

         Joint space description and driver space description are two methods used to describe the pose of manipulator .

1. Joint space

         For one with n For a manipulator with three degrees of freedom , The positions of all its connecting rods can be determined by a group n Joint variables are confirmed
set . Such a set of variables is often called nx1 Joint vector . The space composed of all joint vectors is called Joint space .

2. Drive space

         up to now , We have always assumed that every joint is directly driven by some kind of driver . However , This is not the case for many industrial robots , Sometimes we also use two drivers to drive a joint in a differential way , Sometimes, a linear driver is used to drive the rotating joint through a four-bar linkage .

         In these cases , You need to consider the drive space . Because the sensor that measures the joint change of the manipulator is usually installed on the driver , Therefore, in some calculations, the joint vector must be expressed as a set of driver functions , Drive vector . The space composed of all drive vectors is called Drive space .

Two 、 working space （workspace）

         working space (workspace) It is when all the joints of the manipulator perform all the possible movements , A collection of the origin positions of the end effector coordinate system . The workspace can be divided into Can be up to (reachable) working space And flexible (dexterous) working space .

        Workspace is Co., LTD. 、 closed 、 coherent Of . Because joints are rotating or moving , It is easy to know that the workspace is composed of a plane 、 spherical 、 Composed of surface elements such as ring and cylinder . Manipulator manufacturers will give the workspace of the manipulator in the form of top view and flat view in the data manual , It is the basic element needed to evaluate the performance of the robot in the expected application .

1. Reachable workspace

        The set of target points reached by the manipulator end effector in more than one direction is Reachable workspace .

2. Flexible workspace

         The set of target points that the manipulator can reach in any direction is Flexible workspace .

3. Programming realization of reachable workspace calculation of manipulator

% Monte Carlo method simulates the reachable workspace of the manipulator 
% Liu lie 
radian1 = pi/180;

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Definition DH Parameters %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Liu lie %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
d1 = 169.77;
d2 = 0;
d3 = 0;
d4 = -222.63;
d5 = 0;
d6 = -36.25;

% Mechanical arm link length parameter a
a1 = 64.2;
a2 = 305;
a3 = 0;
a4 = 0;
a5 = 0;
a6 = 0;

% Parameters of joint deflection angle of manipulator alpha
alpha1 = -90 * radian1;
alpha2 =   0 * radian1;
alpha3 =  90 * radian1;
alpha4 = -90 * radian1;
alpha5 =  90 * radian1;
alpha6 =   0 * radian1;

% Define joint angle limits 
lim1_min = -170 * radian1; lim1_max = 170 * radian1; % The joints 1(-170,170)
lim2_min = -132 * radian1; lim2_max =   0 * radian1; % The joints 2(-132,0)
lim3_min =    1 * radian1; lim3_max = 141 * radian1; % The joints 3(1,141)
lim4_min = -165 * radian1; lim4_max = 165 * radian1; % The joints 4(-165,165)
lim5_min = -105 * radian1; lim5_max = 105 * radian1; % The joints 5(-105,105)
lim6_min = -155 * radian1; lim6_max = 155 * radian1; % The joints 6(-155,155)

% Define the range of joint rotation 
lim1 = lim1_max - lim1_min;
lim2 = lim2_max - lim2_min;
lim3 = lim3_max - lim3_min;
lim4 = lim4_max - lim4_min;
lim5 = lim5_max - lim5_min;
lim6 = lim6_max - lim6_min;

%  Define each link and joint type , The default is to rotate the joint 
%           θ  d    a    α         Angle limit                          Joint offset 
L(1)=Link([ 0   d1   a1   alpha1]); L(1).qlim=[lim1_min,lim1_max];
L(2)=Link([ 0   d2   a2   alpha2]); L(2).qlim=[lim2_min,lim2_max];
L(3)=Link([ 0   d3   a3   alpha3]); L(3).qlim=[lim3_min,lim3_max];  L(3).offset=-pi/2;
L(4)=Link([ 0   d4   a4   alpha4]); L(4).qlim=[lim4_min,lim4_max];
L(5)=Link([ 0   d5   a5   alpha5]); L(5).qlim=[lim5_min,lim5_max];
L(6)=Link([ 0   d6   a6   alpha6]); L(6).qlim=[lim6_min,lim6_max];  L(6).offset=pi;

% Combine the above connecting rods 
AR3=SerialLink(L,'name','AR3');
% Displays the number of manipulator joints and D_H parameter list 
%AR3:: 6 axis, RRRRRR, stdDH, slowRNE
AR3.display();

% Use Monte Carlo method to draw the workspace of the manipulator 
N=15000;
theta1 = ( lim1_min + (lim1 * rand(N,1)) );
theta2 = ( lim2_min + (lim2 * rand(N,1)) );
theta3 = ( lim3_min + (lim3 * rand(N,1)) );
theta4 = ( lim4_min + (lim4 * rand(N,1)) );
theta5 = ( lim5_min + (lim5 * rand(N,1)) );
theta6 = ( lim6_min + (lim6 * rand(N,1)) );

for n = 1:N
    theta = [theta1(n),theta2(n),theta3(n),theta4(n),theta5(n),theta6(n)];
    workspace = AR3.fkine(theta);
    plot3(workspace.t(1),workspace.t(2),workspace.t(3),'b.','markersize',1);
    hold on;
end
AR3.plot(theta);  % Animation display 
% Real time display of robots 
AR3.teach();

         The specific programming process is ： First, according to the definition in the previous chapter Kinematic parameters of manipulator Yes Robotic Toolbox Assignment of relevant parameters of the manipulator in the toolbox , In order to build the simulation model of the manipulator ; next , Generate 30000 Random joint variables , Substitute Forward kinematics equation To solve the ; Last , Mark the points representing the reachable position of the end effector in three-dimensional space , The dot matrix formed can represent the Reachable workspace , The running effect of the program is shown in the figure below .