当前位置:网站首页>基于最小二乘法的线性回归分析方程中系数的估计
基于最小二乘法的线性回归分析方程中系数的估计
2022-08-02 14:10:00 【杨老头软工】
一、问题描述
一元线性回归分析时一种非常简单也是非常基本的回归理论,能够用来刻画两个变量之间的以线性关系的变化趋势,进而预测未知点处的数据。
回归分析就是根据已知数据的变化趋势来确定回归函数(方程),其中回归系数待定,而后利用一些数值方法或者统计方法来估计回归系数。
一元线性回归分析就是估计方程y=kx+b是中的系数k和b,常见的方法有:计算数学的方法——最小二乘法、统计方法——最大似然估计法、机器学习方法——感知机等,此外还可以利用矩阵的运算(其实是极小值解而已)来直接求解。
本文以y = 2x + 1和y=-2x+5的数据进行拟合为例,给出了利用最小二乘法来估计回归系数的方法及matlab实现。
二、数学推导
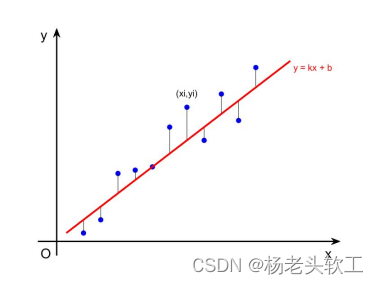
问题描述:
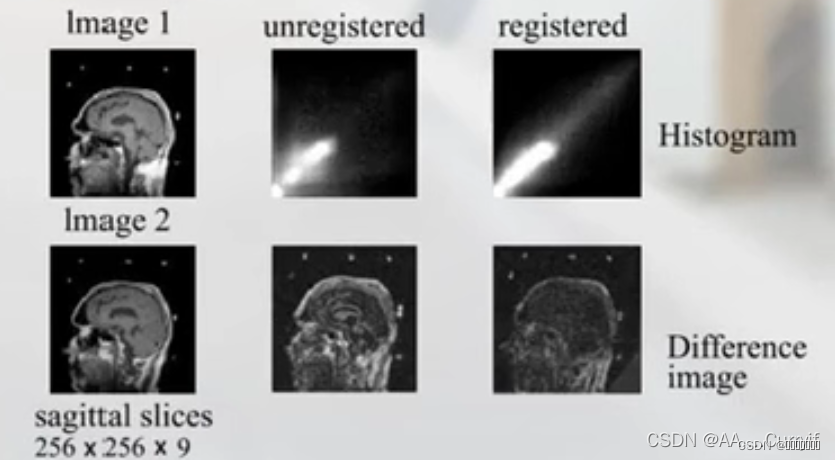
如上图所示,假设已知数据点(xi,yi),i=1…n,且经过散点图的观察基本满足线性变化趋势,据此求出红色直线的函数表达式。
如上图所示,最小二乘法就是利用途中黑色线段所表示已知点到回归曲线的距离平方和最小来估计回归函数中待定系数。
公式推导如下:
把(xi,yi)代入y=kx+b得:
构造最小二乘函数(距离平方和):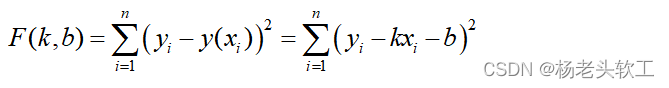
对k和b分别求偏导数得: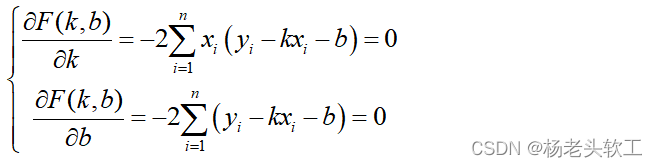
上述方程组两端同时除以数据点个数n得: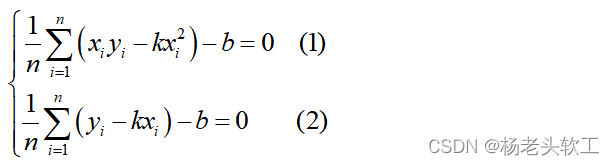
方程(2)可以进一步转化为:
其中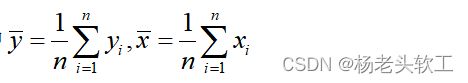
将
代入(1)得:

将k代入
即可得到系数b,至此,回归方程中的两个系数计算完毕。
三、Matlab程序
1.根据散点图判读曲线变化趋势
trainX = linspace( 0, 2, 50 );
trainY = 2 * trainX + 1 + randn( size( trainX ) )*0.4;
plot( trainX, trainY, 'b.', 'markersize', 20 )
如下图所示:
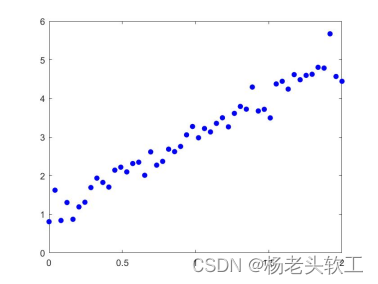
从图中点的分布情况可以看出基本呈现线性增长的趋势,因此可以考虑使用y=kx+b来拟合该组数据。
2.回归系数计算如下:
n = length( trainX );
xu = sum( trainX ) / n;
yu = sum( trainY ) / n;
k1 = sum( trainX .* trainY ) - n * xu * yu;
k2 = sum( trainX .* trainX ) - n * xu * xu;
k = k1 / k2;
b = yu - k * xu;
计算结果为:
K = 1.8467, b = 1.2669
3.完整的代码如下:
% 利用最小二乘法估计线性回归函数y = kx + b中的系数k和b
clear all
clc
%生成训练数据
trainX = linspace( 0, 2, 50 );
trainY = 2 * trainX + 1 + randn( size( trainX ) )*0.4;
%绘制散点图
plot( trainX, trainY, 'b.', 'markersize', 20 )
%估计回归系数
n = length( trainX );
xu = sum( trainX ) / n;
yu = sum( trainY ) / n;
k1 = sum( trainX .* trainY ) - n * xu * yu;
k2 = sum( trainX .* trainX ) - n * xu * xu;
k = k1 / k2;
b = yu - k * xu;
%绘制回归函数曲线(直线)
hold on
x = [ -0.5 ; 2.5 ];
y = k * x + b; %回归方程
plot( x, y, 'r', 'LineWidth', 2 );
title( 'LSM : y = 2x + 1' )
axis( [ -0.5, 2.5, -1, 7 ] )
拟合结果如下: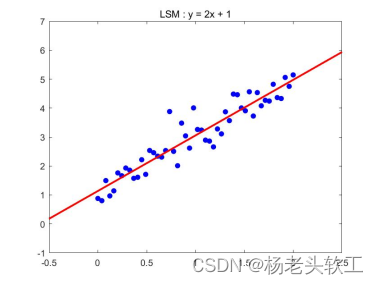
修改语句 “trainY = 2 * trainX + 1 + randn( size( trainX ) )*0.1;”
为不同的函数关系,即可得到不同回归曲线。例如修改为
“trainY = -2 * trainX -5 + randn( size( trainX ) )*0.4;”
可以得到如下拟合图像: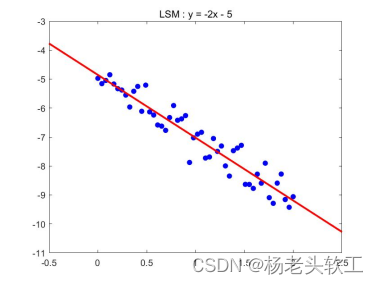
四、补充说明
最小二乘法是一种非常优秀的利用求函数极值来估计回归方程中参数的方法,事实上,极大似然法估计回归系数的目标函数虽然不一样,但是结果和直接利用最小二乘法估计的结果是一样。
边栏推荐
猜你喜欢
随机推荐
FP7195降压恒流PWM转模拟调光零压差大功率驱动方案原理图
Binder ServiceManager解析
“非图灵完备”到底意味着什么
将SSE指令转换为ARM NEON指令
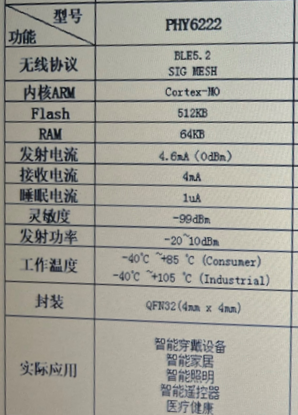
BLE蓝牙5.2-PHY6222系统级芯片(SoC)智能手表/手环
Letter combination of LeetCode2 phone number
What should I do if Windows 10 cannot connect to the printer?Solutions for not using the printer
How to add a one-key shutdown option to the right-click menu in Windows 11
2020-02-06-快速搭建个人博客
ASR6601牛羊定位器芯片GPS国内首颗支持LoRa的LPWAN SoC
SQL的通用语法和使用说明(图文)
使用npx -p @storybook/cli sb init安装失败,手把手搭建专属的storybook
pytorch模型转libtorch和onnx格式的通用代码
General syntax and usage instructions of SQL (picture and text)
让深度学习歇一会吧
基于51单片机和物联网的智能家居系统(ESP8266物联网模块)
Please make sure you have the correct access rights and the repository exists.问题解决
如何用硬币模拟1/3的概率,以及任意概率?
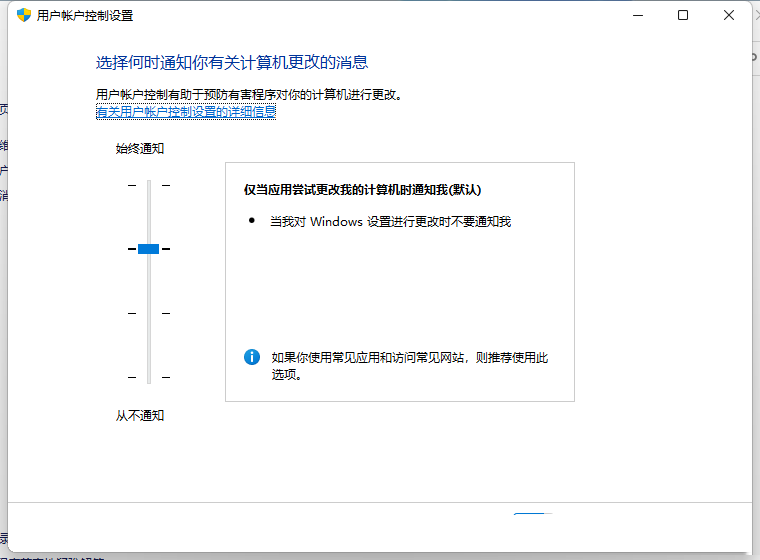
Win11 keeps popping up User Account Control how to fix it
Mapreduce环境详细搭建和案例实现