当前位置:网站首页>The linear table lookup
The linear table lookup
2022-08-05 02:46:00 【cute horse】
1、顺序查找
(1)顺序查找介绍
顺序查找的查找过程为:从表的一端开始,Sequentially compares the recorded key with the given value,If the key of a record is the same as the given value,则查找成功;反之,If after scanning the entire table,Still no records with the key equal to the given value were found,则查找失败!
Suitable for linear and linked lists!
(2)、代码实现
(1)、顺序查找
//顺序查找
int Search_Seq(SSTable S,int key){
for (int i = S.length - 1; i >= 1 ; i-- ) //i = S.length - 1,S.data[S.length - 1] = -1结束标志符
{
if (S.data[i] == key)
return i; //Search from front to back is successful!
}
return 0; //查找失败
}
But each step in the above algorithm checks to see if the entire table has been searched,That is, the loop variable must be judged every time the loop is looped i >= 1 的检测.The following search algorithm for sentinel monitoring is an improvement on this situation!
(2)、Sets the sequential lookup for sentry surveillance
Sequential lookups for sentinel monitoring will look for values key 放在S.data[0]中,然后执行操作!
//Sequential search for sentry surveillance
int Search_Seq1(SSTable S,int key){
//Find from back to front until i = 0,At this point, the search failed;否则会返回 1 ~ S.length - 1 number of positions in between
int i;
S.data[0] = key;
for ( i = S.length - 1; S.data[i] != key ; i-- );
return i;
}
When this algorithmS.length >= 1000的时候,The actual lookup is almost cut in half
(3)、所有代码如下
#include<string.h>
#include<stdio.h>
#define MaxSize 20
#include<iostream>
#include<stdlib.h>
#define endl '\n'
using namespace std;
typedef struct{
int *data;
int length;
}SSTable;
void InputElement(SSTable &S){
S.data = (int *) malloc (sizeof(int)*MaxSize);
S.length = 1;
cout<<"\n请输入要排序的数!结束请输入 -1 :";
for (int i = 1 ; i < MaxSize && S.data[i-1] != -1; i++){
//将S.data[0]闲置不用
cin>> S.data[i];
S.length++;
}
int i = 1;
cout<<"\n输入如下:";
while(S.data[i] != -1){
cout<<S.data[i]<<" ";
i ++;
}
}
//顺序查找
int Search_Seq(SSTable S,int key){
for (int i = S.length - 1; i >= 1 ; i-- ) //i = S.length - 1,S.data[S.length - 1] = -1结束标志符
{
if (S.data[i] == key)
return i; //Search from front to back is successful!
}
return 0; //查找失败
}
//Sequential search for sentry surveillance
int Search_Seq1(SSTable S,int key){
//Find from back to front until i = 0,At this point, the search failed;否则会返回 1 ~ S.length - 1 number of positions in between
int i;
S.data[0] = key;
for ( i = S.length - 1; S.data[i] != key ; i-- );
return i;
}
main(){
SSTable S;
InputElement(S);
cout<<"\n\n请输入查找关键字:";
int key;
cin>>key;
if (Search_Seq(S,key))
cout<<"\n查找成功!In the sequence table is the first "<<Search_Seq(S,key)<<" 个元素!\n";
else
cout<<"\n查找失败!\n";
cout<<"\n-----------------------------------------前后对比如下-----------------------------------------------------\n";
if (Search_Seq1(S,key))
cout<<"\n查找成功!In the sequence table is the first "<<Search_Seq1(S,key)<<" 个元素!\n";
else
cout<<"\n查找失败!\n";
}
(4)、结果测试
(3)、算法分析
The advantage of sequential search is that:算法简单,There are no requirements for table structure,既适用于顺序结构,At the same time, it is suitable for chain structure,Applies whether or not the records are sorted by key!But its average lookup lengthASL比较大,ASL = 1/n * (1 + 2 + 3 + …+ n) = (n + 1)/2,So its search efficiency is very low.When looking for the numbern很大的时候,Sequence tables are not suitable!
2、折半查找(二分查找)
(1)、二分查找介绍
The halved search is a more efficient search method,However, the halved search requires that the linear table must adopt a sequential storage structure,Because the sequential table has more characteristics than random access access,而链表没有,Therefore, binary search cannot be implemented using linked lists!And the elements in the table must be ordered,要么升序要么降序,If not it cannot be usedRealize the comparison and halving search(The following code implementation assumes ascending order)
从表的中间记录开始,If the value of the lookup is equal to the value of the intermediate record,则查找成功;If lookup value and key greater than or less than the middle record,则在表中大于或小于中间记录的那一半中查找,这样重复操作,直到查找成功!或者在某一步中查找区间为空,则代表查找失败!
(2)、代码实现
#include<string.h>
#include<stdio.h>
#define MaxSize 20
#include<iostream>
#include<stdlib.h>
#define endl '\n'
using namespace std;
typedef struct{
int *data;
int length;
}SSTable;
//输入数
void InputElement(SSTable &S){
S.data = (int *) malloc (sizeof(int)*MaxSize);
S.length = 1;
cout<<"\n请输入要排序的数!结束请输入 -1 :";
for (int i = 0 ; i < MaxSize && S.data[i-1] != -1; i++){
cin>> S.data[i];
S.length++;
}
int i = 0;
cout<<"\n输入如下:";
while(S.data[i] != -1){
cout<<S.data[i]<<" ";
i ++;
}
}
int Search_Bin(SSTable S,int key){
int low = 0, high = S.length -1,mid;
while(low <= high){
//查找成功的情况
mid = (low + high)/2;
if (S.data[mid] == key)
return mid;
else if(S.data[mid] > key)
high = mid - 1;
else
low = mid + 1;
}
return 0; //查找失败,即low > high
}
main(){
SSTable S;
InputElement(S);
cout<<"\n\n请输入查找关键字:";
int key;
cin>>key;
if (Search_Bin(S,key))
cout<<"\n查找成功!In the sequence table is the first "<<Search_Bin(S,key)+1<<" 个元素!\n";
else
cout<<"\n查找失败!\n";
}
当 low = high的时候,The last element of the search interval needs to be judged!
(3)、算法分析
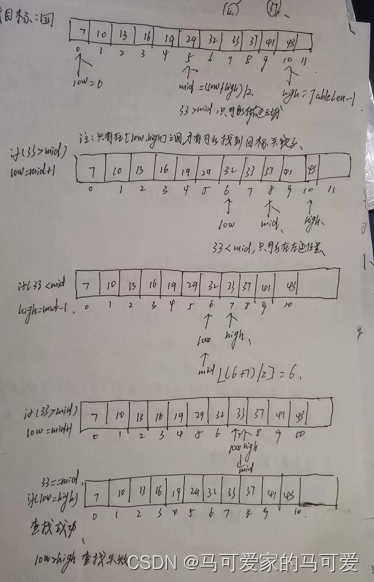
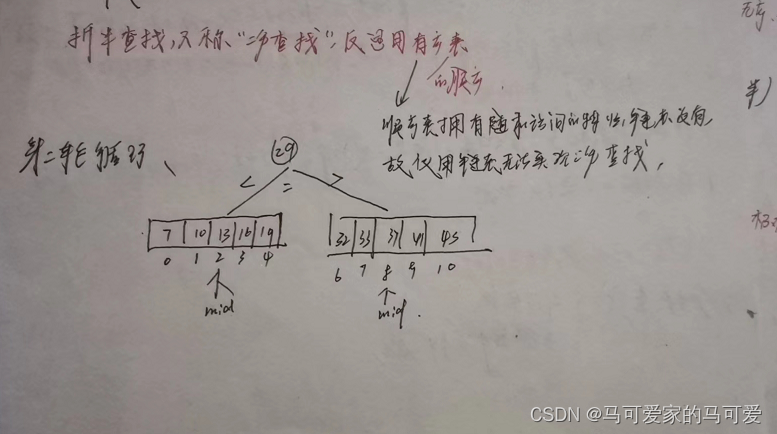
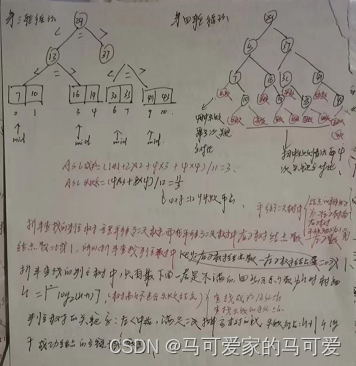
So the halved search can be described using a binary tree!由此可见,The number of keywords to be compared when the search is successful in the halved search must not exceed the depth of the tree!The shape of the decision tree is only related to the number of table records n 有关,It has nothing to do with the value of the keyword!We know in Chapter 5,具有nThe height of a binary tree of nodes is h = 【log 2 n】+ 1(向下取整);或h = 【log 2 (n+1)】向上取整.Therefore, when the search is successful, the number of keywords that are compared with the given value is at most no more than half 树高h!
The key for the decision tree:左 < 中 < 右,满足 二叉排序树 的定义,The failed node is n + 1个,is the successful nodeThe number of empty chain domains,Therefore, when the search fails, the number of keywords that are compared with the given value is at most more than 树高h!
So the time complexity of the halved search is O(log 2 n)!
折半查找的优点是:查找次数少,查找效率高,But it must be an ordered sequential list,而不是链表!并且,Must be sorted before searching!同时为了保持顺序表的有序性,When inserting or deleting a table,On average, half of the elements in the moving table are compared.因此,The halved lookup is not suitable for linear tables with frequently changing data elements!
(4)、平均查找长度
ASL = (n+1)/n * log2 (n + 1)- 1 当nWhen it is larger, it can be directly taken asASL = log2 (n + 1)- 1
3、分块查找(索引顺序查找)
(1)、分块查找介绍
It is a search method with performance between sequential search and halved search!
分块查找的基本思想:
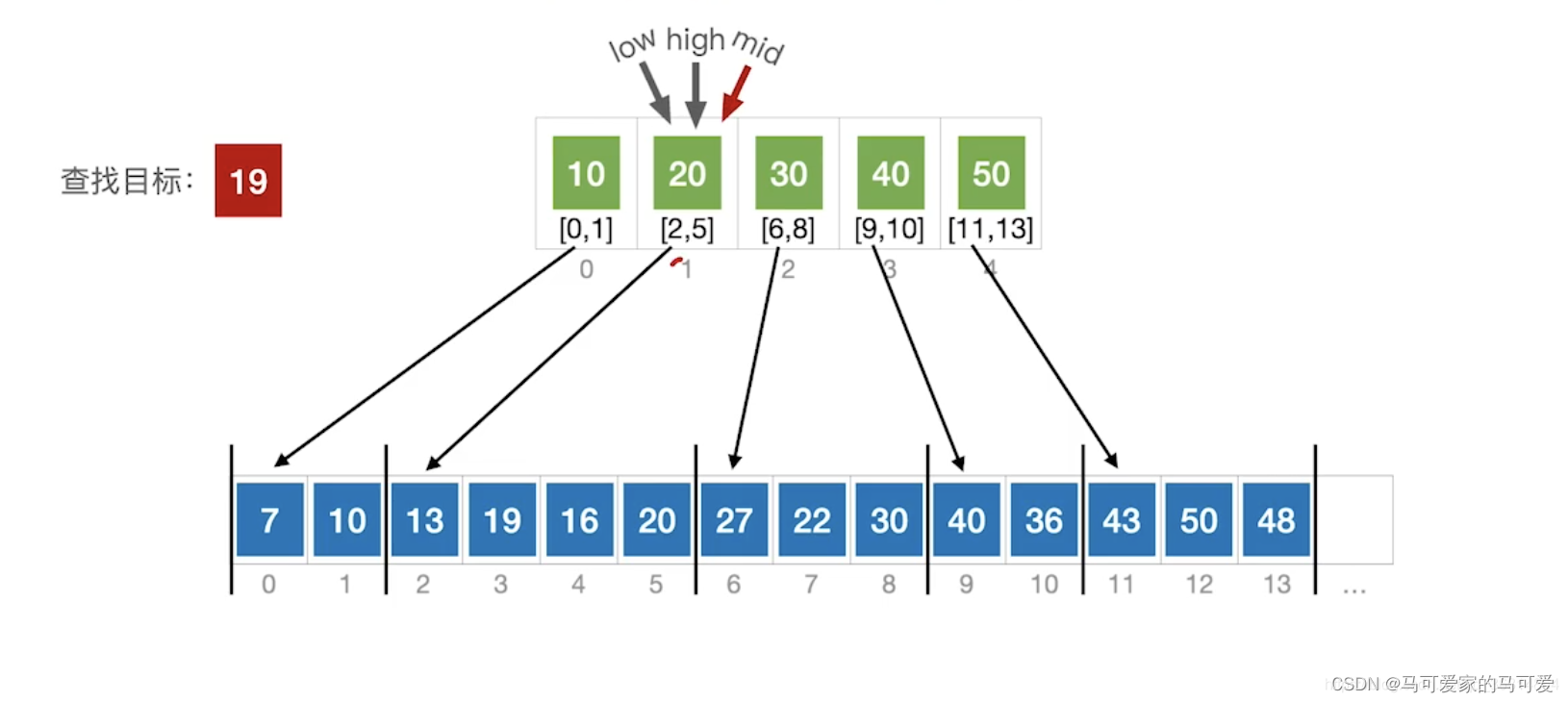
将查找表分为若干子块.块内的元素可以无序,但块之间是有序的,即第一个块中的最大关键字小于第二个块中的所有记录的关键字,第二个块中的最大关键字小于第三个块中的所有记录的关键字,以此类推.再建立一个索引表,索引表中的每个元素含有各块的最大关键字和各块中的第一个元素的地址,索引表按关键字有序排列(The kingly way is that each element contains the largest key of each block and the address of the first element and the address of the last element in each block)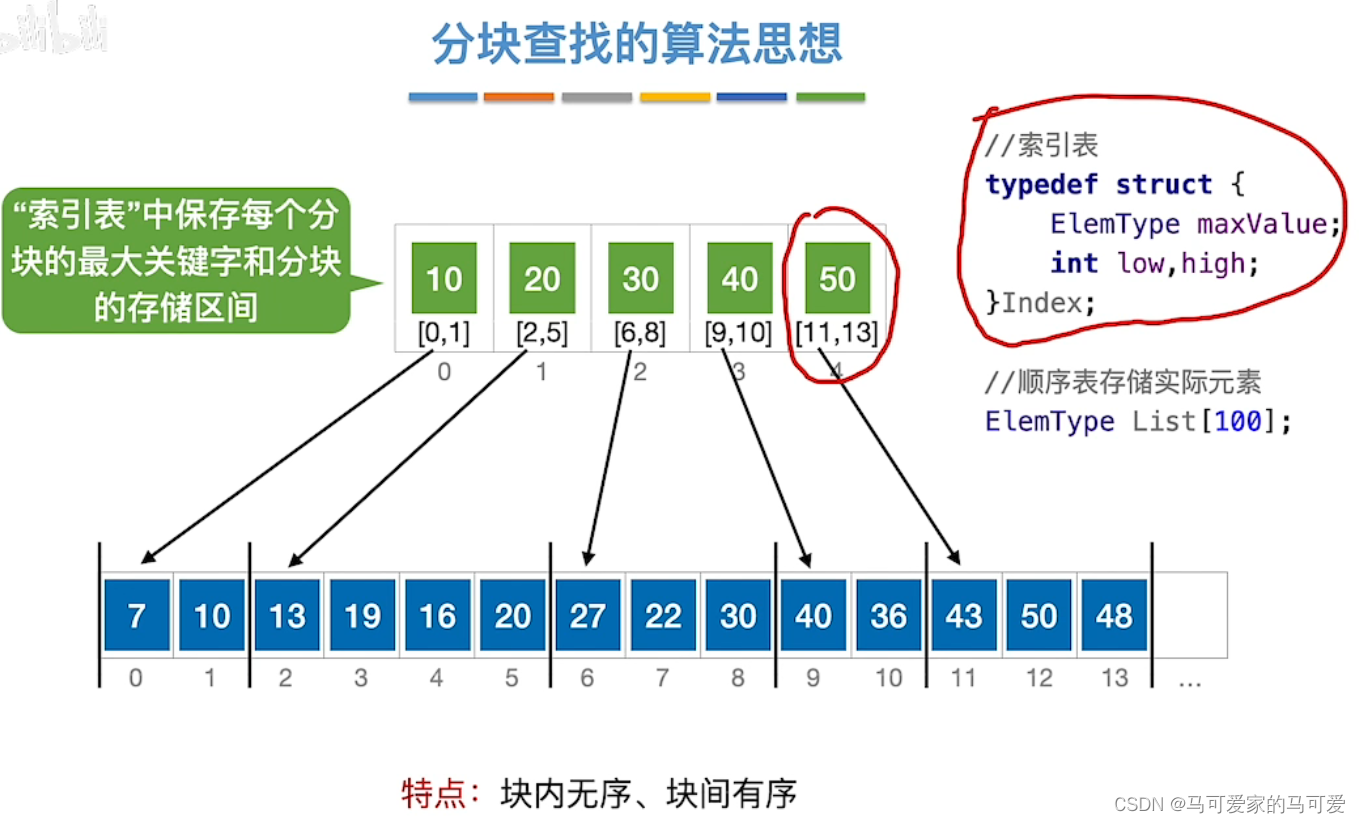
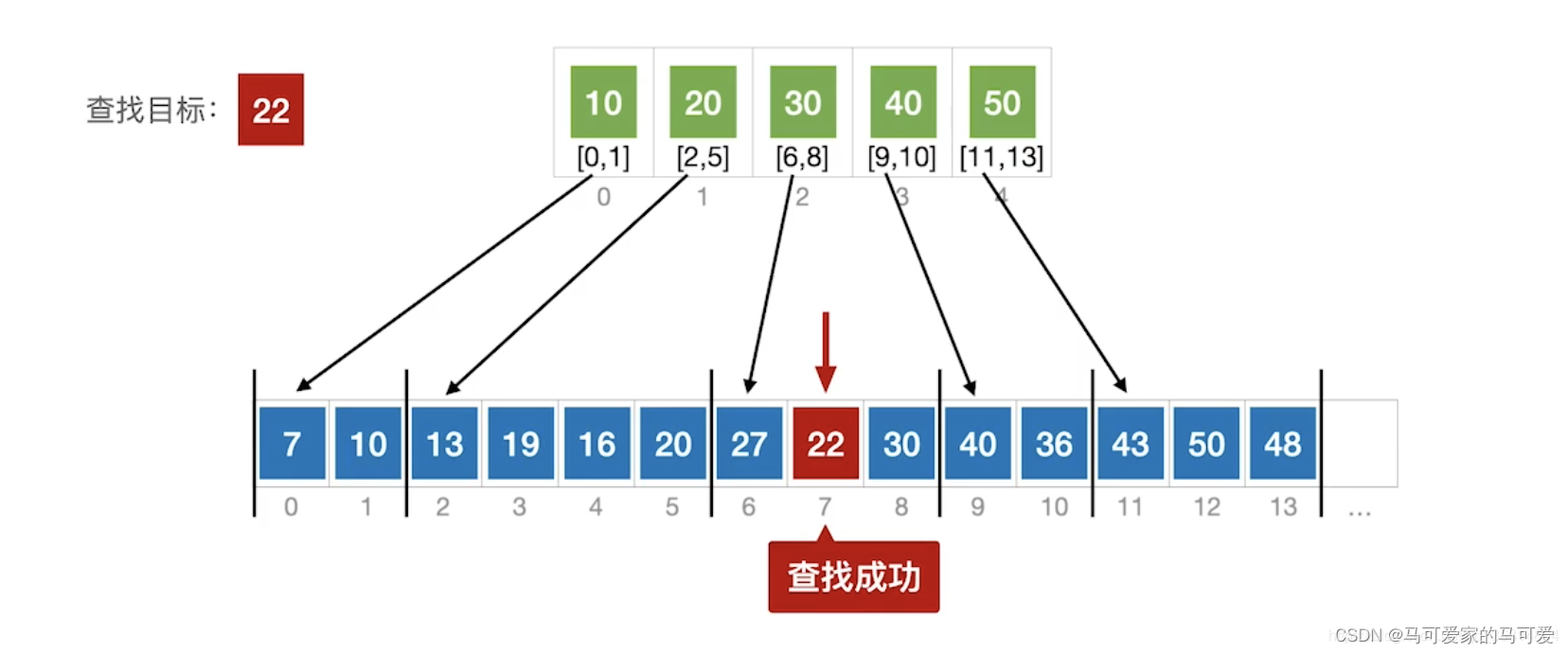
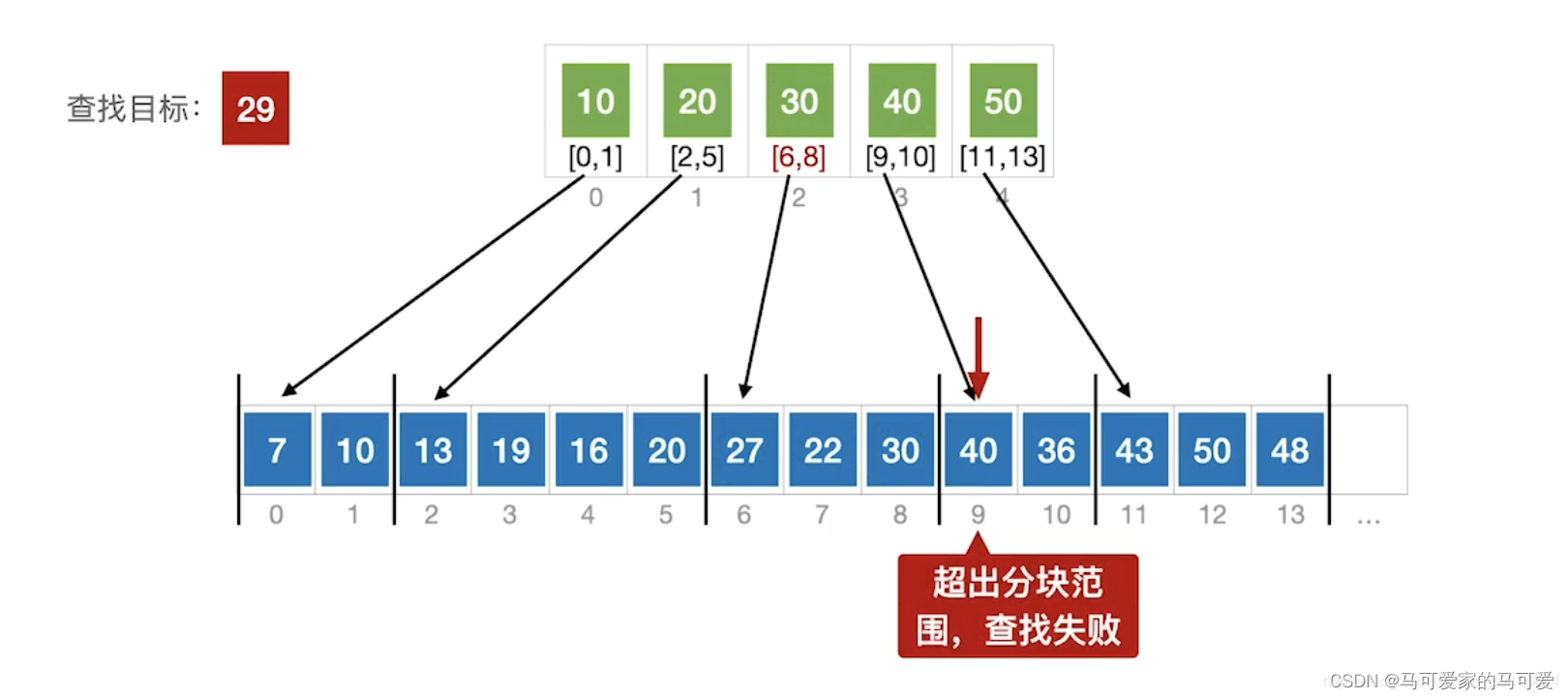
(2)、分块查找的过程
● 第一步是在索引表中确定待查记录所在的块,可以顺序查找或折半查找索引表.
● 第二步是在块内顺序查找.
(3)、Use the halved lookup index table
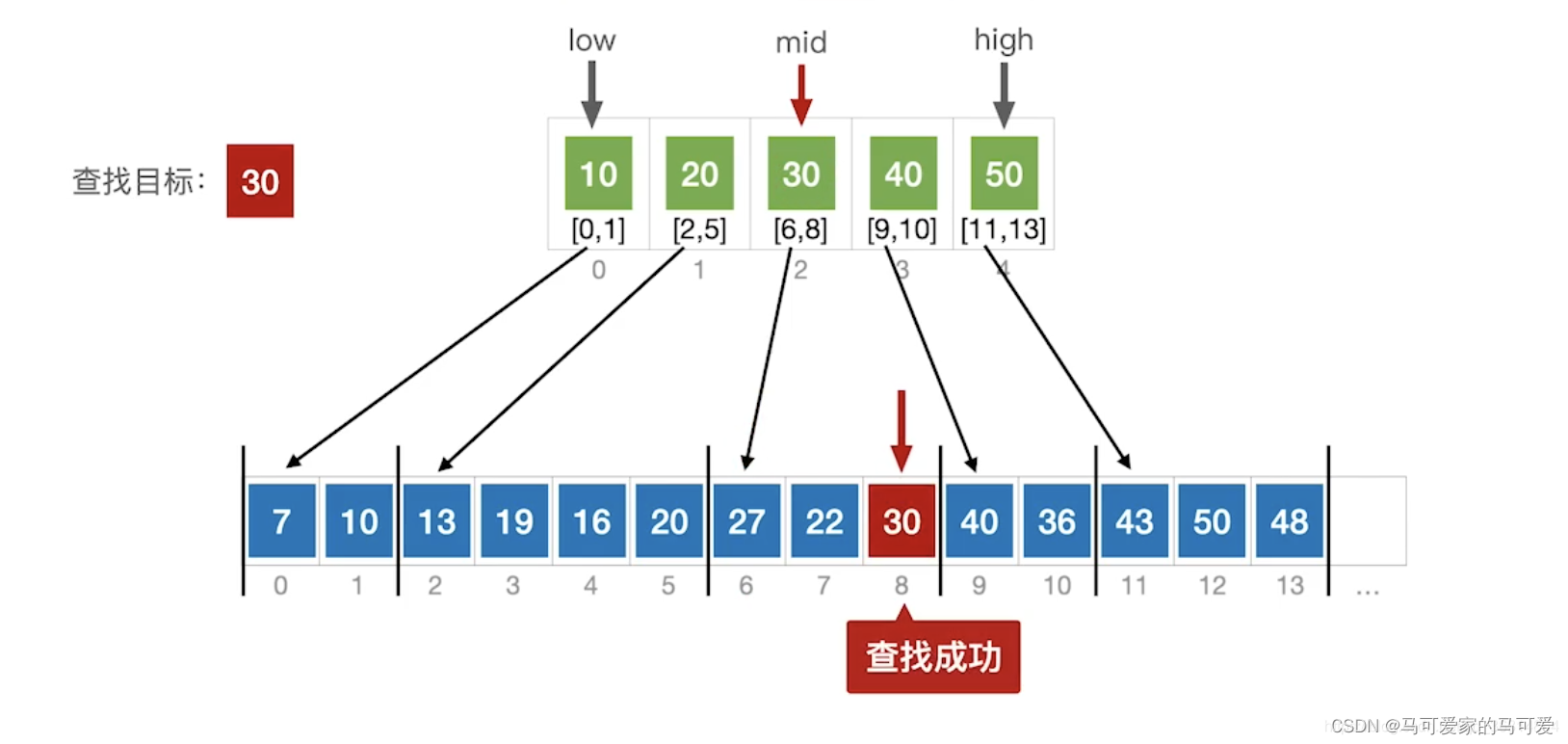
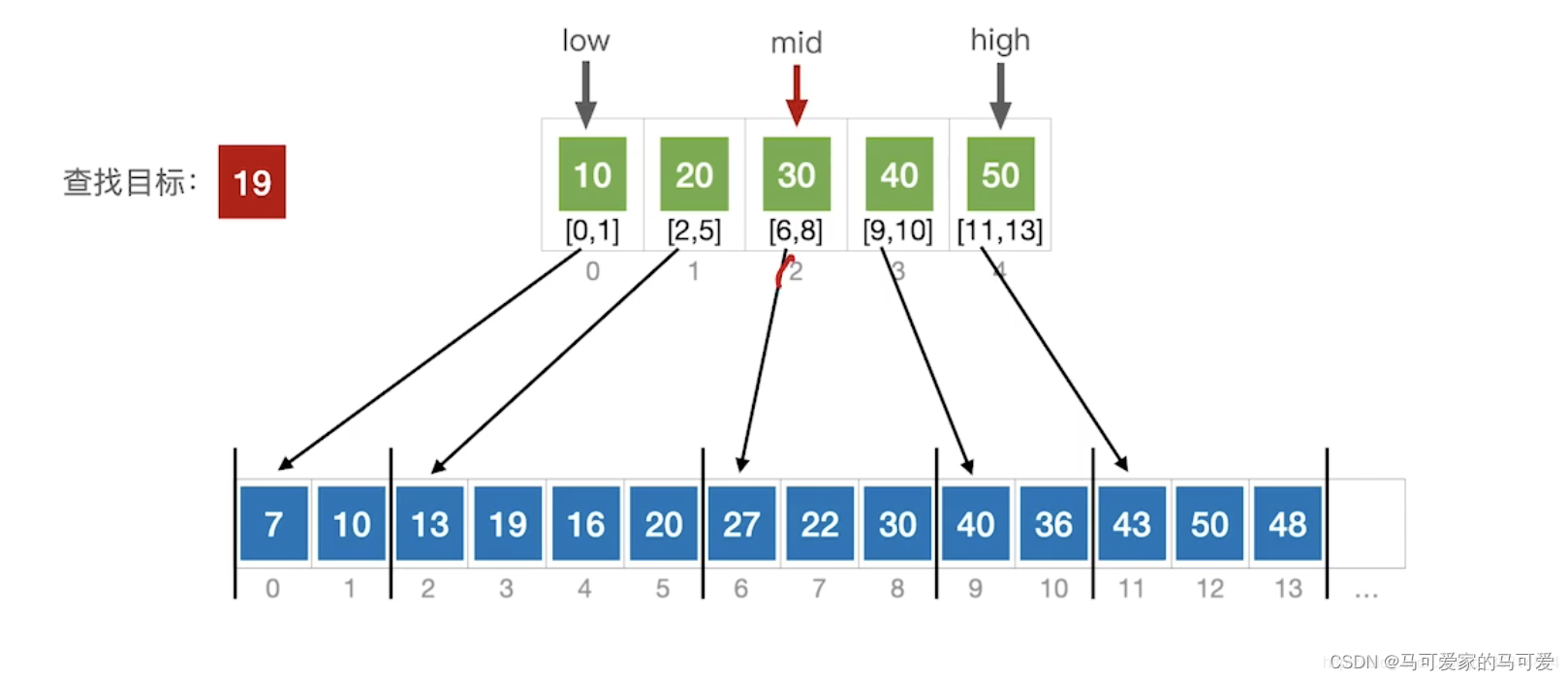
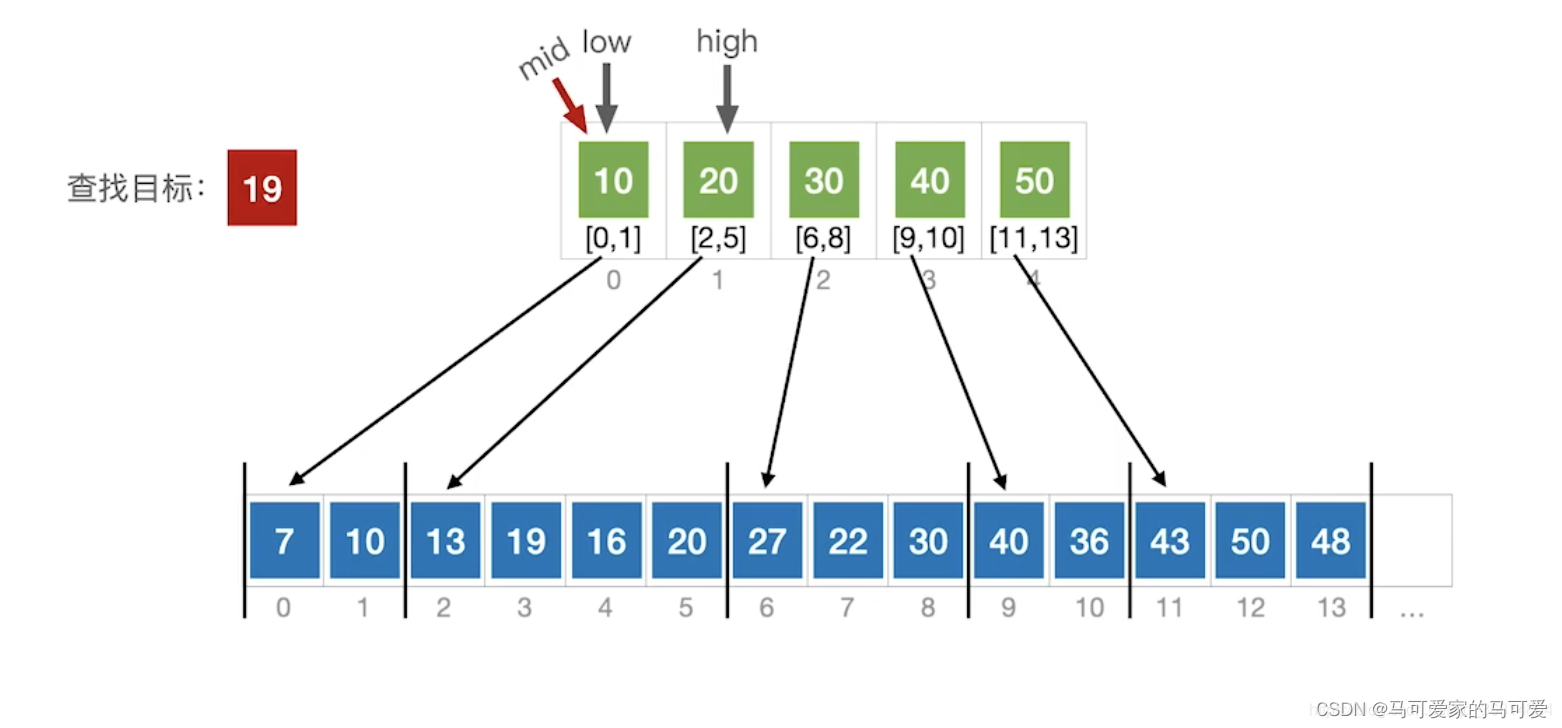
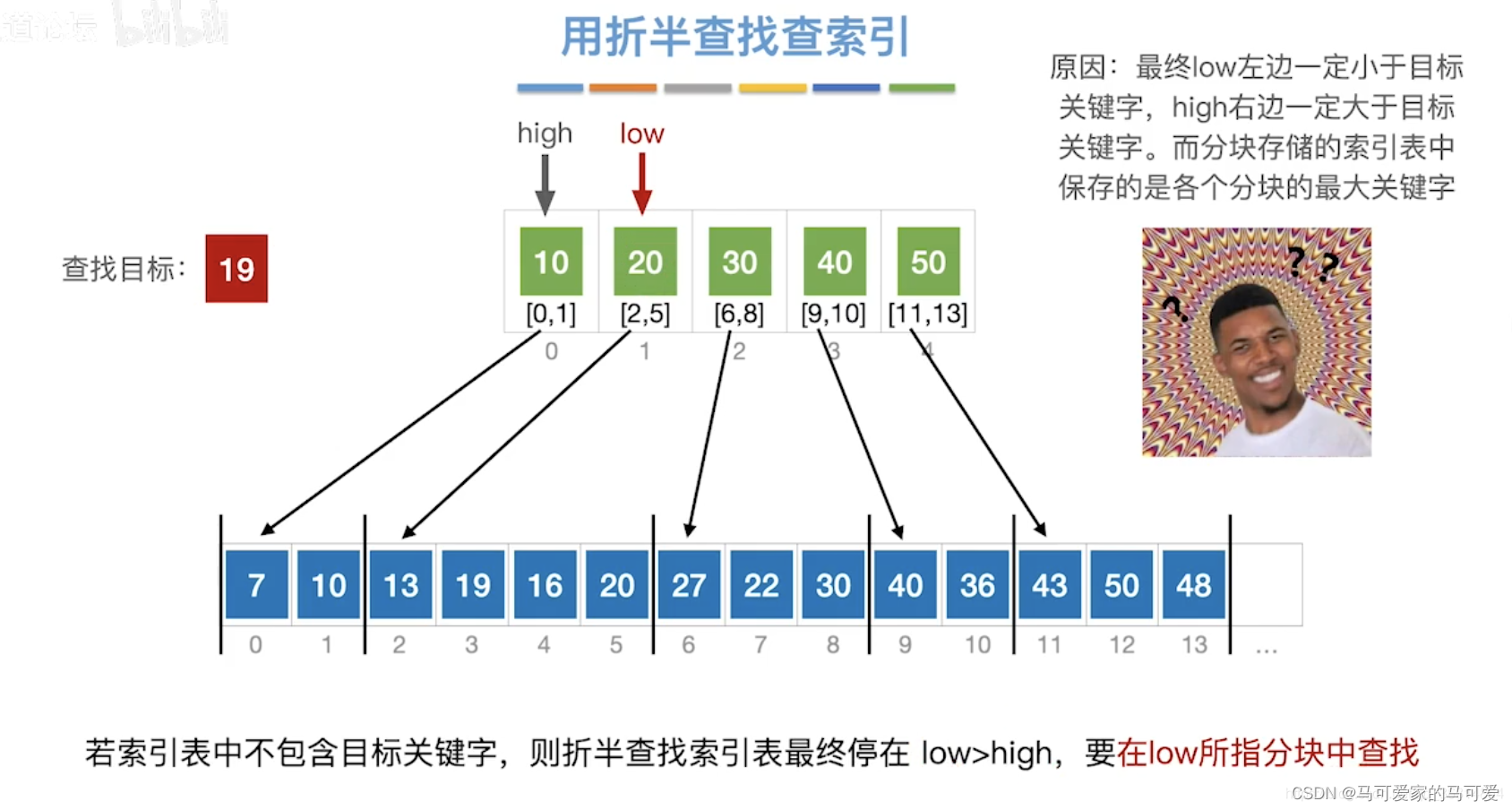
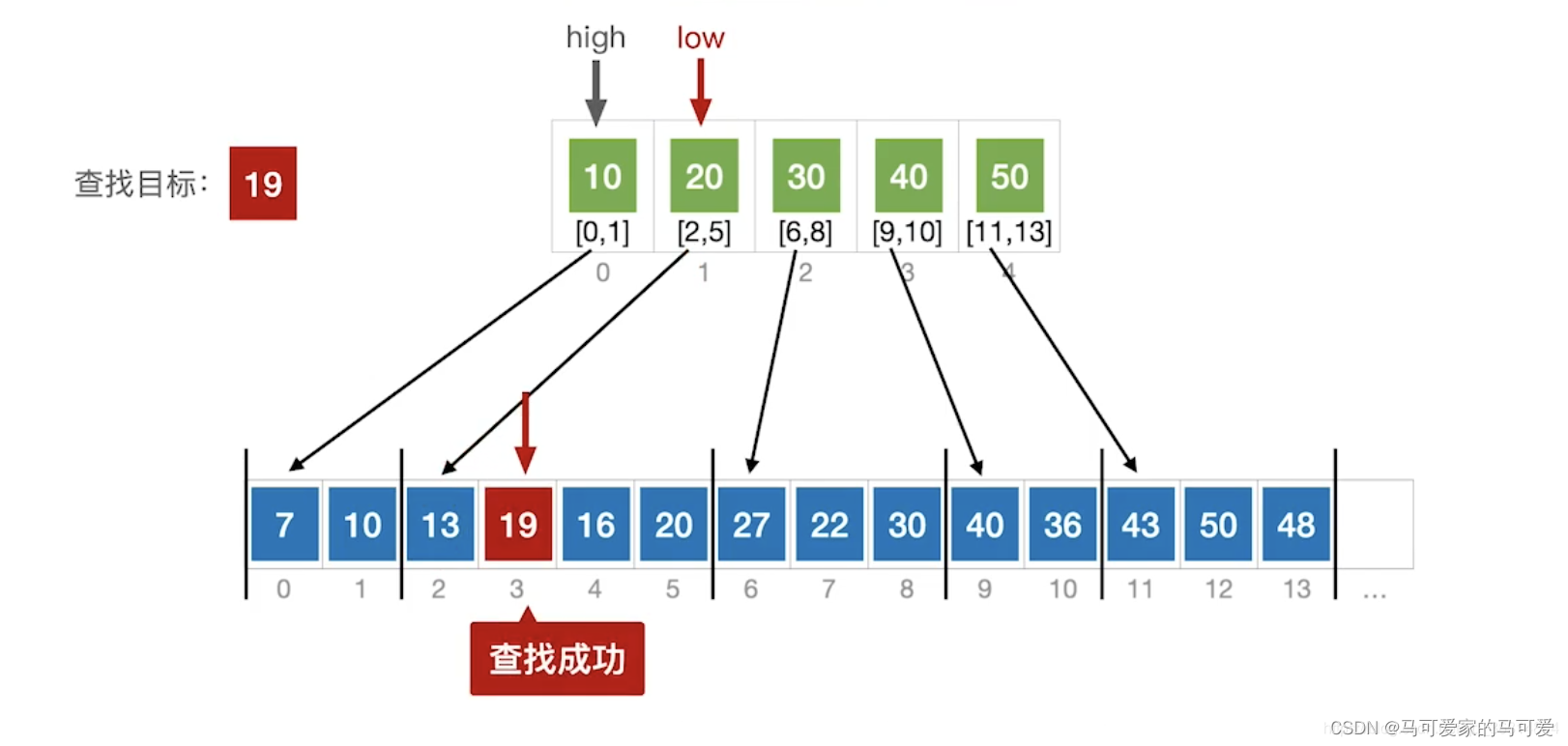
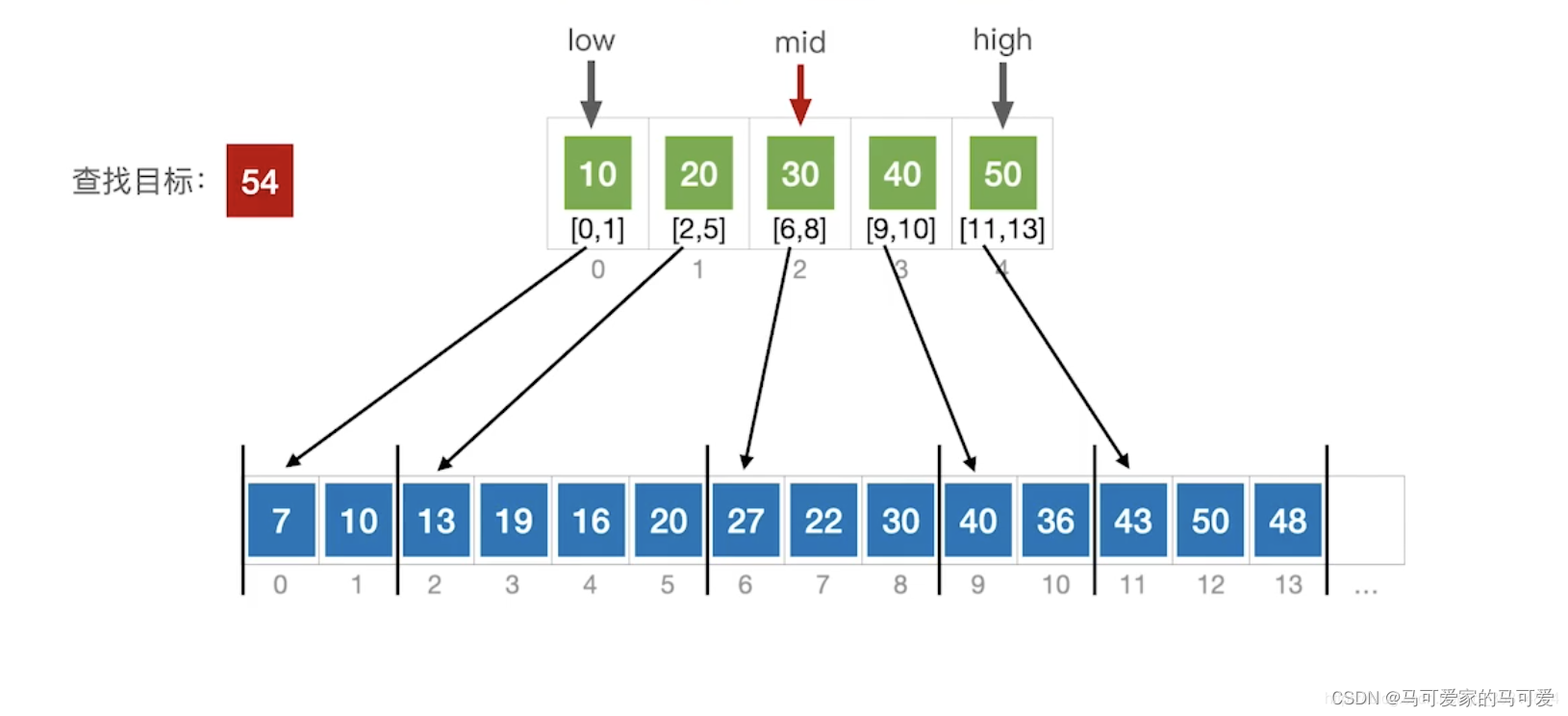
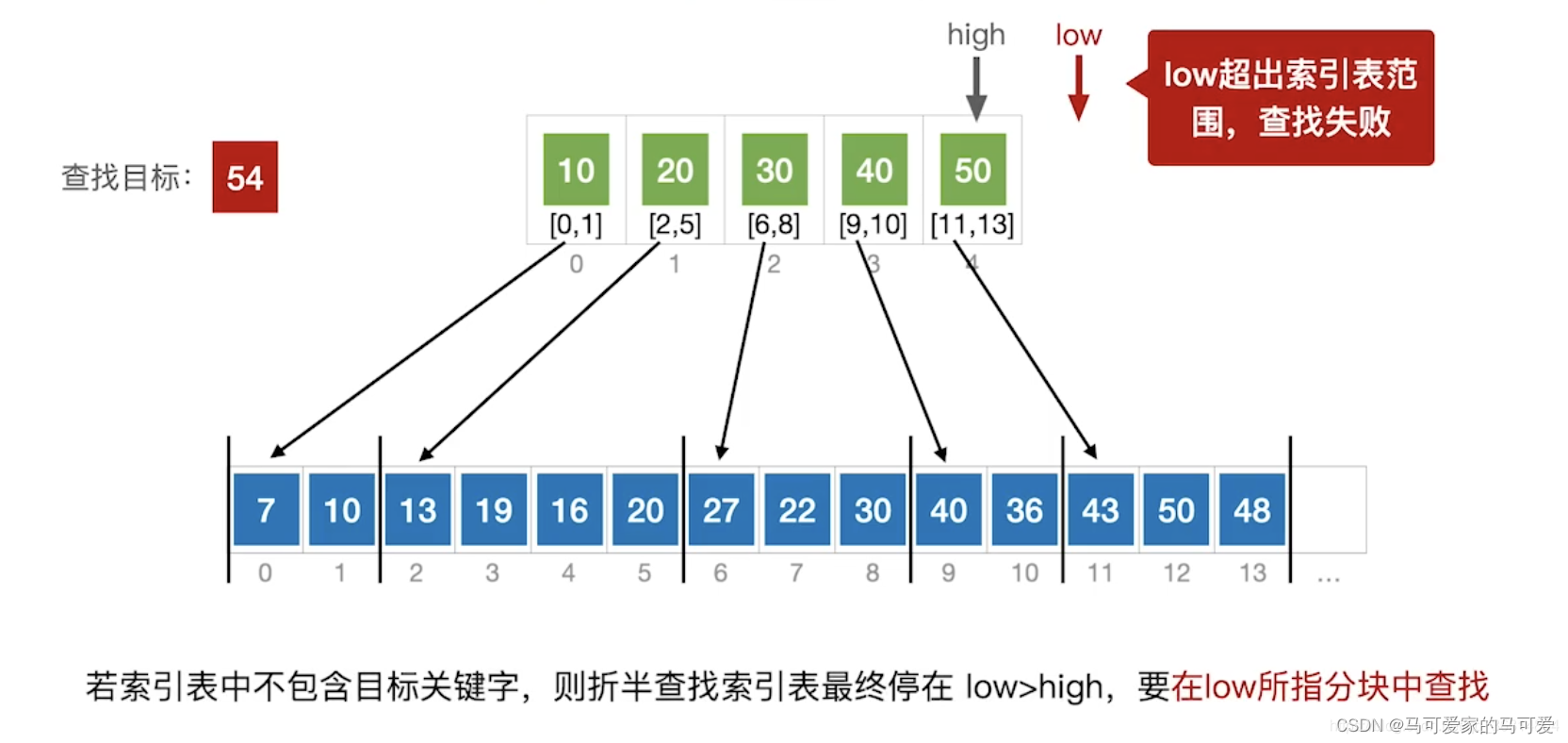
(4)、ASL分析
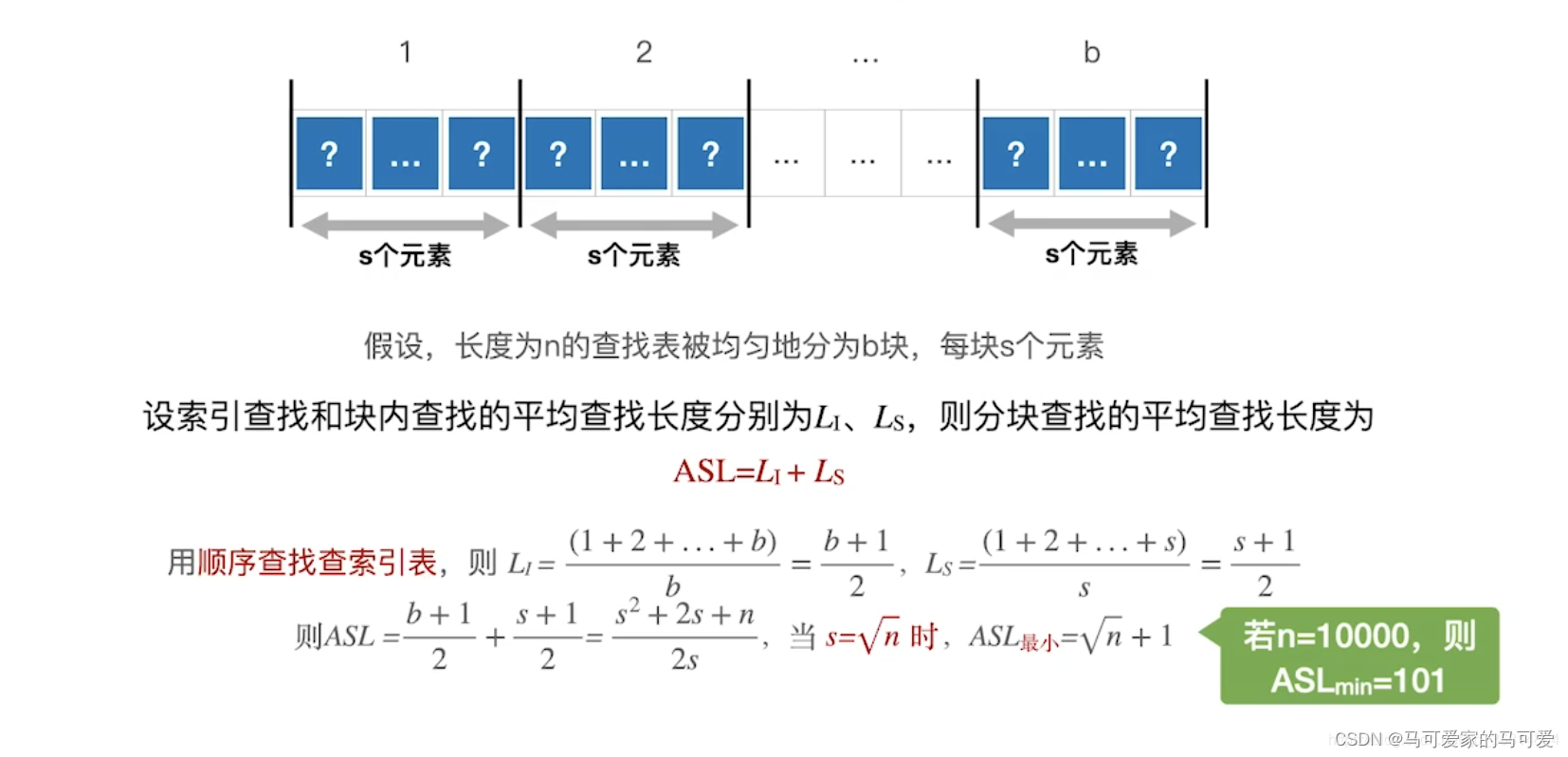
当 s 取根号n的时候,ASLmin = 根号n + 1,This value is a big improvement over sequential lookups,But it's nowhere near as good as a halved search!
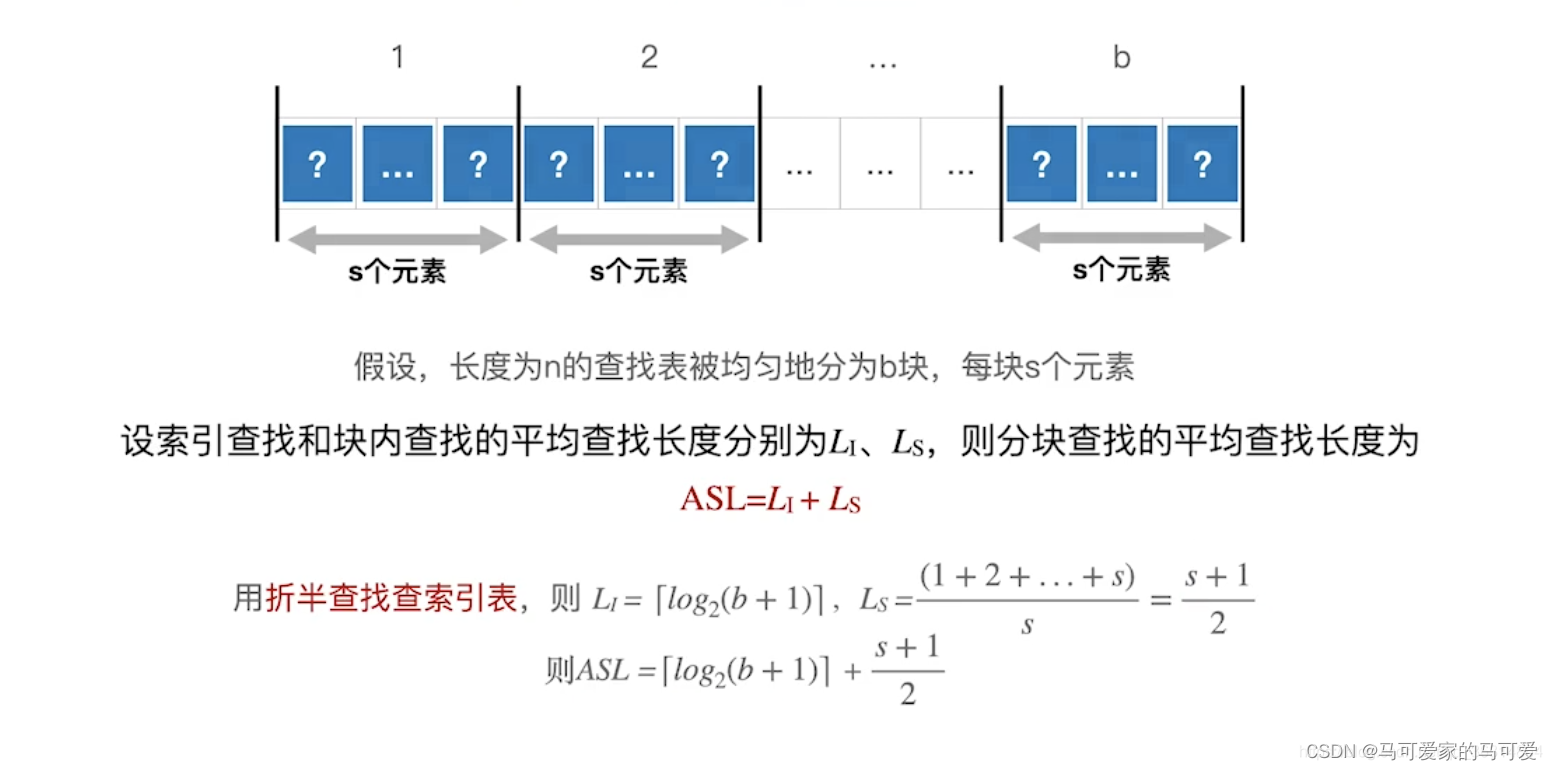
Yan Weimin Edition Data Structures and Algorithms ASL = log2[n/s + 1] + s/2 = log2[b + 1] + s/2,It's a little different from the king's way!
(5)、算法分析
When inserting or deleting data from a table,只要找到该元素对应的块,Insert or delete operations can be performed within the block.由于块内是无序的,Therefore, it is easier to insert or delete,无需进行大量的移动.If the linear table needs to achieve fast search and dynamic changes of frequent insertion or deletion,You can use block search,Because you can use halved search between blocks(二分查找),The unordered block can be inserted or deleted,A lot of movement is not required!
边栏推荐
猜你喜欢
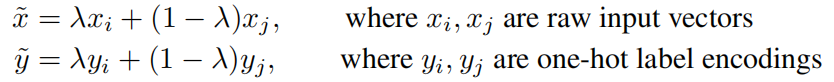
Data to enhance Mixup principle and code reading
nodeJs--封装路由
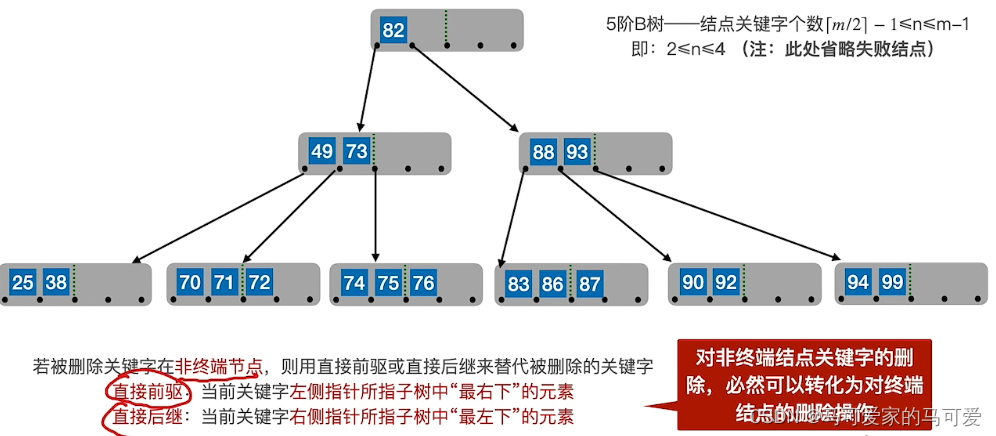
tree table lookup
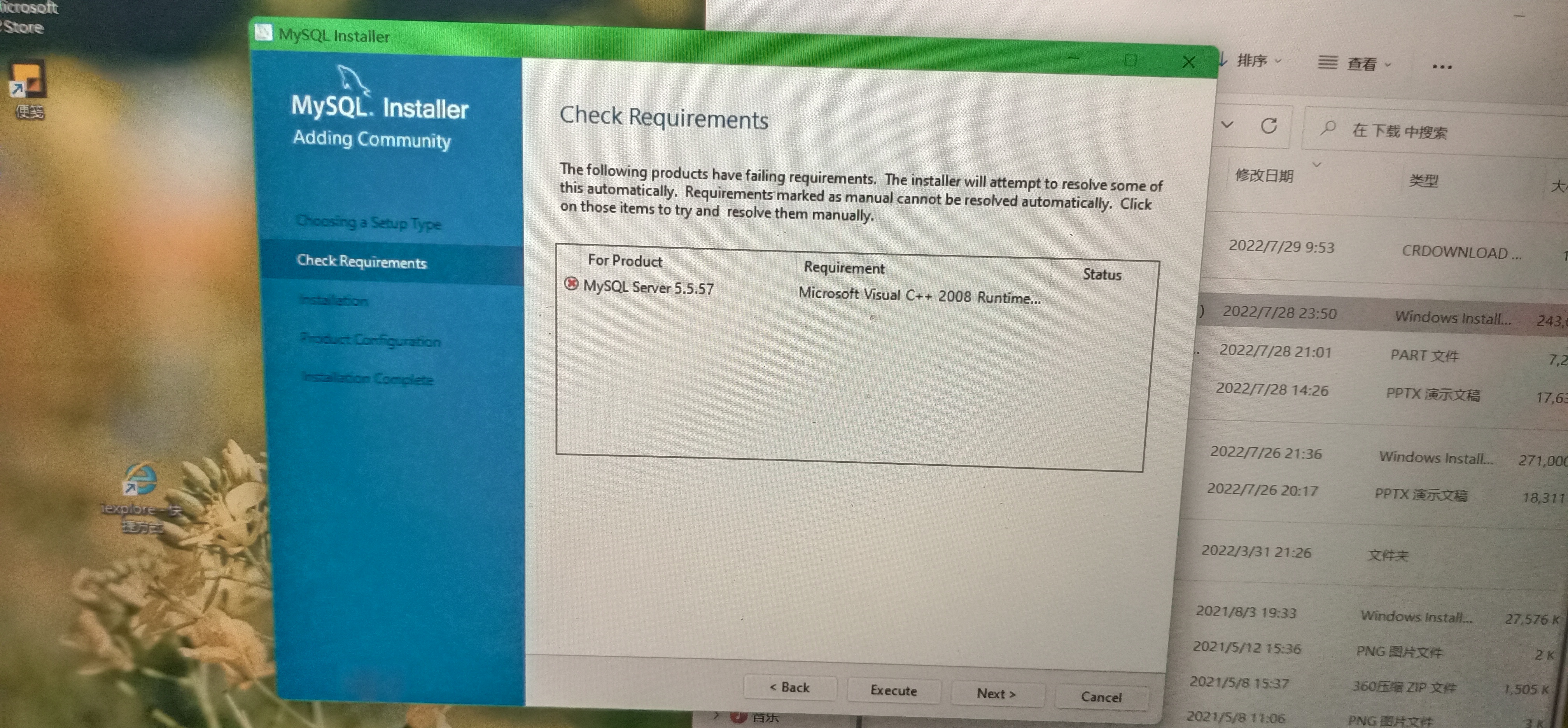
mysql没法Execute 大拿们求解

Compressed storage of special matrices
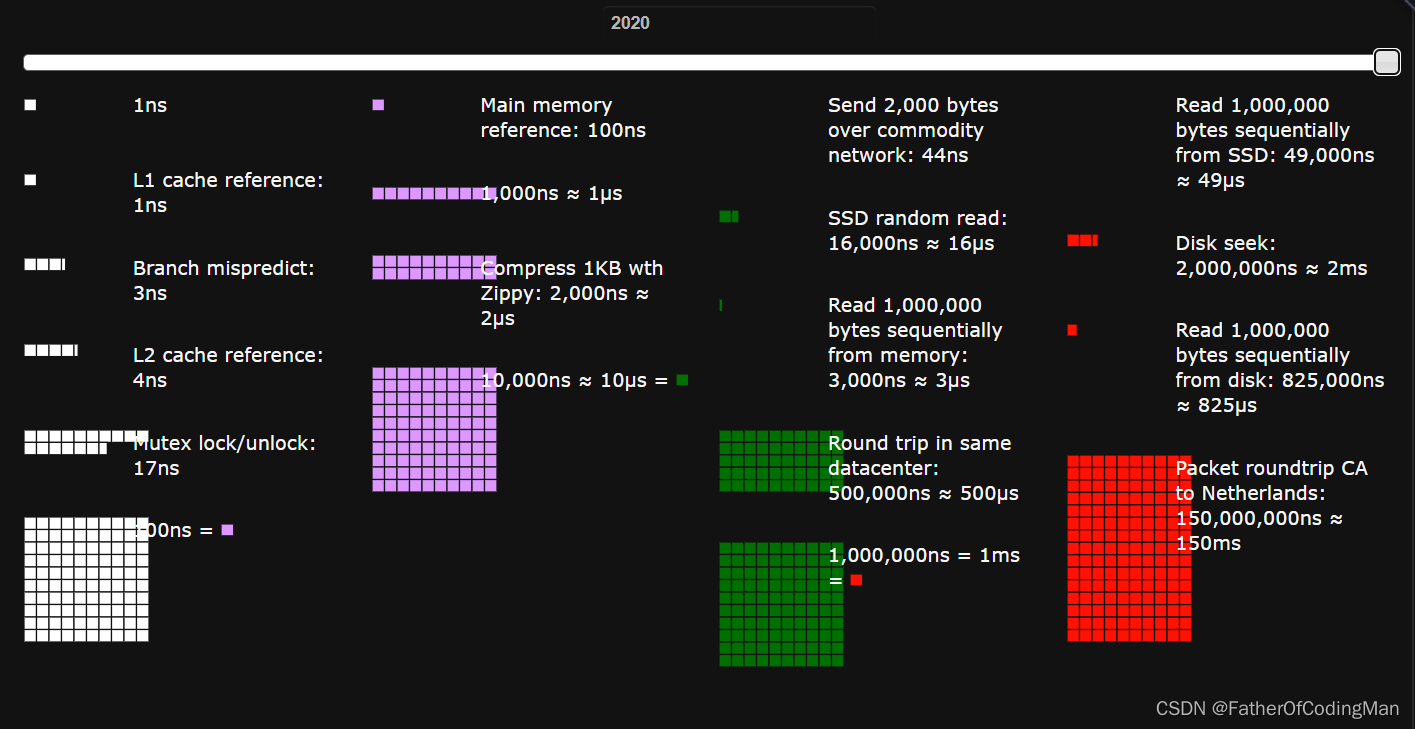
常见的硬件延迟

Unleashing the engine of technological innovation, Intel joins hands with ecological partners to promote the vigorous development of smart retail

How Jin Cang database correctness verification platform installation file

正则表达式,匹配中间的某一段字符串
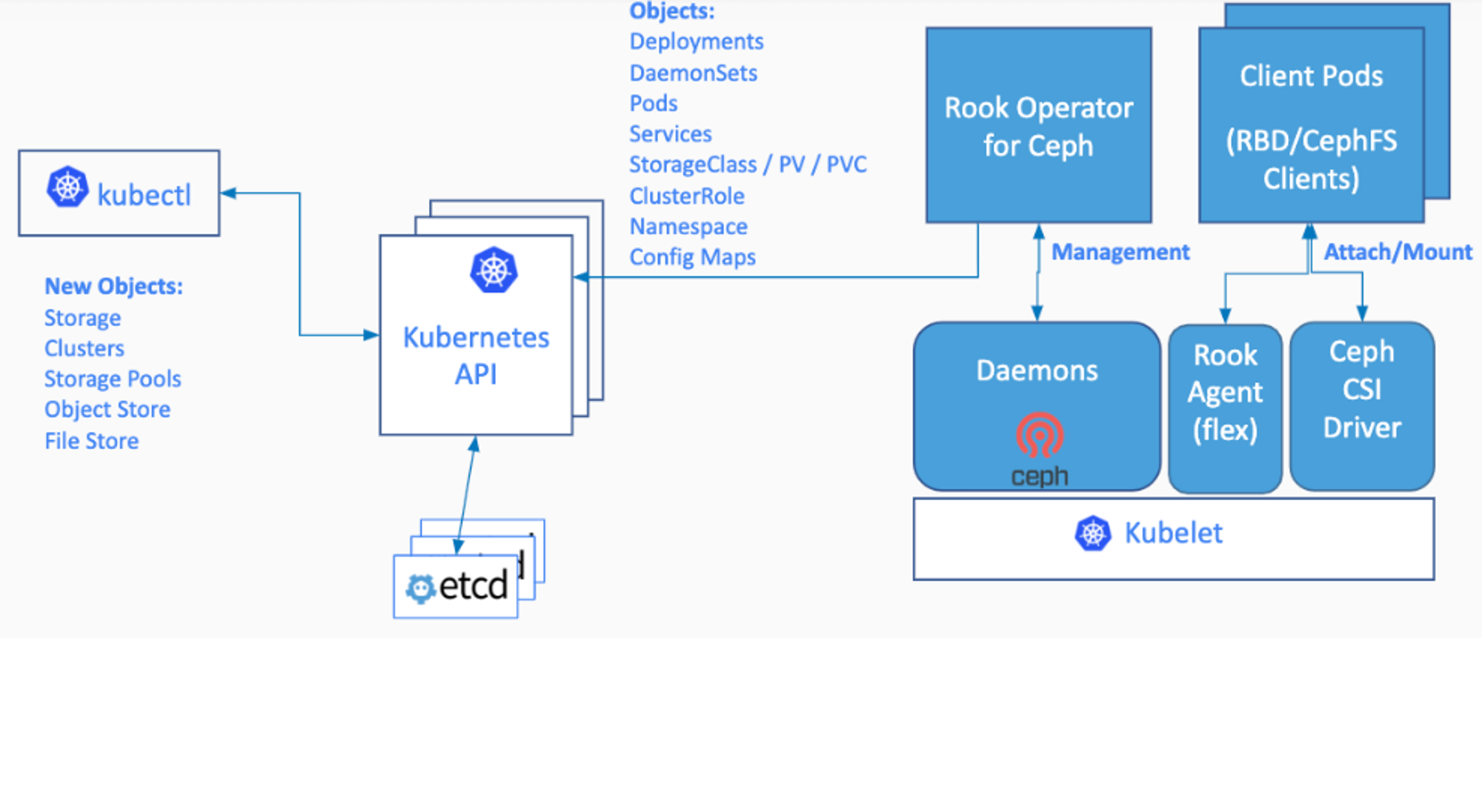
云原生(三十二) | Kubernetes篇之平台存储系统介绍
随机推荐
Common hardware delays
继承关系下构造方法的访问特点
OpenGL 工作原理
数据增强Mixup原理与代码解读
Review 51 MCU
[C language] Detailed explanation of stacks and queues (define, destroy, and data operations)
学习笔记-----左偏树
undo问题
[深入研究4G/5G/6G专题-51]: URLLC-16-《3GPP URLLC相关协议、规范、技术原理深度解读》-11-高可靠性技术-2-链路自适应增强(根据无线链路状态动态选择高可靠性MCS)
【 2 】 OpenCV image processing: basic knowledge of OpenCV
[Decryption] Can the NFTs created by OpenSea for free appear in my wallet without being chained?
行业案例|世界 500 强险企如何建设指标驱动的经营分析系统
开源协议说明LGPL
Go 微服务开发框架 DMicro 的设计思路
[In-depth study of 4G/5G/6G topic-51]: URLLC-16-"3GPP URLLC related protocols, specifications, and technical principles in-depth interpretation"-11-High reliability technology-2-Link adaptive enhancem
ARM Mailbox
Introduction to SDC
链表的简单描述及代码的简单实现
undo problem
2022-08-04:输入:去重数组arr,里面的数只包含0~9。limit,一个数字。 返回:要求比limit小的情况下,能够用arr拼出来的最大数字。 来自字节。