第三十章：普通树的存储和遍历

 前置知识：树的概念、向量（vector）

为了保证学习效果，请保证已经掌握前置知识之后，再来学习本章节！

学习目标

• 了解树的几种存储方法的思想、实现方式和各自的优缺点
• 掌握树的存储方法的代码实现
• 掌握树的两种遍历方式：先根遍历（DFS）和层次遍历方式（BFS）

引入

显然 树 的定义是递归的， 是一种递归的数据结构。树作为一种逻辑结构，同时也是一种 分层 结构，具有以下两个特点：

1）树的根结点没有前驱结点，除根结点之外的所有结点有且只有一个前驱结点。

2）树中所有结点可以有零个或多个后继结点。

有根树的存储

父亲表示法

除根节点外，其他结点有且仅有一个父结点，因此，我们可以把每一条树边存储在其子结点上，形式为：ii 结点的父亲是 jj 结点，如下图所示。

父亲表示法的存储结构基本实现代码如下：

int fa[N];
fa[a] = 0;     // 表示 a 是根，也可用 -1 表示父结点不存在，具体取决于代码的写法
fa[x] = y;     // 连接 x 和 y，结点 x 的父结点是 y

Copy

如果需要保存结点信息，那么可以定义成结构体实现：

struct node{
    int data;            // 结点信息，也可能是其他数据类型
    int father;          // 父结点编号
}
node tree[N];            // 定义一棵树
void link(int x, int y)  // x 的父结点是 y
{
    tree[x].father = y;  // 连接 x 和 y
}

Copy

优点：省空间，并且对于任意结点，可以方便找到其父结点；

缺点：找子结点很麻烦，需要遍历所有结点；

父亲表示法最省空间，后面学习的“并查集”就是采用此法保存树上的父子关系。

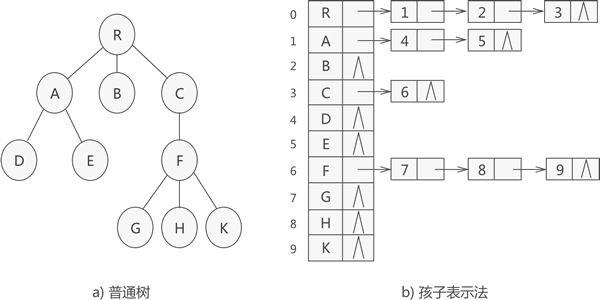
孩子表示法

对于每个结点，有一个数据域和多个指针域，数据域保存当前结点的数据，指针域的每个指针指向一个孩子结点 ，例如下图：

结构体写法示例代码如下：

struct node{
    int data;                // 结点信息，也可能是其他数据类型
    vector<int> children;      // 所有子结点编号
}
node tree[N];                // 定义一棵树
void link(int x, int y)      // x 的父结点是 y
{
    tree[y].children.push_back(x);  // 连接 x 和 y
}

Copy

优点：对于任意结点，可以方便找到其所有子结点；

缺点：找父结点很麻烦，需要遍历所有结点；

父亲孩子表示法

综合上面的两种表示方法的优点，每个结点除了保存结点自身信息外，同时保存当前结点的父结点和孩子结点信息，示例代码如下：

struct node{
    int data;                // 结点信息，也可能是其他数据类型
    int father;              // 父结点编号
    vector<int> children;      // 子结点列表
}
node tree[N];                // 定义一棵树
void link(int x, int y)      // x 的父结点是 y
{
    tree[x].father = y;      // 连接 x 和 y
    tree[y].children.push_back(x);  // 连接 y 和 x
}

Copy

如果在问题中，需要同时知道一个结点的父结点和子结点，则可以采用这种写法。

孩子兄弟表示法*

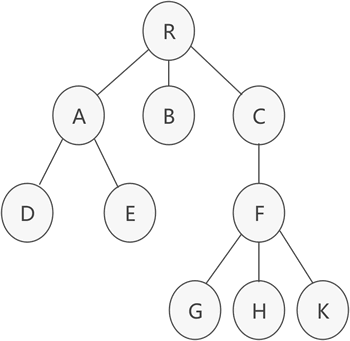
树结构中，位于同一层的节点之间互为兄弟节点。例如，上图的普通树中，节点 A、B 和 C 互为兄弟节点，而节点 D、E 和 F 也互为兄弟节点。

孩子兄弟表示法，采用的是链式存储结构，其存储树的实现思想是：从树的根节点开始，依次用链表存储各个节点的孩子节点和兄弟节点。

因此，该链表中的节点应包含以下 3 部分内容（如下图所示）：

1. 节点的值；

2. 指向孩子节点的指针；

3. 指向兄弟节点的指针；

示例代码如下：

struct node{
    int data;                // 结点信息，也可能是其他数据类型
    node* children;        // 孩子们
    node* brothers;      // 兄弟们
}

Copy

下图是上面的例图中的树使用孩子兄弟表示法进行存储的结果，可以发现，使用孩子兄弟表示法表示的普通树在存储上已经被转化为一棵二叉树存储了，因此可以得出这样一个结论，即通过孩子兄弟表示法，任意一棵普通树都可以相应转化为一棵二叉树，换句话说，任意一棵普通树都有唯一的一棵二叉树于其对应。

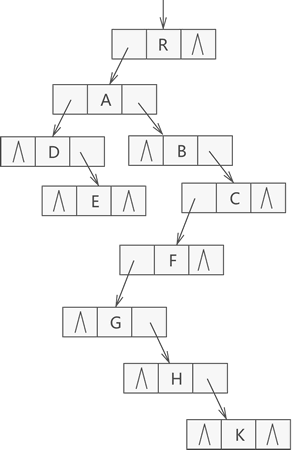
因此，孩子兄弟表示法可以作为将普通树转化为二叉树的最有效方法，通常又被称为"二叉树表示法"或"二叉链表表示法"。

有根树的图存储方式*

树其实是一种特殊的图，可以把一条树边看作一条父亲指向儿子（或儿子指向父亲）的有向边。因此图的存储方式也可用来存储树。图的存储有邻接矩阵、邻接表和链式前向星（特殊的邻接表）等实现方式。具体做法将在后面学习，这里只做简单说明。

邻接矩阵

使用一个 n×nn×n 的 bool 数组 mpmp，mp[x][y]mp[x][y] 为 true 则表示 x 到 y 存在有向边，反之则表示不能存在该有向边。

邻接矩阵存储代码如下：

bool mp[N][N];
void link(int x, int y)
{
    mp[x][y] = 1;   // x 到 y 存在有向边
}

Copy

邻接表

同样，我们可以采用邻接表来存储一个点连出的多条树边，如下图所示。

使用 C++ 的 STL 向量容器 vector 的邻接表存储代码如下：

vector<int> g[N];    // g[i] 存和结点 i 的出边

void link(int x, int y)  // 连一条由 x 指向 y 的边，在树中指 x 是 y 的父结点
{
    g[x].push_back(y);
}

Copy

链式前向星*

链式前向星其实就是静态建立的邻接表，时间效率为 O(m)O(m)，空间效率也为 O(m)O(m)，遍历效率也为 O(m)O(m)，mm 表示边的数量。链式前向星存各种图都很适合，但不能快速查询一条边是否存在，也不能方便地对一个点的出边进行排序。

链式前向星存树的示例代码如下：

int cnt;            // 边的总数量
struct node{
    int to;         // 存储当前边指向的儿子的编号
    int next;       // 指向当前儿子的下一个兄弟
} edge[N];          //
int head[N];        // 存储结点的最后一个儿子的编号

void link(int x, int y)
{
    edge[cnt].to = y;
    edge[cnt].next = head[x];
    head[x] = cnt++;
}

Copy

无根树的图存储*

因为无根树没有确定的根，因此树中的树边是没有明确的父子之分的，也就没有明确的方向。所以无根树的存储一般用无向图的方式进行存储。在存图时，每连接一条边，要同时存储相应的两条边。示例代码如下：

int cnt;            // 边的总数量
struct node{
    int to;         // 存储当前边指向的儿子的编号
    int next;       // 指向当前儿子的下一个兄弟
} edge[N*2];
int head[N];        // head[i]: 结点 i 的最后一个儿子的编号

void link(int x, int y)
{
    edge[cnt].to = y;
    edge[cnt].next = head[x];
    head[x] = cnt++;
}

Copy

树的遍历

定义

树的遍历是指从根节点出发，按照某种次序依次访问树中的所有结点，使得每个结点仅被访问一次。常用的遍历方式有：先根遍历（DFS）和层次遍历（BFS）。

先根遍历

遍历规则：

1. 若树为空，则停止遍历；

2. 如果树不为空，否则先访问根结点，再依次先根遍历根结点的所有子树。

可以看出，先根遍历是一种深度优先遍历。

代码框架：

// 深度优先遍历树
void dfs(int root)
{
    // 1- 对当前结点进行处理，比如输出
    ......
    // 2- 扩展新结点，即遍历所有子节点
    for(int i = 0; i < tree[root].son.size(); i++)
    {
        dfs(tree[root].son[i]);  // 子节点入“函数栈”
    }
}

Copy

层次遍历

遍历规则：

1. 若树为空，则停止遍历。

2. 如果树不为空，则从树的第一层，也就是根节点开始访问，从上而下逐层访问，在同一层中，按照从左到右的顺序对节点逐个访问。

如果某个结点先被访问，则其子节点也会先被访问，如果将访问本身看作入，将访问子节点看作出，则层次遍历的规则满足先进先出。

可以看出，层次遍历是一种广度优先遍历。

代码框架：

void bfs(int root)
{
    queue<int> q;        // 1- 定义队列
    q.push(root);        // 2- 根节点入队
    while(!q.empty())    // 3- 只要队列不空，就：
    {
        // (1) 取出队首结点，并对当前结点进行处理，比如输出
        int k = q.front();      
        q.pop();
        ......
        // (2) 扩展新结点，即遍历所有子结点
        for(int i = 0; i < tree[k].son.size(); i++)
        {
            q.push(tree[k].son[i]);  // 子结点入队
        }
    }
}

Copy

总结

1、树的存储方法比较多，每种方法各有优缺点，对比如下：

	双亲或孩子表示法	双亲孩子表示法	邻接矩阵	邻接表	链式前向星
优点	理解容易，存储消耗空间最小	理解容易	实现简单	实现简单，消耗空间较小，各种场合都适用	消耗空间小，各种场合都适用
缺点	存储的信息量少，很多操作不便	同时存父子结点，空间消耗较大O(2n)O(2n)	消耗空间巨大，O(n^2)O(n2)，适合稠密图	需熟练掌握 vector 操作	较难理解，不能迅速查询边和对一个点的出边排序

2、树的遍历则深刻体现出深度优先搜索和广度优先搜索的重要性。DFS 和 BFS 在树中应用很多，一定要熟练掌握。

练习题目

P2728 找树根和孩子

P2732 找双亲和孩子

P2733 寻找堂兄弟

P2801 树的深度优先遍历

P2802 树的广度优先遍历

P2803 树上结点的深度

P2506 普通树的高度