当前位置:网站首页>【ONE·Data || 排序入门】
【ONE·Data || 排序入门】
2022-08-02 13:27:00 【执鹤千山】
总言
排序入门(C语言)。
文章目录
插入排序
1、直接插入排序
//直接插入排序
//时间复杂度O(N^2),最好的情况O(N)
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)//i<n-1,默认end < n,end+1为插入数,因此end+1<n,既有end <n+1,i是用来控制end遍历总元素的
{
//单趟插入排序:默认[0,end]有序,新的需要插入的数在下标为end+1的位置,保持插入后仍旧保持有序
int end = i;
int tmp = a[end + 1];//此处的end+1与while循环中的end+1作用不同,此处的end+1为单趟中新插入的元素,tmp保存它是为了与原先元素作对比
while (end >= 0)//while循环,或者说end实际在遍历原先元素,以便tmp与end所处下标的元素作对比
{
if (tmp < a[end])//排升序:tmp需要放到end、end+1之间,即a[end]≤tmp≤a[end+1]
{
a[end + 1] = a[end];//正因如此,要把end后方的位置空出,以便tmp插入,故有将当前end所处位置元素往end+1处挪动,并更新end指向这一操作
end--;
}
else
{
break;//此处直接跳出是便于当end下标为-1时与下标>0时同一赋值
}
}
a[end + 1] = tmp;
}
2、希尔排序(缩小增量排序)
①写法一
//希尔排序·写法一
void ShellSort(int* a, int n)
{
int gap=3;//gap的值在这种写法中需要给定
//多组间的流动:
for (int j = 0; j < gap; j++)
{
//单组:如何对同组中的成员进行排序,有 end+gap < n 既end < n-gap。
//ps:同gap下的多组,更换到别组时end < n-gap 条件仍旧成立。
for (int i = j; i < n - gap; i+=gap)
{
//单趟:其思路和直接插入排序类似,只是跨步由gap=1变为了任意正整数
int end = i;
int tmp = a[end + gap];//与直接插入排序相比,此处tmp储存的是与end相距跨步为gap的元素:即同一组元素
while (end >= 0)
{
if (tmp < a[end])//排升序:当下标为end+gap的元素比下标为end所指向的元素还小时,将下标为end出的元素往后挪,挪到end+gap下标处
{
//此处的道理和普通插入排序相似,只是跨步不同。类似于周期为π的傅里叶级数和周期为l的傅立叶级数。
a[end + gap] = a[end];
end -= gap;//注意此处end的跨步也为gap
}
else
{
break;
}
a[end + gap] = tmp;
}
}
}
}
②写法二
//希尔排序·写法二
void ShellSort2(int* a, int n)
{
int gap = 3;
for (int i = 0; i < n - gap; i++)//若此处换为i++,则是多组元素轮番进行排序,即交替分组插入排序
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
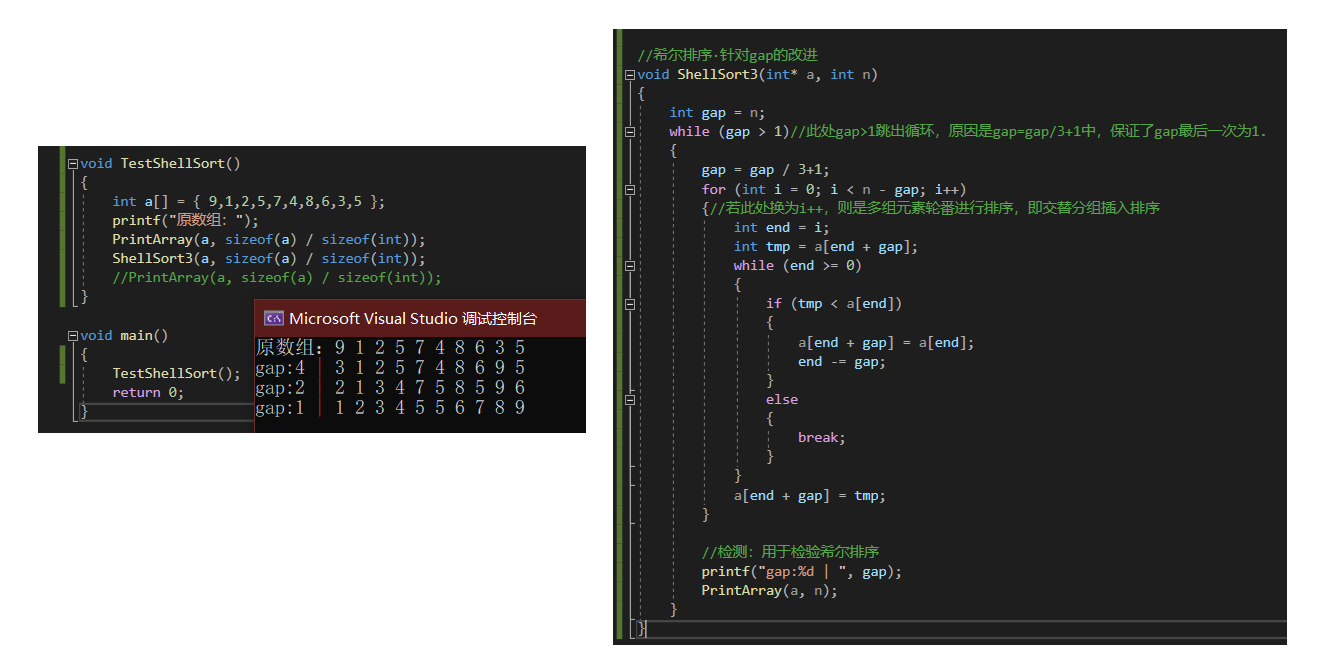
③针对gap的改进
//希尔排序·针对gap的改进 平均:O(N^1.3)
void ShellSort3(int* a, int n)
{
int gap = n;
while (gap > 1)//此处gap>1跳出循环,原因是gap=gap/3+1中,保证了gap最后一次为1.
{
gap = gap / 3+1;
for (int i = 0; i < n - gap; i++)
{
//若此处换为i++,则是多组元素轮番进行排序,即交替分组插入排序
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
//检测:用于检验希尔排序
printf("gap:%d | ", gap);
PrintArray(a, n);
}
}
选择排序
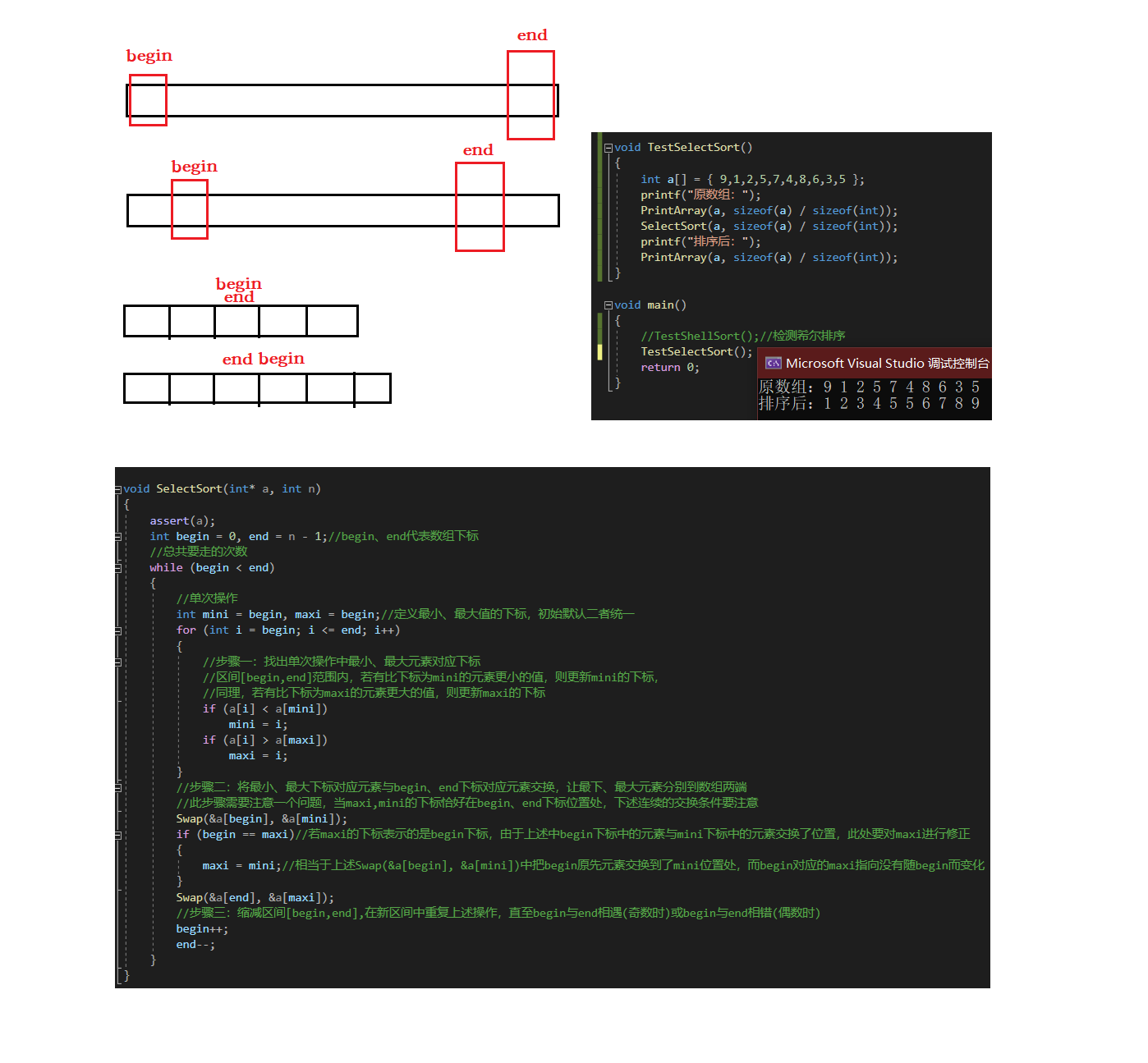
1、直接选择排序
//直接选择排序:时间复杂度O(N^2),最好的情况是O(N^2)
//对比:与直接插入排序相比,谁更好?(直接插入排序相对更佳)
//直接插入排序在接近有序时时间复杂度为O(N),最坏的情况为O(N^2),直接选择排序没有这种优势,
//其时间复杂度不会随所给数据的有序性或其它性质而改变,严格意义上遵循等查数列
void SelectSort(int* a, int n)
{
assert(a);
int begin = 0, end = n - 1;//begin、end代表数组下标
//总共要走的次数
while (begin < end)
{
//单次操作
int mini = begin, maxi = begin;//定义最小、最大值的下标,初始默认二者统一
for (int i = begin; i <= end; i++)
{
//步骤一:找出单次操作中最小、最大元素对应下标
//区间[begin,end]范围内,若有比下标为mini的元素更小的值,则更新mini的下标,
//同理,若有比下标为maxi的元素更大的值,则更新maxi的下标
if (a[i] < a[mini])
mini = i;
if (a[i] > a[maxi])
maxi = i;
}
//步骤二:将最小、最大下标对应元素与begin、end下标对应元素交换,让最下、最大元素分别到数组两端
//此步骤需要注意一个问题,当maxi,mini的下标恰好在begin、end下标位置处,下述连续的交换条件要注意
Swap(&a[begin], &a[mini]);
if (begin == maxi)//若maxi的下标表示的是begin下标,由于上述中begin下标中的元素与mini下标中的元素交换了位置,此处要对maxi进行修正
{
maxi = mini;//相当于上述Swap(&a[begin], &a[mini])中把begin原先元素交换到了mini位置处,而begin对应的maxi指向没有随begin而变化
}
Swap(&a[end], &a[maxi]);
//步骤三:缩减区间[begin,end],在新区间中重复上述操作,直至begin与end相遇(奇数时)或begin与end相错(偶数时)
begin++;
end--;
}
}
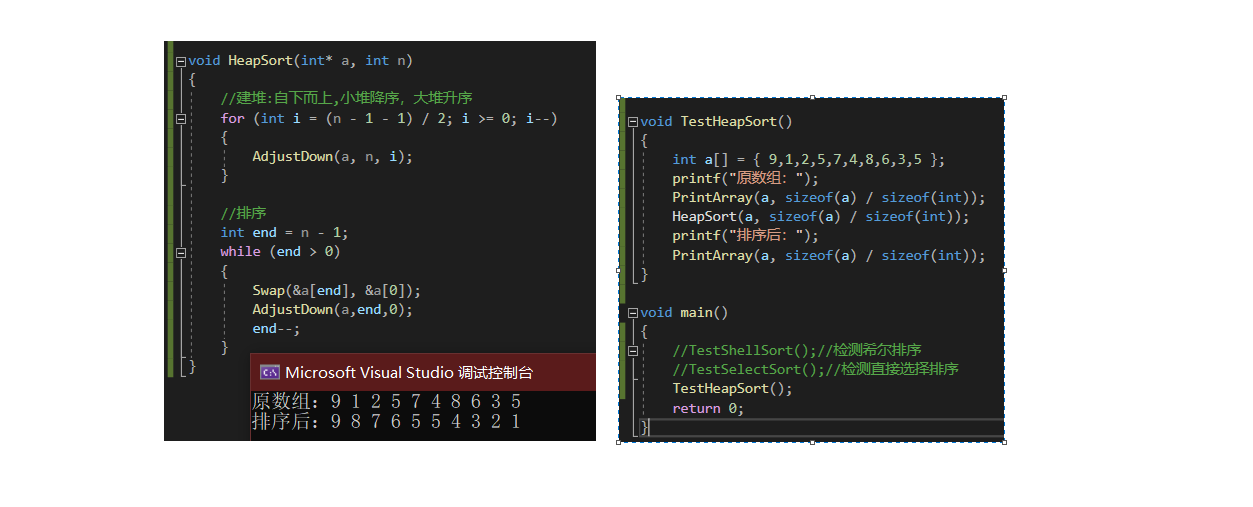
2、堆排序
详细解释文章:数组堆及其延伸应用
//向下调整函数:
void AdjustDown(int*a,int n,int parent)
{
int child = parent * 2 + 1;
while (child<n)
{
//检查左右孩子
if (child+1<n && a[child+1]<a[child])//建小堆
{
child = child + 1;
}
if (a[child] < a[parent])//建小堆
{
//交换
Swap(&a[child], &a[parent]);
//迭代
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//堆排序:选择向下调整函数,时间复杂度为O(N*logN)
void HeapSort(int* a, int n)
{
//建堆:自下而上,小堆降序,大堆升序
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
//排序
int end = n - 1;
while (end > 0)
{
Swap(&a[end], &a[0]);
AdjustDown(a,end,0);
end--;
}
}
交换排序
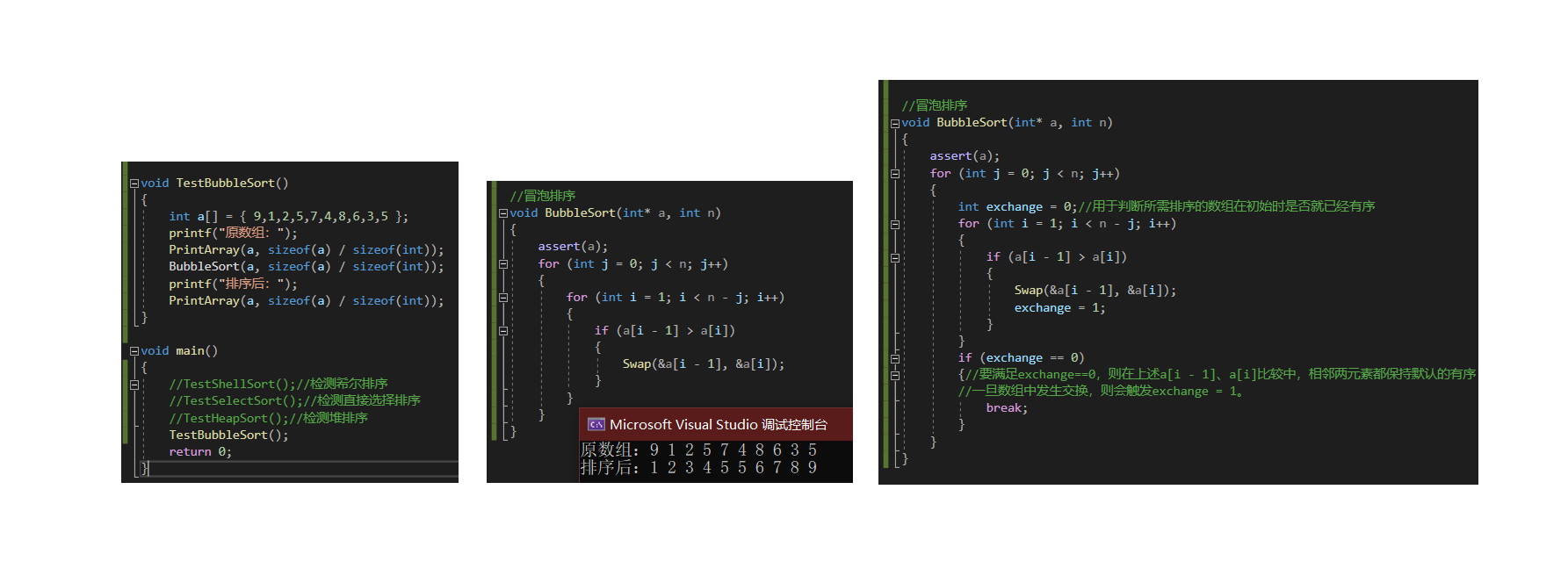
1、冒泡排序
//冒泡排序
//时间复杂度O(N^2),最好的情况是O(N)
//对比直接插入排序,谁更好?(直接插入排序)
//接近有序或局部有序时,直接插入排序在时间复杂度上相对更佳
void BubbleSort(int* a, int n)
{
assert(a);
for (int j = 0; j < n; j++)
{
int exchange = 0;//用于判断所需排序的数组在初始时是否就已经有序
for (int i = 1; i < n - j; i++)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
{
//要满足exchange==0,则在上述a[i - 1]、a[i]比较中,相邻两元素都保持默认的有序
//一旦数组中发生交换,则会触发exchange = 1。
break;
}
}
}
2、快速排序
①hoare版
//快速排序
//时间复杂度:O(NlogN)
void QuickSort(int* a, int begin,int end)//[begin,end]
{
//递归的返回条件
if (begin >= end)//当区间不存在或区间只有一个值时
{
return;
}
//单趟
int left = begin, right = end;//左右下标
int key = left;//选左边为key
while (left < right)
{
//先走右边,右边升序要找小
while (left < right && a[right] >= a[key])
{
//left<right保证了下标不越界问题,
//加入a[left/right]=a[key]的判断保证了left、right能正常向后向前遍历
right--;
}
//再走左边,左边升序要找大
while (left < right && a[left] <= a[key])
{
left++;
}
//左右分别找到对应值,交换
Swap(&a[left], &a[right]);
}
//left、right相遇时,将key处的数据与left处的数据交换
Swap(&a[key], &a[left]);
key = left;
//单趟排序完成,数组被分为三个区间
//[begin,key-1] key [key+1,end]
QuickSort(a, begin, key-1);
QuickSort(a, key + 1,end);
}
快排中的单趟逻辑图示
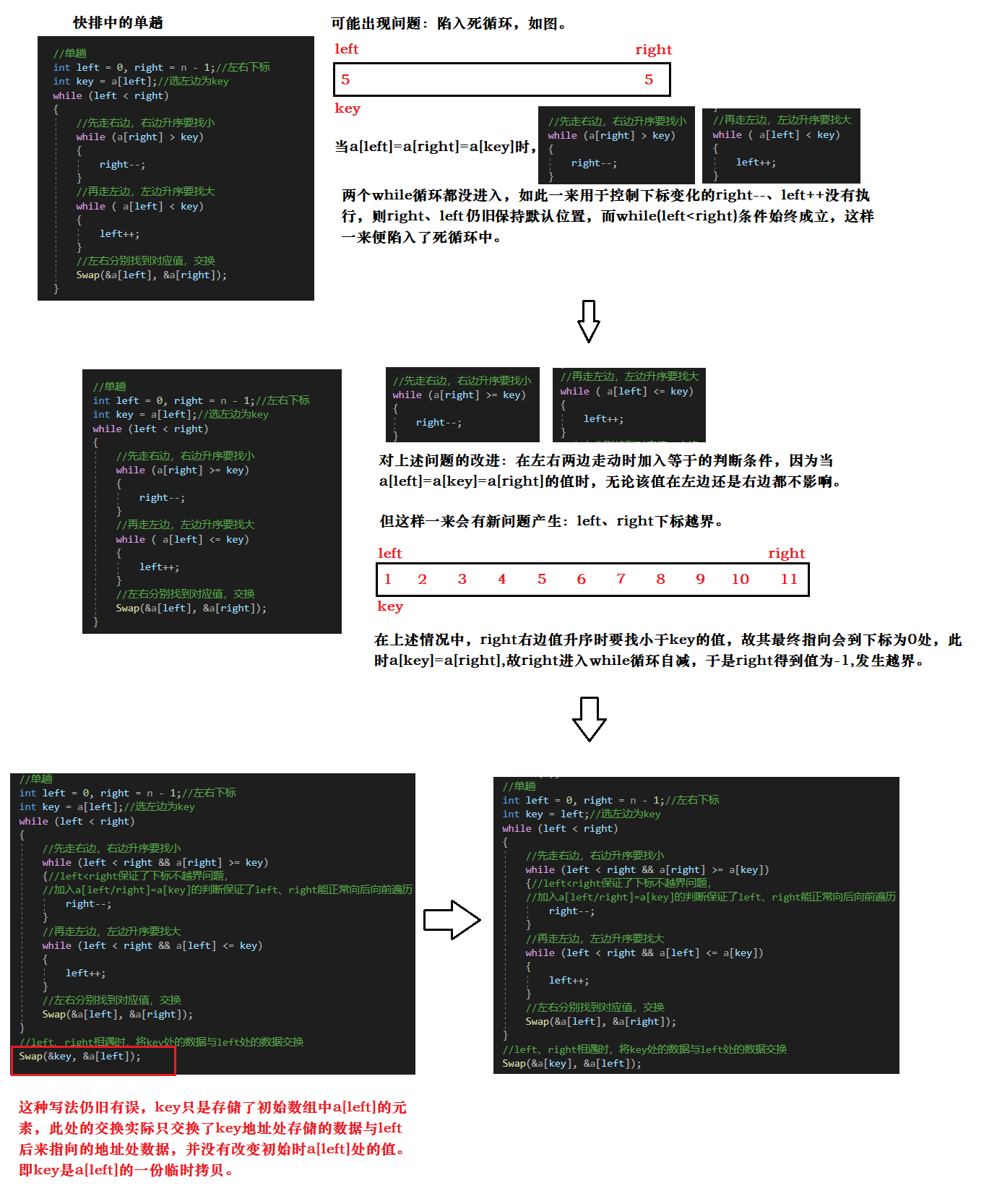
快排中的单趟文字表述
思路: 选出一个key,一般是最左边或者最右边的值。
单趟排序完成后,对于升序,要求达到左边比key小,右边比key大,对降序,要求达到左边比key大,右边比key小。
对于单趟(升序):
先以最左或最右位置选出一个key,设左为L,右为R。
R先向前移动,找比key小的位置,R找到小于key的位置,保持不动,L再向后移动,找比key大的位置,找到之后,交换R和L位置的数值。
R再次向前移动,找比key小的位置,L向后移动,找比key大的位置,找到之后,交换R和L位置的数值。
R继续向前找比key小的值,L继续向后找比key大的值,当R和L相遇,将该位置处的值与key的值交换结束。
此时key左边的值都比key小,key右边的值都比key大。
1、如何做到左边数值比key小,右边数值比key大?
回答:将左边比key大的值和右边比key小的值两两交换,这样左边只剩下原先比key小的值和被交换过来的比key小的值,右边与左边相反。
如此便达到升序的效果。如果要实现降序,只需要左边找小值,右边找大值即可。
2、关于左右L、R是否会错过问题?
回答:不会,L、R会错过的情况是二者同时一个向后一个向前遍历,因奇偶数的不同而导致相错问题。
但此处L、R并非同时进行,是一个先完成它的步数,另一个再完成对应步数,由于二者相向,故一定会有L=R相遇时。
3、左边做key,为什么要让右边先走?(反之,右边做key,为什么要让左边先走?)
回答: 对于升序,左边做key右边先走,可保证相遇时的值比key小或者与key相等(右边做key左边先走,可保证相遇时的值比key大,或者与key相等)
分析: 以升序、左边做key右边先走为例子
情形一: R先走,R停下,L去遇到R(L停下只有两种可能,L找到对应值停下,L与R相遇,此处是后者)。
此时相遇的位置是R停下的位置,而要使R停下,即有a[R]<a[key]。相遇交换就使得小于key的值到左边去。
情形二: R先走,R没有找到比key要小的值,R去遇到了L。
子情形一,最初始的一轮循环中,R往前走直接到达key处(即L没有机会往后走),此时说明key后的数组元素都比key大,LR相遇点的值即上述中与key相等的情况。
子情形二,L、R经过彼此交换后的下一组循环中,R往前走直接遇到了L,说明在(L,R]区间内的元素都比key大,而L(与R的相遇点)处的值是上一轮循环后经过交换的值,即上一轮R中小于key的值此时在下一轮循环L位置处(L在R后变动)。
Haore法快排,此处将单趟排序部分封装为一个函数,方便后续使用其它方法时改进。
//快速排序
//单趟排序,以Hoare法实现
int PartSort(int* a, int begin, int end)
{
//单趟
int left = begin, right = end;//左右下标
int key = left;//选左边为key
while (left < right)
{
//先走右边,右边升序要找小
while (left < right && a[right] >= a[key])
{
//left<right保证了下标不越界问题,
//加入a[left/right]=a[key]的判断保证了left、right能正常向后向前遍历
right--;
}
//再走左边,左边升序要找大
while (left < right && a[left] <= a[key])
{
left++;
}
//左右分别找到对应值,交换
Swap(&a[left], &a[right]);
}
//left、right相遇时,将key处的数据与left处的数据交换
Swap(&a[key], &a[left]);
key = left;
return key;
}
//快排
void QuickSort(int* a, int begin,int end)//[begin,end]
{
//递归的返回条件
if (begin >= end)//当区间不存在或区间只有一个值时
{
return;
}
//单趟排序
int key = PartSort(a, begin, end);
//单趟排序完成,数组被分为三个区间
//[begin,key-1] key [key+1,end]
QuickSort(a, begin, key-1);
QuickSort(a, key + 1,end);
}
②挖坑法
先得到第一个数据存放在临时变量key中,形成一个坑位,key=6。
R开始向前移动,找比key的值小的位置,找到后,将该值放入坑位中,该值原先位置形成新的坑位,
L开始向后移动,找比key大的值,找到后,又将该值放入坑位中,再形成新的坑位。
R再次向前移动,找比key小的位置,找到后,将该值放入坑位,该位置形成新的坑位,
L紧接着向后移动,找比key大的位置,找到后,将该值放入坑位中,该位置形成新的坑位。
如此循环翻覆,当L和R相遇时,将key中的值放入坑位中,结束循环。此时坑位左边的值都比坑位小,右边的值都比坑位大。
此法相较于上一种方法,在于提高了理解性,不必纠结于为什么先走右边再走左边。在一轮中,L、R有一个充当了坑位,坑位本身是固定不能移动的,因此只能移动L、R中非坑位的走向。
//快速排序
//单趟排序,以挖坑法实现
int PartSort2(int* a, int begin, int end)
{
int key = a[begin];//保留首位数据
int left = begin, right = end;//左右下标(此步也可直接使用begin、end)
int pit = begin;//用于记录坑位坐标
while (left < right)
{
//左边有坑位,则升序在右边找小的,找到后将数据填入坑中,右边形成新的坑位
while (left<right && a[right]>=key)//left<right防止越界,加入=保证right、left的更迭
{
right--;
}
//若结束上面循环,即意味着右侧找到符合条件的值,将其填入坑位,并更新新的坑位坐标
a[pit] = a[right];
pit = right;
//上述结束后,此时右边有坑位,则升序在左边找大的,找到后将数据填入坑中,左边形成新的坑位
while (left < right && a[left] < key)
{
left++;
}
//若结束上面循环,即意味着左边找到了符合条件的值,将其填入坑位,并更新新的坑位坐标
a[pit] = a[left];
pit = left;
}
//总循环结束,即左右下标相遇时,此时将原先保留的数据填入相遇时的坑位中
a[pit] = key;
return pit;
}
void QuickSort2(int* a, int begin, int end)//[begin,end]
{
//递归的返回条件
if (begin >= end)//当区间不存在或区间只有一个值时
{
return;
}
//单趟排序:挖坑法
int pit = PartSort2(a, begin, end);
//单趟排序完成,数组被分为三个区间
//[begin,pit-1] pit [pit+1,end]
QuickSort2(a, begin, pit - 1);
QuickSort2(a, pit + 1, end);
}
基于快排的一组选择题:
需要注意的是由于快排中有haore法、挖坑法等,二者所得到的结果不一定相同,因此会有不定项选择的情况(即多选)。
设一组初始记录关键字序列为(65,56,72,99,86,25,34,66),则以第一个关键字65为基准而得到的一趟快 速排序结果是()
A、34,56,25,65,86,99,72,66
B、25,34,56,65,99,86,72,66
C、34,56,25,65,66,99,86,72
D、34,56,25,65,99,86,72,66
③前后指针法
初始时,prev指针指向序列开头,cur指针指向prev指针的后一个位置。
然后判断cur指针指向的数据是否小于key,若小于,则prev指针后移一位,并让cur 指向的数据与prev指向的数据交换,然后cur指针自增。
当cur指针指向的数据小于key时,prev先后移一位,与cur指向的数据交换,cur再自增。当cur指针指向的数据大于key时,则cur指针自增。
当cur指针往后走到已经越界,这是我们将prev指向的内容与key进行交换。结束,此时key左边的数据比key小,key右边的数据比key大。
int PartSort3(int* a, int begin, int end)
{
int prev = begin;
int cur = begin + 1;
int key = begin;
while (cur <= end)//[begin,end]
{
if (a[cur] < a[key]&&++prev!=cur)//此处将++prev放入了if语句中,若prev=cur此时二者指向相同,交换无意义,故有++prev!=cur的写法
{
Swap(&a[prev], &a[cur]);
}
cur++;
}
//cur首次越界后
Swap(&a[prev], &a[key]);
key = prev;
return key;
}
void QuickSort3(int* a, int begin, int end)//[begin,end]
{
//递归的返回条件
if (begin >= end)//当区间不存在或区间只有一个值时
{
return;
}
//单趟排序:挖坑法
int key = PartSort3(a, begin, end);
//单趟排序完成,数组被分为三个区间
//[begin,key-1] key [key+1,end]
QuickSort3(a, begin, key - 1);
QuickSort3(a, key + 1, end);
}
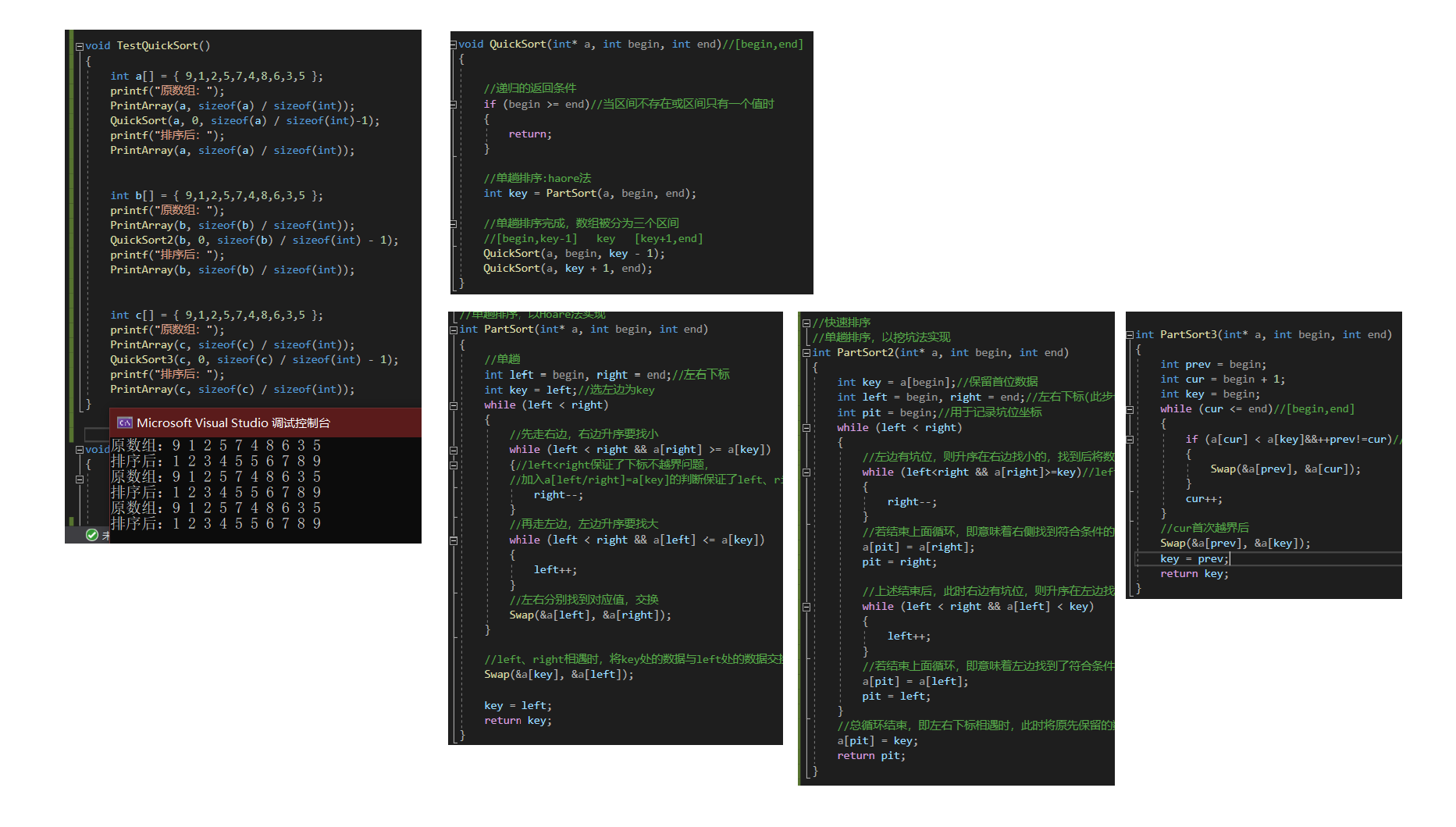
④针对key的改进
对于上述的快排方法,选择出来的基数key影响快排效率,若所选择的key接近于中位数,则效率相对较优,若所选的key为极小值或极大值时,即所给数组原先就有序或接近有序时,快排效率相对较低(当数据很多时,由于使用了递归,很容易出现栈溢出的现象)。
解决方法:
1、随机选择key
2、三数取中:第一个、中间、最后一个,选择不是最大,也不是最小的那个
int GetMinIndex(int* a, int begin, int end)//三数取中
{
int mid = (begin + end) / 2;
if (a[begin] < a[mid])//找中间值
{
if (a[mid] < a[end])
{
return mid;
}
else if (a[begin] < a[end])//a[mid] > a[end] && a[begin] < a[end]
{
return end;
}
else//a[mid] > a[end] && a[begin] > a[end]
{
return begin;
}
}
else //a[begin]>=a[mid]
{
if (a[mid] > a[end])
{
return mid;
}
else if (a[end] > a[begin])// a[mid] < a[end] && a[end] > a[begin]
{
return begin;
}
else//a[mid] < a[end] && a[end] < a[begin]
{
return end;
}
}
}
在原先的单趟排序上做出的改动:
int PartSort3(int* a, int begin, int end)
{
int prev = begin;
int cur = begin + 1;
int key = begin;
//对key取值做出的调整:三数取中法
int mid = GetMinIndex(a, begin, end);
Swap(&a[mid], &a[key]);
while (cur <= end)//[begin,end]
{
if (a[cur] < a[key]&&++prev!=cur)//此处将++prev放入了if语句中,若prev=cur此时二者指向相同,交换无意义,故有++prev!=cur的写法
{
Swap(&a[prev], &a[cur]);
}
cur++;
}
//cur首次越界后
Swap(&a[prev], &a[key]);
key = prev;
return key;
}
void QuickSort3(int* a, int begin, int end)//[begin,end]
{
//递归的返回条件
if (begin >= end)//当区间不存在或区间只有一个值时
{
return;
}
//单趟排序:挖坑法
int key = PartSort3(a, begin, end);
//单趟排序完成,数组被分为三个区间
//[begin,key-1] key [key+1,end]
QuickSort3(a, begin, key - 1);
QuickSort3(a, key + 1, end);
}
⑤小区间优化
递归划分区间,当区间比较小时,就不再用递归划分去排序这个小区间,可以考虑使用其它排序对小区间做处理。比如:直接插入排序(希尔排序针对大量数据),如此可减少很多递归次数。
该调整在QuickSort单趟排序后。
void QuickSort3(int* a, int begin, int end)//[begin,end]
{
//递归的返回条件
if (begin >= end)//当区间不存在或区间只有一个值时
{
return;
}
//单趟排序:挖坑法
int key = PartSort3(a, begin, end);
//单趟排序完成后
if (end - begin > 10)//大区间仍旧使用递归
{
//单趟排序完成,数组被分为三个区间
//[begin,key-1] key [key+1,end]
QuickSort3(a, begin, key - 1);
QuickSort3(a, key + 1, end);
}
else//小区间使用直接插入排序
{
InsertSort(a+begin, end - begin + 1);//此处快速排序区间为[begin,end],直接插入排序为[0,n),
}
}
⑥快排非递归写法
//快排的非递归法
//需要掌握非递归方法的原因:极端场景下,如果深度太深,会出现栈溢出的现象
//改法一:将递归直接该为循环:例如斐波那契额数列、归并排序
//改法二:用数据结构栈模拟递归过程
void QuickSortNonR(int* a, int begin, int end)
{
ST st;
StackInit(&st);
//先入栈,栈满足后进先出的条件,单趟排序需要一个左右区间[begin,end],则先把这段区间入栈
StackPush(&st, end);
StackPush(&st, begin);//这样出栈时就取到了[begin,end]区间
while (!StackEmpty(&st))//栈不为空时循环继续,说明还有区间没有排完
{
//取区间左端
int left = StackTop(&st);
StackPop(&st);
//取区间右端
int right = StackTop(&st);
StackPop(&st);
//单趟排序得到key值
int key = PartSort3(a, left, right);
//[left,key-1] key [key+1,right]
//根据key值划分左右区间再次进行单趟排序
//此处为了模拟递归时的先左后右(类似于前序遍历),入栈时先入key右边区间,再入key左边区间
//如此下一次出栈进行单趟排序时,能先处理左区间,再处理右区间
if (key + 1 < right)//key+1<right时,表明此时右区间中值大于一个
{
StackPush(&st, right);
StackPush(&st, key + 1);
}
if (left < key - 1)//left < key - 1时,表明此时左区间中值大于一个
{
StackPush(&st, key - 1);
StackPush(&st, left);
}
}
StackDestroy(&st);
}
此处若不适使用栈来模拟递归(处理过程类似于二叉树的前序遍历),也可以使用队列完成(处理过程类似于二叉树的层序遍历),只不过队列的特性是先进先出,入队时需要注意区间选择问题。
并归排序
1、递归法
//归并排序
//时间复杂度:O(N*logN)
//空间复杂度:O(N)归并排序需要借助数组开辟额外空间.
#include<string.h>
void _MergeSort(int* a, int begin, int end, int* tmp)
{
//参数一:原数组; 参数二、三:处理子序列需要的区间 参数四:用于并归的动态数组
if (begin >= end)
return;//当区间内只剩一个数或区间不存在时,递归停止
int mid = (begin + end) / 2;//算出划分左右子序列的中间值
//[begin,mid] [mid+1,end]
//类似后序遍历进行归并
//1、分治递归,让子区间有序
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
//2、归并,[begin,mid] [mid+1,end],对两个区间,取数放入动态区间中,若有剩余,再处理剩余区间元素
int begin1 = begin, begin2 = mid + 1;
int end1 = mid, end2 = end;
int i = begin1;//此处不能直接使i赋值为0,因为子序列是从[begin,end]开始,begin在不同的子序列中下标不同
while (begin1 <= end1 && begin2 <= end2)//当左右子序列都没有排完时
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)//处理剩余数组元素
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//将排序好的数据拷贝到原数组中
memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
void MergeSort(int* a, int n)//此处传入的区间为[0,n),n为数组元素总个数
{
//需要借助额外的数组:每次都从原数组中取数据,在动态数组中排序合并,又放回原数组中
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc:fail\n");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);//此处给的区间是[0,n-1],开区间还是闭区间看自己控制
free(tmp);
}
2、非递归法
非递归法实现并归排序不适合用借助栈,在上面的快排中,使用栈或队列不影响排序,因为对区间的处理具有独立性,而此处的并归排序中,需要先处理其左右子区间,得到有序数组才能处理本身,也是因此递归中使用的方法类似于后序遍历。
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc:fail\n");
exit(-1);
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)//2*gap:一个gap代表一组间距,并归一次需要两组,故下次从第三组开始
{
int begin1 = i, begin2 = i + gap;
int end1 = i + gap - 1, end2 = i + gap * 2 - 1;
int j = begin1;//此处不能直接使i赋值为0,因为子序列是从[begin,end]开始,begin在不同的子序列中下标不同
/* int m = end2 - begin1 + 1;*/
//越界-边界修正(适用于同组gap整体拷贝的情况)
if (end1 >= n)
{
end1 = n - 1;
//[begin2,end2]修正为不存在区间[n,n-1]
begin2 = n;
end2 = n - 1;
}
else if (begin2 >= n)
{
begin2 = n;
end2 = n - 1;
}
else if (end2 >= n)
{
end2 = n - 1;
}
适用于单独一组拷贝的情况:若是end1越界或bigne2越界,则可以直接不归并:
//if (end1 >= n || begin2 >= n)
//{
// break;
//}
//else if (end2 >= n)//需要修正边界
//{
// end2 = n - 1;
//}
while (begin1 <= end1 && begin2 <= end2)//当左右子序列都没有排完时
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)//处理剩余数组元素
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
单独一组拷贝:只需对最后越界时进行修正
//memcpy(a+i, tmp+i, m* sizeof(int));
单组归并在begin1~end2之间,但begin1后续参与了操作非原始值,此处用i替代,2*gap表示归并的元素个数
}
//同组gap整体拷贝:将排序好的数据拷贝到原数组中
memcpy(a, tmp, n * sizeof(int));
gap *= 2;
}
free(tmp);
}
计数排序
//时间复杂度O(max(range,N))
//空间复杂度O(range)
void CountSort(int* a, int n)
{
//计算数组最大最小值
int min = a[0], max = a[0];
for (int i = 1; i < n; i++)
{
if (a[i] < min)
min = a[i];
if (a[i] > max)
max = a[i];
}
//统计次数的数组
int range = max - min + 1;//需要开辟一个能装下最大数与最小数元素差的数组,[min,max]之间的数据在数组中按顺序各占一个元素位置
int* count = (int*)malloc(sizeof(int) * range);
if (count == NULL)
{
printf("malloc:fail\n");
exit(-1);
}
memset(count, 0, sizeof(int) * range);
//统计次数
for (int i = 0; i < n; i++)//将原数组元素中出现的值做统计
{
count[a[i] - min]++;//-min是相对映射,使原数组值在统计数组中从0开始,也能解决负数问题
}
//回写排序
int j = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)//统计数组中该值出现几次,在原数组中映射元素就写入几次
{
a[j++] = i + min;//+min为映射回去
}
}
}
边栏推荐
- 自媒体创作怎样提高原创度,打造爆款作品?
- "Second Uncle" is popular, do you know the basic elements of "exploding" short videos from the media?
- Wireless vibrating wire acquisition instrument remote modification method
- 【typescript】使用antd中RangePicker组件实现时间限制 当前时间的前一年(365天)
- 分享一个Chrome控制台数据获取的例子
- Enterprise Network Planning Based on Huawei eNSP
- Closures in JS
- 【622. 设计循环队列】
- SQL函数 TRUNCATE
- 为什么IDEA连接mysql Unable to resolve table 编译报错但是可以运行
猜你喜欢
![PHP+MYSQL [Student Information Management System] (Minimalist Edition)](/img/86/d5d39eef0600acabbf3ac16c255c18.png)
PHP+MYSQL [Student Information Management System] (Minimalist Edition)
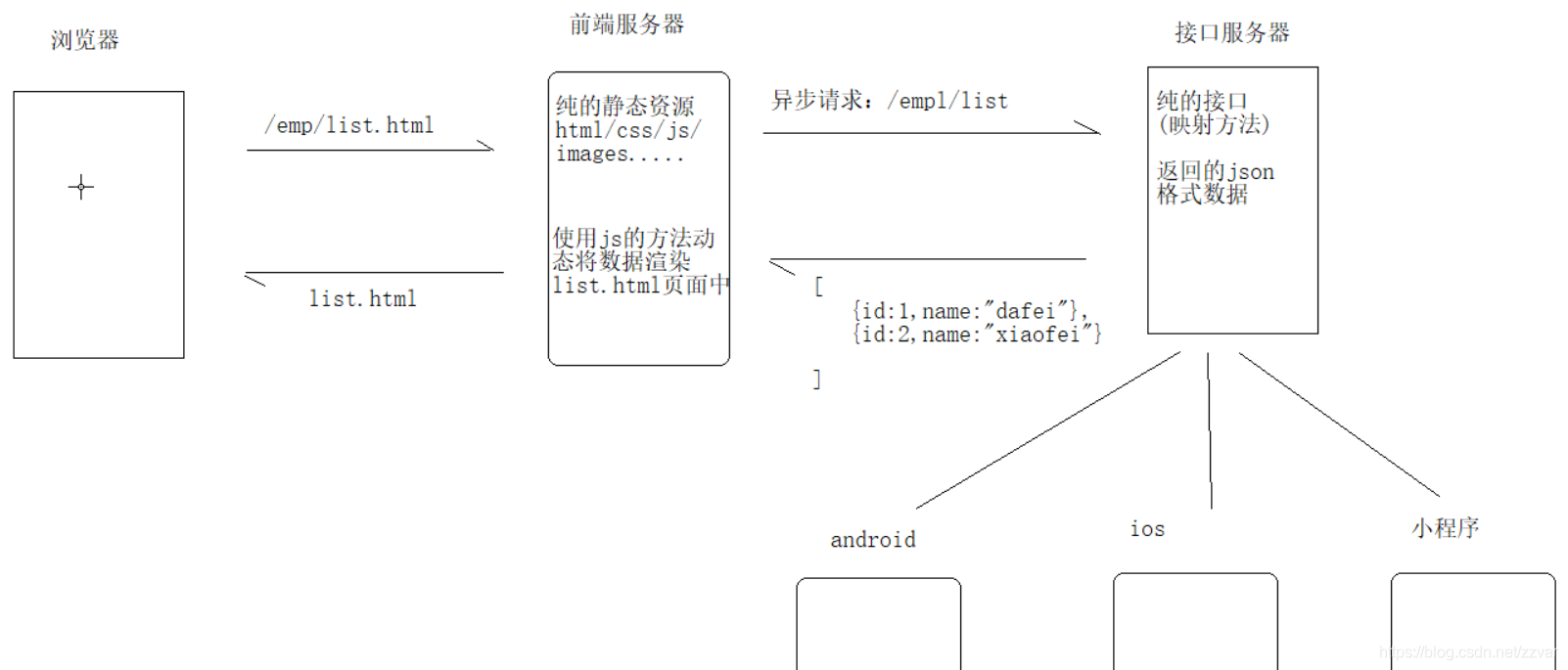
RESTful 风格(详细介绍 + 案例实现)
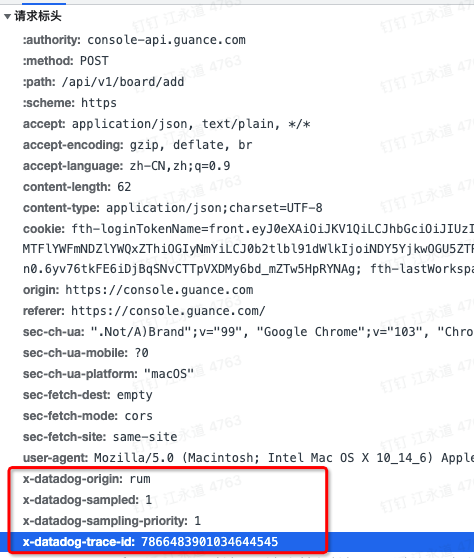
分享一个Chrome控制台数据获取的例子

This binding to detailed answers
Win11怎么修改关机界面颜色?Win11修改关机界面颜色的方法
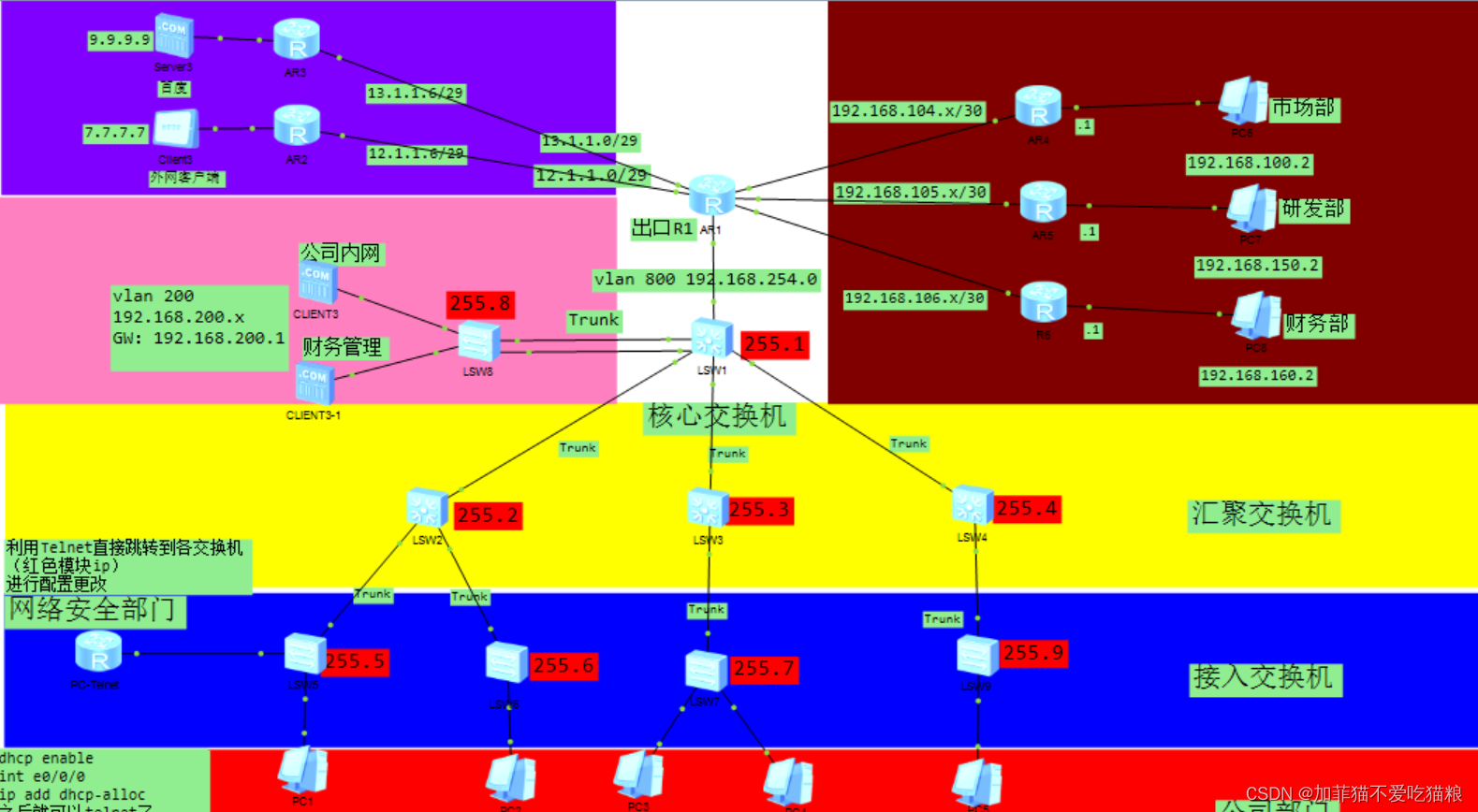
基于华为eNSP的企业网络规划
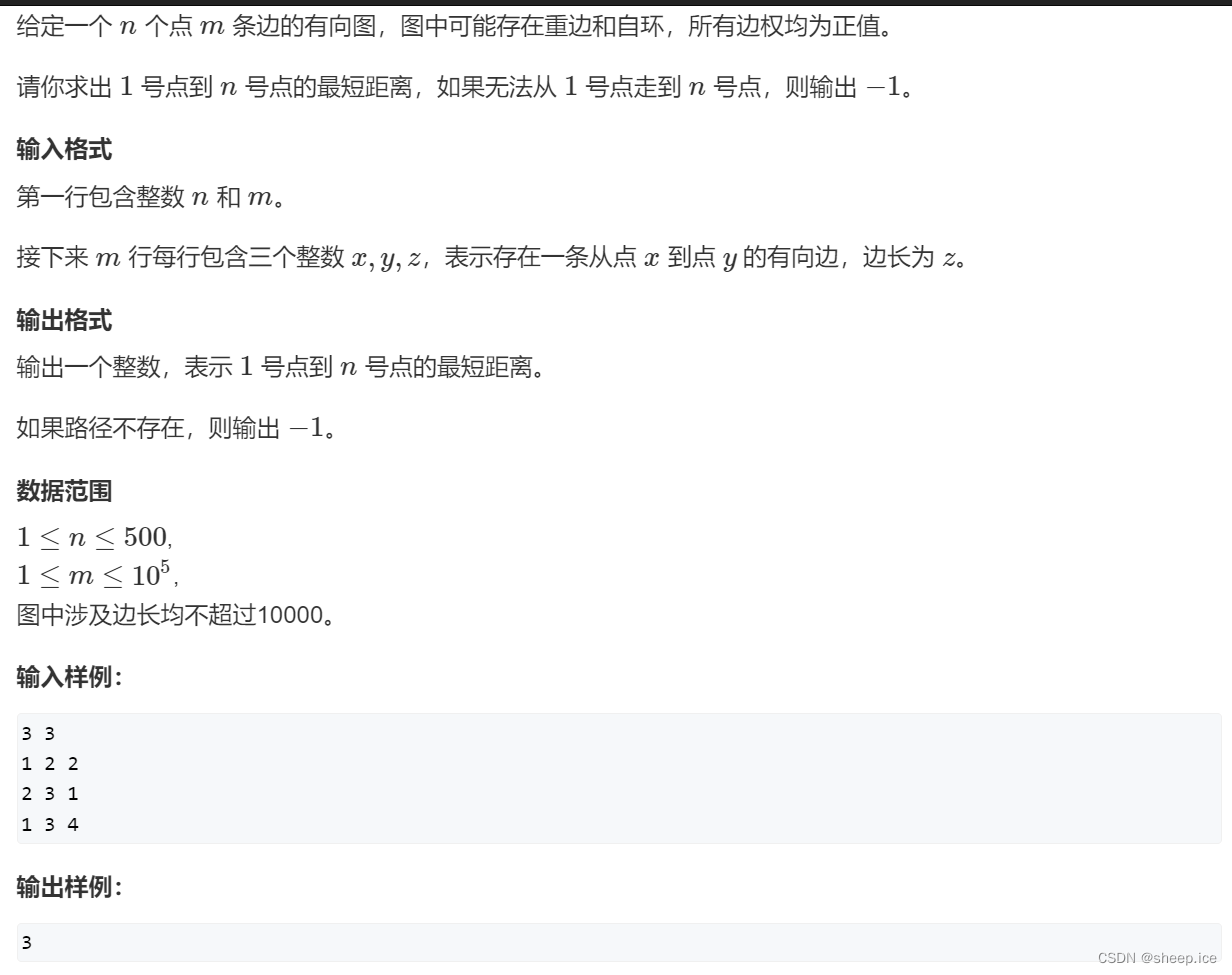
Do you know Dijkstra of graph theory?
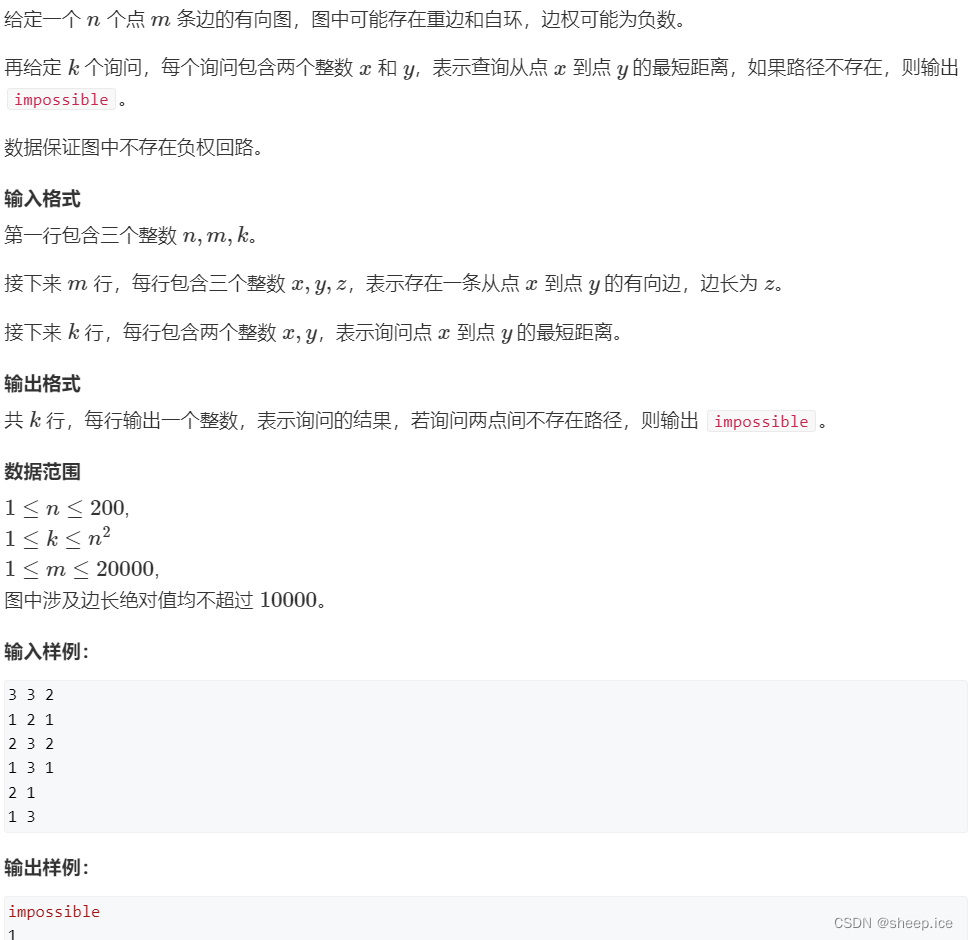
图论之Floyd,多源图最短路如何暴力美学?
How to improve the originality of self-media creation and create popular works?
【C语言】函数哪些事儿,你真的get到了吗?(2)
随机推荐
Redis all
【C语言】虐打循环结构练习题
selenium chrome driver运行时的cannot determine loading status from target frame detached问题
80篇国产数据库实操文档汇总(含TiDB、达梦、openGauss等)
Mysql 基本操作指南之mysql查询语句
动态组件-component
UAC绕过学习-总结
RISC-V instruction format and 6 basic integer instructions
static修饰的函数有什么特点(static可以修饰所有的变量吗)
Get out of the machine learning world forever!
Oracle update误操作单表回滚
好用的php空间,推荐国内三个优质的免费PHP空间[通俗易懂]
ttl电平与rs232电平转换电路(232电平定义)
C语言结构体(入门)
目前想通过提取本地excel文件创建数据表,在sql语句这出了一些问题
scrapy框架初识1
Reading IDEO, Design Changes Everything
我的创作纪念日
“多源异构”和“异构同源”定义区分详解「建议收藏」
你知道图论的Dijkstra吗?