当前位置:网站首页>Knapsack Problem - Dynamic Programming - Theory
Knapsack Problem - Dynamic Programming - Theory
2022-08-02 15:33:00 【Old stubborn and cute】
01背包
现在有n个物品,Each item up to take a, 有一个背包,It on the outside weight cannot be more than the sum ofW,第iThe weight of the goods it iswi,价值是vi, 现在的问题是,In not more than under the limit of volume,Most can obtain what is the sum of the value of the goods.
(1<=n<= 2000, 0<= W<= 2000, vi>0, wi> 0)
解决方案1
Let's first consider iterate through all the way,If the item number isn,那么总的方案数就是2 ^ n种(选或者不选),我们可以用dfs搜索实现.
//Recursive solution code,Need to use memory, search
int dfs(int i, int j)
{
if(i==0||j<0) return 0;
if(dp[i][j]!=-1) return dp[i][j];
dp[i][j]= dfs(i-1,j);
if(j>=w[j])dp[i][j]=max(dp[i][j],dfs(i-1,j-w[i]));
return dp[i][i];
}
/*初始化dp数组为-1, answer=dfs(n, W). Attempt to solve the recursive dynamic programming were compared with search.*/
但是nThe biggest can reach2000,显然2 ^ 2000The complexity of the hard to accept,Can we get a smaller time complexity method?
解决方案2
我们考虑用dp[i][j]表示已经处理了前i个物品,Now things in the backpack weight not greater than the sum ofjCan obtain the biggest value under the condition of the sum of.
状态转移方程:
dp[i][j] = max(dp[i-1][j], dp[i- 1][j-wi]+vi)
dp[i-1][ij]:表示不选第i个物品.
dp[i- 1][j-wi]+vi:表示选第i个物品.
//递推解决
for(int i=0;i<=W;i++) dp[0][i]=0;
for(int i=1;i<=n;i++)
for(int j=0;j<=W;j++)
{
d[i][j]= dp[i-1][j];
if(j>=w[i])
dp[i][j]=max(dp[i][j],dp[i-1][j-w[i]]+v[j]);
}
//answer=dp[n][W]
空间优化
使用滚动数组: cur表示当前层,last表示上一层
for(int j=0;j<=W;j++)cur[j]=0;
for(int i=1;i<=n;j++)
{
for(int j=0;j<=W;j++)
last[j]=cur[j],cur[j]=0;
for(int j=0;j<=W;j++)
{
cur[j]=last[j];
if(j>=w[i])
cur[j]=max(cur[j],last[j-w[i]);
}
}
// answer = cur[W]
无限背包
现在有n个物品,Each item can take any number of times,有一个背包,It on the outside weight cannot be more than the sum ofW,第iThe weight of the goods it iswi,价值是vi, 现在的问题是,In not more than under the limit of volume,Most can obtain what is the sum of the value of the goods.
(1<=n<= 2000, 0<= W<= 2000, vi>0, wi> 0)
解决方案1
To convert the infinite knapsack problem01背包问题,第i种物品最多有W / wiA work,Put each item into the most likely to buy the number of,然后用01背包解决问题.最坏复杂度O(W* W * n).
解决方案2
我们考虑用dp[i][j]表示已经处理了前i种物品,Now things in the backpack weight not greater than the sum ofjCan obtain the biggest value under the condition of the sum of.
状态转移方程:
dp[i][j]= max(dp[i-1[j], dp[i][j-wi]+vi)
dp[i-1][j]:表示不选第i种物品.
dp[i][j-wi]+vi :Said to choose ai种物品.
memset(dp,0,sizeof(dp));
for(int i=1;i<=n;i++)
for(int j=w[i];j<=W;j++)
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
//answer=dp[W]
多重背包
现在有n个物品,Each item can takeci次,有一个背包,It on the outside weight cannot be more than the sum ofW,第iThe weight of the goods it iswi,价值是vi, 现在的问题是,In not more than under the limit of volume,Most can obtain what is the sum of the value of the goods.
(1 <=n<= 2000, 0<= W<= 2000, vi>0, wi> 0)
解决方案1
把第i种物品拆成ci个,然后直接01Backpack for the answer.
复杂度O(n * ci *W)
解决方案2
Using binary split:
Took up tociOther items into:1,2,4,8, 16… 2^n , k .
其中n是最大的满足1 +2 +4 +8 +16+ … + 2^n <= ci 的数.
k =ci -1 -2 -4 -8 -16 -… -2 ^n.
例子:
对于ci==7的物品,We for this kind of items, there are8种决策,Respectively is a choice0, 1, 2, 3, 4, 5, 6, 7个.法1:拆成7个数量为1的物品(0000000-1111111)进行01A backpack can get it8种决策. 法2:如果把7Into the number of1个,2个,4The three items(000-111),With these three items01Backpack can also cover the above8种决策.
对于ci==12的物品,Into the number of1个,2个,4个,4个的物品(0000-1111),Using these four items01背包(12<16)能覆盖0-12这13种决策.
memset(dp,0,sizeof(dp));
for(int i=1;i<=n;i++)
{
int num;
for(num=1;num<=c[i];num*=2)
{
int cw=num*w[i];
int cv=num*v[i];
for(int j=W;j>=cw;j--)
dp[j]=max(dp[j], dp[j-cw]+cv);
c[i]-=num;
}
num=c[i];
if(num)
{
int cw=num*w[i];
int cv=num*v[i];
for(int j=W;j>=cw;j--)
dp[j]=max(dp[j],dp[j-cw]+cv);
}
}
状态压缩dp
概念
We have more than one item,Each item has a state,We use a number to indicate the status of every item,This is the state of compression.In a nutshell is the state of multiple items into a digital.
举例
我们有4个物品,Each item has two states are respectively with and without,我们用0表示没有,用1表示有.
| 高~>低 | Some of the items | 没Some of the items |
|---|---|---|
| 1010 | 1, 3 | 0, 2 |
| 0110 | 1, 2 | 0, 3 |
| 1011 | 0, 1, 3 | 2 |
| For a compressed after decimal numberS通过**(S>>i)& 1**获取到第i个物品的信息. |
例如:S=10=1010 (二进制),想获取第1个物品的信息,(S>>1)=5=0101 (二进制),At its lowest level is an item of information,所以(S>> 1) & 1Get the first item of information.
简单例题
有n个城市,标号从0到n- 1,Know now that the distance between each two cities,第i个城市和第jThe distance between the cities asd [i][j],Now there was a man want from0Cities began to put all the number how many distance at least go again need to go.
(1 <=n<= 20, d[i][j]> 0)
解题思路
枚举所有的方案,只需要枚举1到n-1The whole arrangement can,For each scheme distance calculation again.时间复杂度O( (n- 1)! )
深入思考:Same for all through the city,最后-A city to the same situation,We just need to keep the smallest distance that is ok.
如果一共有5个城市,分别是0, 1, 2, 3, 4考虑这两种情况
| 0->1->3->2 | 距离=10 | (1) This path does not need to extend the |
|---|---|---|
| 0->3->1->2 | 距离= 9 | (2) |
dp[i][mask] : After the situation of the city ismask,最后停在i的最短距离
状态转移方程: dp[i][S] = max(dp[j][S^(1<<i)) 满足(S>>j& 1)== 1 &&j!= i
复杂度0 (n* (2 ^(n-1)))
for(int mask=0;mask<(1<<n);mask++)
for(int i=0;i<n;i++)
dp[j][mask]=inf;
dp[0][1]=0;
for(int mask=0;mask<(1<<n);mask++)
for(int i=0;i<n;i++)
if(mask>>i&1)
for(int j=0;j<n;j++)
if(j!=i&&mask>>j&1)
dp[i][mask]=min(dp[i][mask],dp[j][mask^(1<<i)]);
边栏推荐
- DP1332E内置c8051的mcu内核NFC刷卡芯片国产兼容NXP
- Publish module to NPM should be how to operate?Solutions to problems and mistake
- Open the door of power and electricity "Circuit" (2): Power Calculation and Judgment
- Win11怎么在右键菜单添加一键关机选项
- 质数相关问题-小记
- 用U盘怎么重装Win7系统?如何使用u盘重装系统win7?
- Win10无法连接打印机怎么办?不能使用打印机的解决方法
- Win10 cannot directly use photo viewer to open the picture
- Do Windows 10 computers need antivirus software installed?
- Detailed explanation of MATLAB drawing function plot
猜你喜欢

3. User upload avatar
为vscode配置clangd
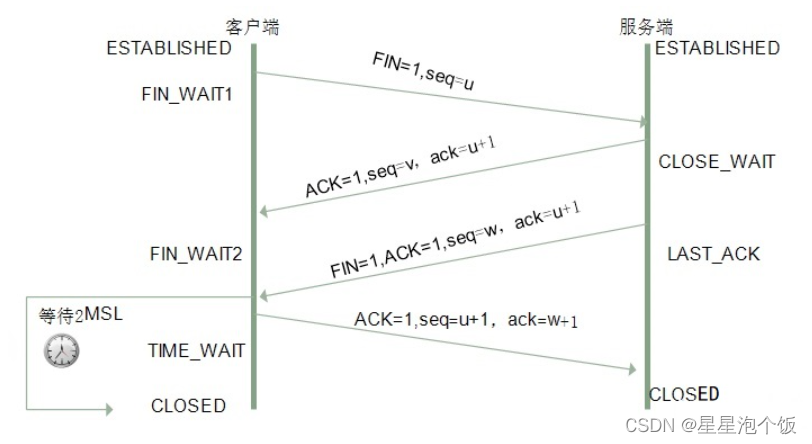
TCP三次握手、四次挥手
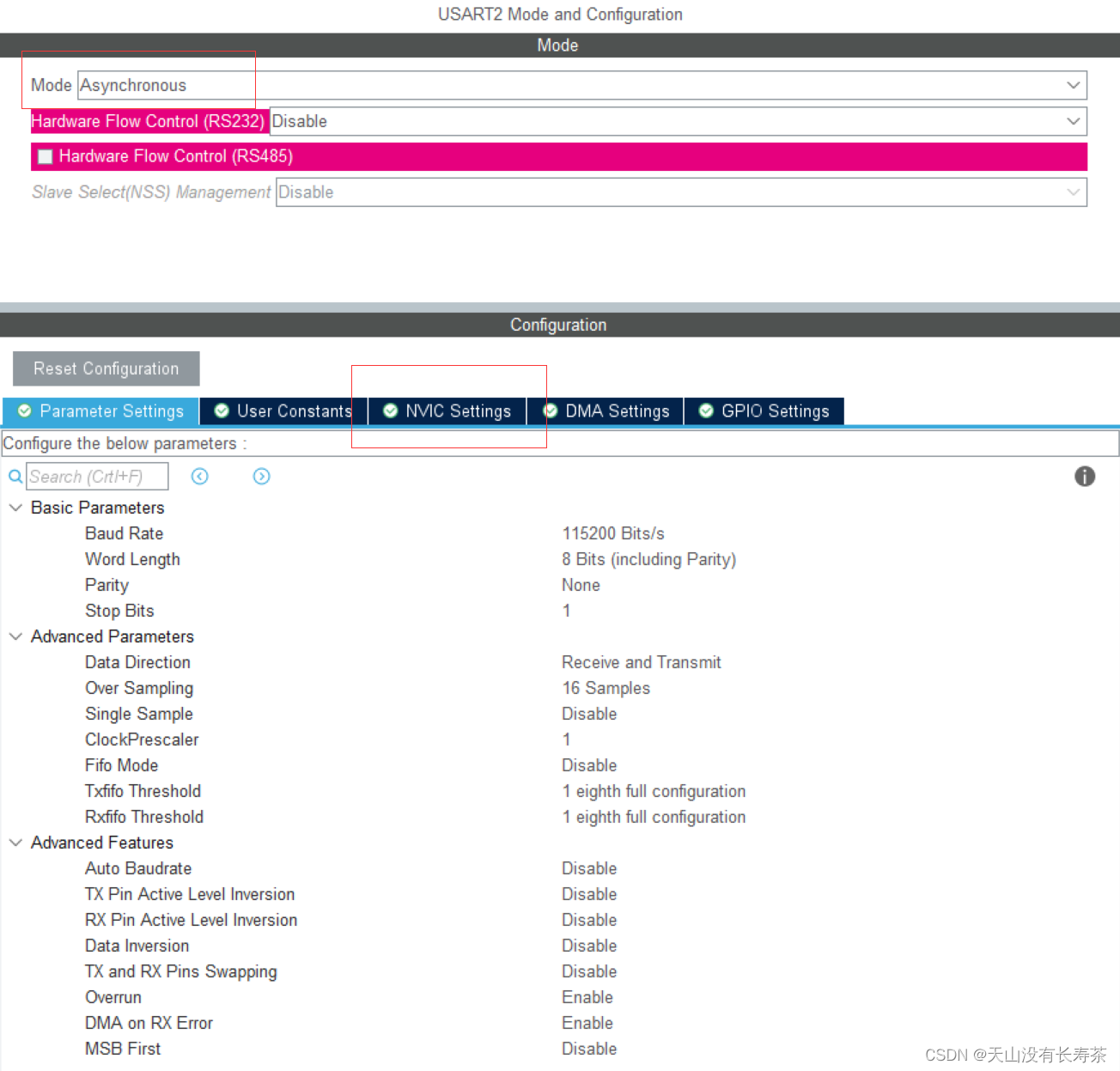
STM32LL library - USART interrupt to receive variable length information
What should I do if Windows 10 cannot connect to the printer?Solutions for not using the printer

win10 system update error code 0x80244022 how to do
推开机电的大门《电路》(二):功率计算与判断
倍增和稀疏表

Win11系统找不到dll文件怎么修复
软件测试基础知识(背)
随机推荐
Daily - Notes
发布模块到npm应该怎么操作?及错误问题解决方案
pytorch模型转libtorch和onnx格式的通用代码
Mysql lock
软件测试基础知识(背)
Redis常见面试题
3. User upload avatar
基于矩阵计算的线性回归分析方程中系数的估计
日常-笔记
Redis的线程模型
Configure clangd for vscode
win11一直弹出用户账户控制怎么解决
CI24R1小模块2.4G收发模块无线通信低成本兼容si24r1/XN297超低功耗
Win7遇到错误无法正常开机进桌面怎么解决?
13.56MHZ刷卡芯片CI521兼容cv520/ci520支持A卡B卡MIFARE协议
MATLAB绘制平面填充图入门详解
一篇文章彻底理解Redis的持久化:RDB、AOF
How to simulate 1/3 probability with coins, and arbitrary probability?
General syntax and usage instructions of SQL (picture and text)
What should I do if I install a solid-state drive in Win10 and still have obvious lags?