当前位置:网站首页>倍增和稀疏表
倍增和稀疏表
2022-08-02 14:10:00 【老顽固也可爱】
倍增、ST、RMQ
1、倍增
任意整数均可被表示成若干个2的次幂项之和。例如:
整数5,其二进制表示为101,该二进制数从右向左第0、2位均为1,则5=2+20
整数26,其二进制表示为11010,该二进制数从右向左第1、3、4位均为1,则 26 = 2 4 + 2 3 + 2 1 26=2^4+2^3+2^1 26=24+23+21 。也就是说,2的次幂项可被拼成任一需要的值。
倍增,顾名思义就是成倍增加。若问题的状态空间特别大,则一步步递推的算法复杂度太高,可以通过倍增思想,只考察2的整数次幂位置,快速缩小求解范围,直到找到解。
2、ST
ST(Sparse Table,稀疏表)算法采用了倍增思想,在 O ( n l o g n ) O(nlogn) O(nlogn) 时间构造一个二维表之后,可以在 O ( 1 ) O(1) O(1) 时间在线查询 [ l , r ] [l, r] [l,r] 区间的最值,有效解决 在线RMQ(Range Minimum/Maximum Query,区间最值查询)问题。如何实现呢?
设 F [ i , j ] F[i,j] F[i,j] 表示 [ i , i + 2 j − 1 ] [i, i+2^j-1] [i,i+2j−1] 区间的最值,区间长度为 2 j 2^j 2j。
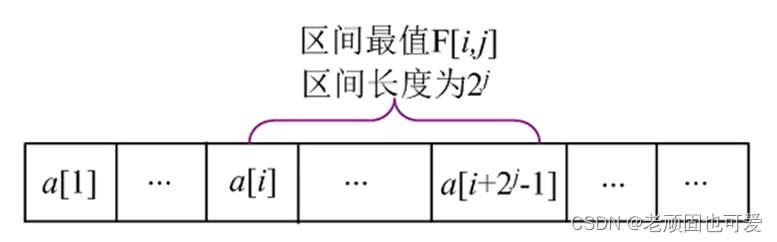
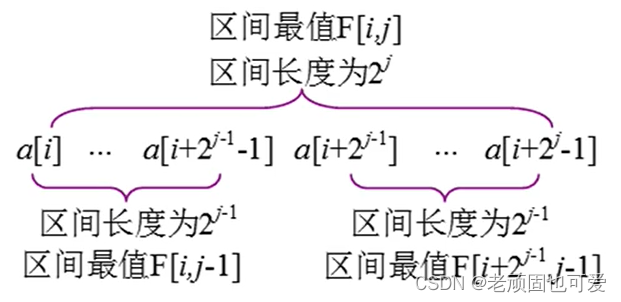
根据倍增思想,长度为 2 j 2^j 2j 的区间可被分成两个长度为 2 j − 1 2^{j-1} 2j−1 的子区间,然后求两个子区间的最值即可。
递推公式: F [ i , j ] = m a x ( F [ i , j − 1 ] , F [ i + 2 j − 1 , j − 1 ] ) F[i,j]=max(F[i,j-1], F[i+2^{j-1},j-1]) F[i,j]=max(F[i,j−1],F[i+2j−1,j−1])
2.1 ST表的创建
若 F [ i , j ] F[i, j] F[i,j] 表示 [ i , i + 2 j − 1 ] [i, i+2^{j}-1] [i,i+2j−1] 区间的最值,区间长度为 2 j 2^j 2j,则和 j j j 的取值范围是多少呢?
若数组的长度为 n n n ,最大区间长度 2 k ≤ n < 2 k + 1 2^k≤n<2^{k+1} 2k≤n<2k+1,则 k = ⌊ l o g 2 n ⌋ k=\lfloor log_2n\rfloor k=⌊log2n⌋, 比如:
- n=8时k=3,
- n=10时k=3。
在程序中,k=log2(n), 也可用通用表达方式 k=log(n)/log(2),log()表 示以 e为底的自然对数。
void ST_create() {
for(int i=1; i<=n; i++) {
F[i][0]=a[i];// 区间[i,i]的最值,区间长度位2^0
}
int k=log(n)/log(2.0);
for(int j=1; j<=k; j++) {
for(int i=1; i<=n-(1<<y)+1; i++) {
F[i][j]=max(F[i][j-1],F[i+(1<<j-1)][j-1])
}
}
}
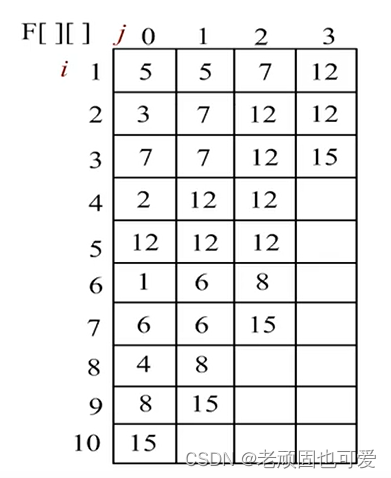
例如,有10个元素 a [ 1..10 ] = 5 , 3 , 7 , 2 , 12 , 1 , 6 , 4 , 8 , 15 a[1..10]={5,3,7,2,12,1,6,4, 8,15} a[1..10]=5,3,7,2,12,1,6,4,8,15,创建查询最大值的ST表。 F [ i , j ] F[i,j] F[i,j] 表示 [ i , i + 2 j − 1 ] [i, i+2^j-1] [i,i+2j−1] 区间的最值,区间长度为2。
2.2 ST表查询
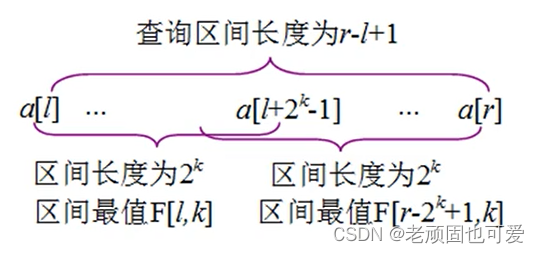
若查询 [ l , r ] [l,r] [l,r] 区间的最值,则首先计算 k k k 值,和前面的计算方法相同,区间长度为 r − l + 1 r-l+1 r−l+1, 2 k ≤ r − l + 1 < 2 k + 1 2^k\leq r-l+1<2^{k+1} 2k≤r−l+1<2k+1, 因此 $k=log2(r-l+1) $。
若查询区间的长度大于或等于 2 2 2 且小于 2 k + 1 2^{k+1} 2k+1 ,则根据倍增思想,可以将查询区间分为两个查询区间,取两个区间的最值即可。两个区间分别为从向后的 2 k 2^k 2k 个数及从 r r r 向前的 2 k 2^k 2k 个数,这两个区间可能有重叠,但对求最值没有影响。
int ST_query(int l, int r){
int k=log2(r-l+1);
return max(F[l][k], F[r-(1<<k)+1][k])
}
3、RMQ
RMQ(区间最值查询)问题有多种解决方法,用线段树和ST解决RMQ问题的对比如下:
- 线段树预处理的时间为 O ( n l o g n ) O(nlogn) O(nlogn),查询的时间为 O ( l o g n ) O(logn) O(logn) ,支持在线修改
- ST预处理的时间为 O ( n l o g n ) O(nlogn) O(nlogn),查询的时间为 0 ( 1 ) 0(1) 0(1) ,不支持在线修改。
边栏推荐
- win10任务栏不合并图标如何设置
- TypeScript 快速进阶
- Win10系统设置application identity自动提示拒绝访问怎么办
- FP7126降压恒流65536级高辉无频闪调光共阳极舞台灯RGB驱动方案
- The SSE instructions into ARM NEON
- 镜像法求解接地导体空腔电势分布问题
- Win11 system cannot find dll file how to fix
- Please make sure you have the correct access rights and the repository exists.问题解决
- golang之GMP调度模型
- DP1332E内置c8051的mcu内核NFC刷卡芯片国产兼容NXP
猜你喜欢

In-depth understanding of Golang's Map

win10 system update error code 0x80244022 how to do

为android系统添加产品的过程
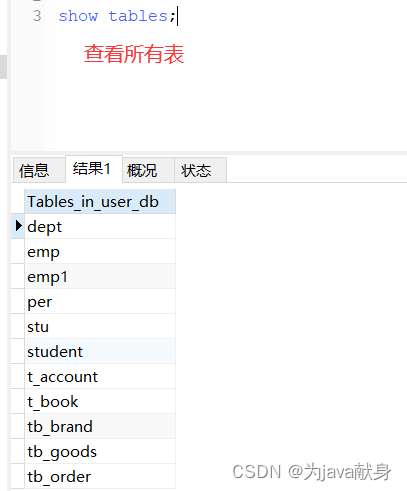
General syntax and usage instructions of SQL (picture and text)
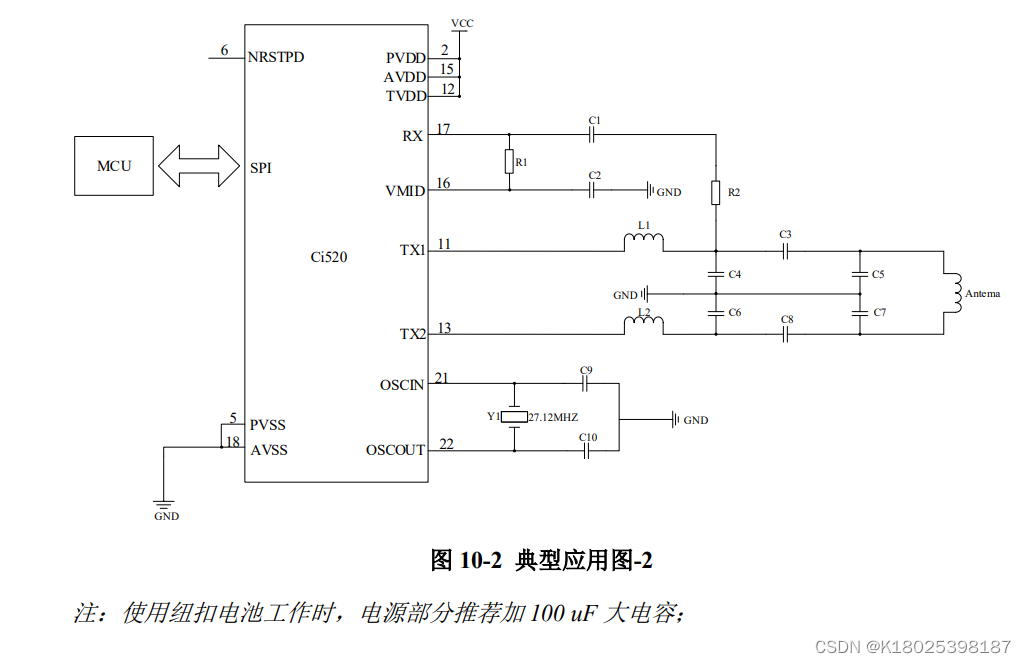
刷卡芯片CI520可直接PIN对PIN替换CV520支持SPI通讯接口

Win10 computer can't read U disk?Don't recognize U disk how to solve?
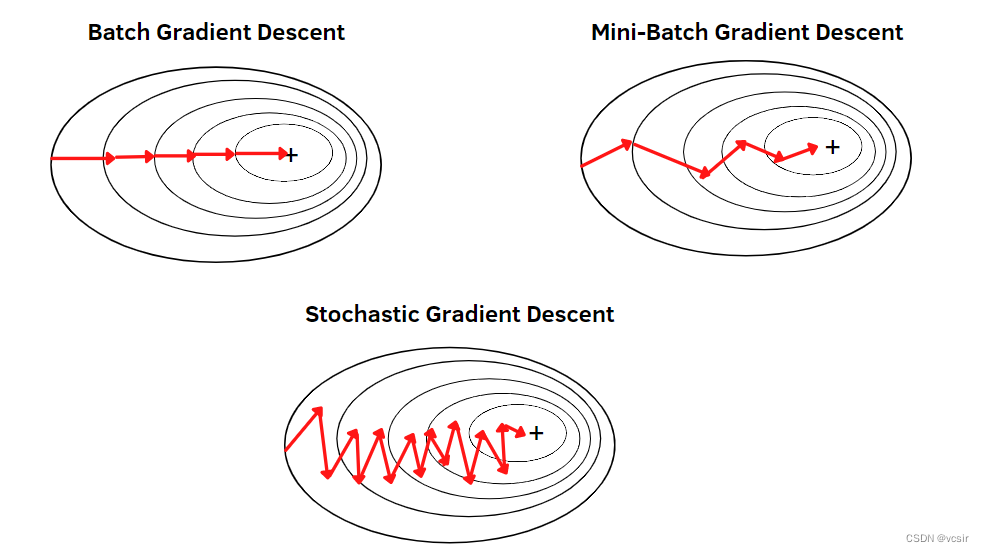
机器学习和深度学习中的梯度下降及其类型

source /build/envsetup.sh和lunch)
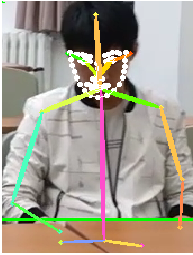
轻量化AlphaPose
蓝牙温度检测系统(基于BT08-B蓝牙模块)
随机推荐
Actual combat Meituan Nuxt +Vue family bucket, server-side rendering, mailbox verification, passport authentication service, map API reference, mongodb, redis and other technical points
FP5139电池与适配器供电DC-DC隔离升降压电路反激电路电荷泵电路原理图
Failed to install using npx -p @storybook/cli sb init, build a dedicated storybook by hand
Win10上帝模式干嘛的?Win10怎么开启上帝模式?
将SSE指令转换为ARM NEON指令
pygame绘制弧线
基于51单片机和物联网的智能家居系统(ESP8266物联网模块)
win11一直弹出用户账户控制怎么解决
Win11 system cannot find dll file how to fix
二叉树遍历之后序遍历(非递归、递归)入门详解
推开机电的大门《电路》(三):说说不一样的电阻与电导
用U盘怎么重装Win7系统?如何使用u盘重装系统win7?
ARMv8虚拟化
Publish module to NPM should be how to operate?Solutions to problems and mistake
arm push/pop/b/bl汇编指令
Win11怎么在右键菜单添加一键关机选项
Win10 computer can't read U disk?Don't recognize U disk how to solve?
win10无法直接用照片查看器打开图片怎么办
蓝牙温度检测系统(基于BT08-B蓝牙模块)
C语言函数参数传递模式入门详解