Leetcode-11: container with the most water

Answer key

　　 This is a classic question , Is it difficult? ?, It's easy to think of it .

        The exact solution to the problem is Double pointer + greedy The strategy of , Put a pointer at the beginning and the end , Each time the pointer points to a smaller number and moves inward , Record in the process of moving Max that will do .

        Why can we guarantee the optimal solution ？

        The correctness of the algorithm is verified by diagram ：

 

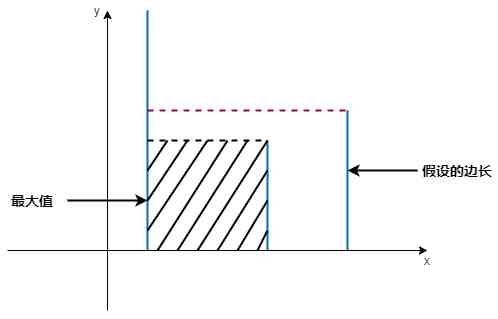
        Here we use the method of proof to the contrary , Let's first show the maximum area of the area , And then we assume a side length , if L( Right ) > L( Left ), Then the maximum area must be greater than the maximum area we have shown , But it's obviously not true , So we have to satisfy L( Right ) < L( Left ), At this point, the right pointer will move to the left to find a higher height than before .

        The time complexity of the algorithm can be controlled in $O(n)$ within .

class Solution {
    typedef long long LL;
public:
    int maxArea(vector<int>& height) {
        //  Double pointer algorithm 
        int l = 0, r = height.size() - 1;
        LL maxx = 0;
        while (l < r) {
            maxx = max(maxx, (LL) (r - l) * min(height[l], height[r]));
            //  recorded 
            int height1 = height[l];
            int height2 = height[r];
            if (height1 < height2)  {
                ++l;
                while (l < r && height1 >= height[l]) ++l;
            }
            else {
                --r;
                while (l < r && height2 >= height[r]) --r;
            }
        }
        return maxx;
    }
};