当前位置:网站首页>C++邻接矩阵
C++邻接矩阵
2020-11-08 23:48:00 【WHICH工作室】

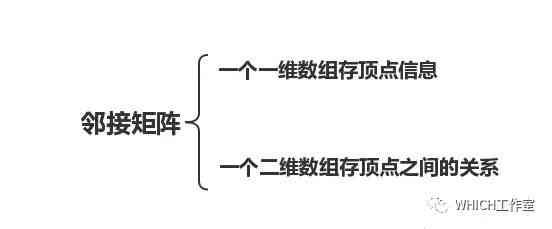
无向图和有向图在邻接矩阵中的表示方法:
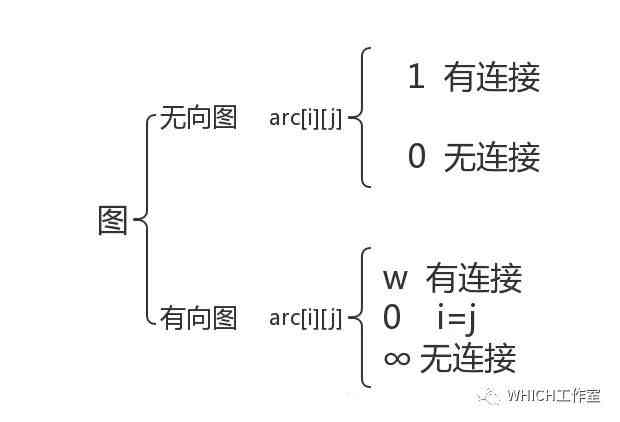
无向图和有向图大同小异,在这里只以无向图为例,代码部分通过简单调整即可对应编译有向图
邻接矩阵数据类型定义
typedef struct{ //包含权的邻接矩阵的的定义 int Vertices[MaxVertices]; //顶点信息的数组 int Edge[MaxVertices][MaxVertices]; //边信息的数组 int n,e; //总顶点数,边数}AMGraph;以如关系图为例

根据上图,我们可以写出对应的邻接矩阵:
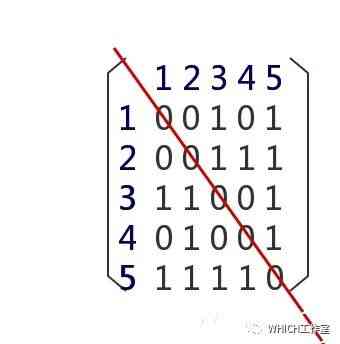
通过这个图可以看出,无向图对角线划分出来的两部分是互相对称的,由此即可通过创建无向图的邻接矩阵:
void CreateUDN(AMGraph &G) //图的生成函数{ int i,j,n1,e1,vi,vj,w; printf("请输入邻接矩阵的顶点数和边数:\n"); scanf("%d %d",&G.n,&G.e); //输入总顶点数,总边数 n1 = G.n; e1 = G.e; printf("请输入每个顶点的信息:\n"); for(i=0; i<n1; i++) //将顶点存入数组中 { scanf("%d",&G.vexs[i]); //依次输入点的信息 } for(i=0; i<n1; i++) //图的初始化 { for(j=0; j<n1; j++) { if(i=j) { G.arcs[i][j] = 0; //顶点到自身的路径为0 } else { G.arcs[i][j] = MaxWeight; //除顶点到自身外,其余均设为极大值 } } } printf("\n"); //输入顶点从0开始// for(i=0; i<e1; i++)// {// printf("请输入边的信息:\n");// scanf("%d %d %d",&vi,&vj,&w);// G.arcs[vi][vj] = w; //因为无向图是对称的,a[i][j] = a[j][i]// G.arcs[vj][vi] = w;// } //输入顶点从1开始 for(i=0; i<e1; i++) { printf("请输入边的信息:\n"); scanf("%d %d %d",&vi,&vj,&w); G.arcs[vi-1][vj-1] = w; // ① //因为无向图是对称的,a[i][j] = a[j][i] G.arcs[vj-1][vi-1] = w; // ② //无向图具有对称性的规律,通过①②实现 //有向图不具备此性质,所以只需要① }}创建完无向图对应的邻接矩阵,我们需要对输出的格式进行一下控制,使其尽量按照普通手写的方式输出
void PrintfGraph(AMGraph G) //输出邻接矩阵的信息{ int i,j; printf("输出顶点的信息为:\n"); for(i=0; i<G.n; i++) { printf("%d\t",G.vexs[i]); } printf("\n邻接矩阵为:\n"); for(i=0; i<G.n; i++) { printf("\t%d",G.vexs[i]); } for(i=0; i<G.n; i++) { printf("\n%d\t",G.vexs[i]); for(j=0; j<G.n; j++) { if(G.arcs[i][j] == MaxWeight) //两点之间无连接时权值为默认的32767,但输出时为了方便输出 "∞" { printf("%s\t","∞"); } else printf("%d\t",G.arcs[i][j]); } }}完整程序如下:
typedef int VerType;typedef int ArcType;typedef struct{ VerType vexs[MaxVertices]; ArcType arcs[MaxVertices][MaxVertices]; int n,e;} AMGraph;void CreateUDN(AMGraph &G) //图的生成函数{ int i,j,n1,e1,vi,vj,w; printf("请输入邻接矩阵的顶点数和边数:\n"); scanf("%d %d",&G.n,&G.e); //输入总顶点数,总边数 n1 = G.n; e1 = G.e; printf("请输入每个顶点的信息:\n"); for(i=0; i<n1; i++) //将顶点存入数组中 { scanf("%d",&G.vexs[i]); //依次输入点的信息 } for(i=0; i<n1; i++) //图的初始化 { for(j=0; j<n1; j++) { if(i=j) { G.arcs[i][j] = 0; //顶点到自身的路径为0 } else { G.arcs[i][j] = MaxWeight; //除顶点到自身外,其余均设为极大值 } } } printf("\n"); //输入顶点从0开始// for(i=0; i<e1; i++)// {// printf("请输入边的信息:\n");// scanf("%d %d %d",&vi,&vj,&w);// G.arcs[vi][vj] = w; //因为无向图是对称的,a[i][j] = a[j][i]// G.arcs[vj][vi] = w;// } //输入顶点从1开始 for(i=0; i<e1; i++) { printf("请输入边的信息:\n"); scanf("%d %d %d",&vi,&vj,&w); G.arcs[vi-1][vj-1] = w; // ① //因为无向图是对称的,a[i][j] = a[j][i] G.arcs[vj-1][vi-1] = w; // ② //无向图具有对称性的规律,通过①②实现 //有向图不具备此性质,所以只需要① }}void PrintfGraph(AMGraph G) //输出邻接矩阵的信息{ int i,j; printf("输出顶点的信息为:\n"); for(i=0; i<G.n; i++) { printf("%d\t",G.vexs[i]); } printf("\n邻接矩阵为:\n"); for(i=0; i<G.n; i++) { printf("\t%d",G.vexs[i]); } for(i=0; i<G.n; i++) { printf("\n%d\t",G.vexs[i]); for(j=0; j<G.n; j++) { if(G.arcs[i][j] == MaxWeight) //两点之间无连接时权值为默认的32767,但输出时为了方便输出 "∞" { printf("%s\t","∞"); } else printf("%d\t",G.arcs[i][j]); } }}int main(){ AMGraph G; CreateUDN(G); PrintfGraph(G);}运行结果如下:
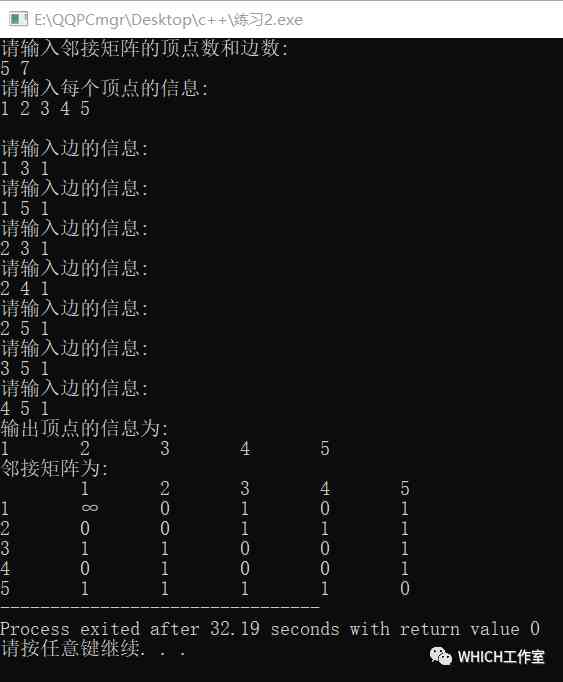
有向图的邻接矩阵:
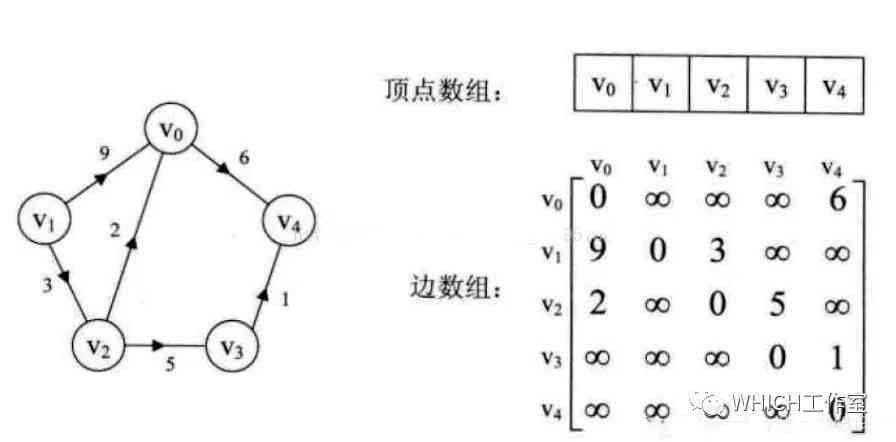
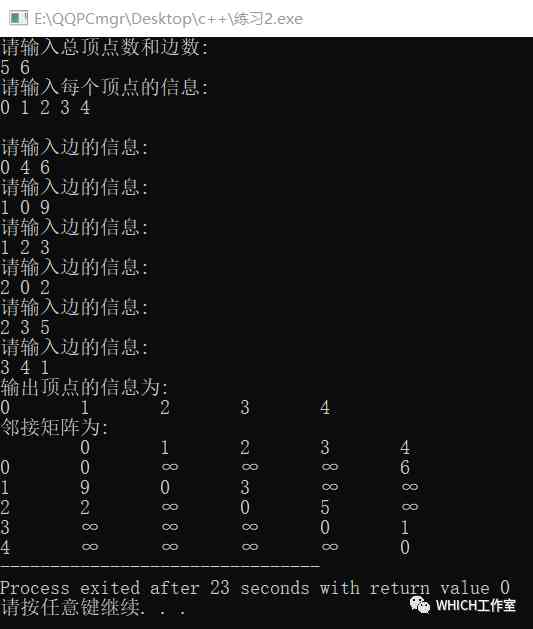
typedef struct{ int vexs[MaxVertices]; int arcs[MaxVertices][MaxVertices]; int n,e;}AMGraph;void CreateGraph(AMGraph &G){ int n,e,i,j,vi,vj,w; printf("请输入总顶点数和边数:\n"); scanf("%d %d",&G.n,&G.e); n = G.n; e = G.e; printf("请输入每个顶点的信息:\n"); for(i=0;i<n;i++) { scanf("%d",&G.vexs[i]); } for(i=0;i<n;i++) { for(j=0;j<n;j++) { if(i==j) { G.arcs[i][j] = 0; //顶点到自身的路径为0 } else { G.arcs[i][j] = MaxWeight; //除顶点到自身外,其余均设为极大值 } } } printf("\n"); //输入顶点从0开始 for(i=0;i<e;i++) { printf("请输入边的信息:\n"); scanf("%d %d %d",&vi,&vj,&w); G.arcs[vi][vj] = w; }// //输入顶点从1开始// for(i=0;i<e;i++)// {// printf("请输入边的信息:\n");// scanf("%d %d %d",&vi,&vj,&w);// G.arcs[vi-1][vj-1] = w;// }}void PrintfGraph(AMGraph G) //输出邻接矩阵的信息{ int i,j; printf("输出顶点的信息为:\n"); for(i=0; i<G.n; i++) { printf("%d\t",G.vexs[i]); } printf("\n邻接矩阵为:\n"); for(i=0; i<G.n; i++) { printf("\t%d",G.vexs[i]); } for(i=0; i<G.n; i++) { printf("\n%d\t",G.vexs[i]); for(j=0; j<G.n; j++) { if(G.arcs[i][j] == MaxWeight) //两点之间无连接时权值为默认的32767,但输出时为了方便输出 "∞" { printf("%s\t","∞"); } else printf("%d\t",G.arcs[i][j]); } }}int main(){ AMGraph G; CreateGraph(G); PrintfGraph(G);}运行结果:
本文分享自微信公众号 - WHICH工作室(which_cn)。
如有侵权,请联系 [email protected] 删除。
本文参与“OSC源创计划”,欢迎正在阅读的你也加入,一起分享。
版权声明
本文为[WHICH工作室]所创,转载请带上原文链接,感谢
https://my.oschina.net/u/4678692/blog/4708438
边栏推荐
猜你喜欢

解决IE、firefox浏览器下JS的new Date()的值为Invalid Date、NaN-NaN的问题
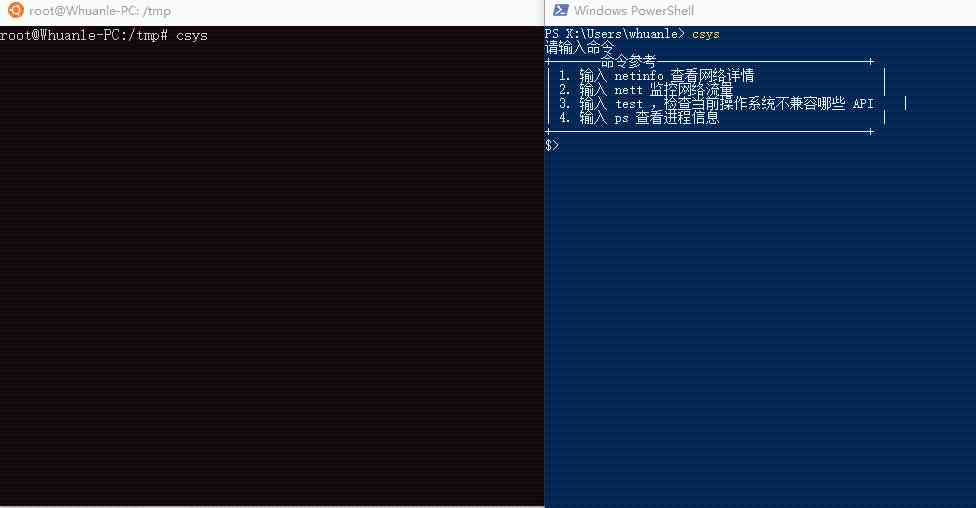
.NET Core 跨平台资源监控库及 dotnet tool 小工具
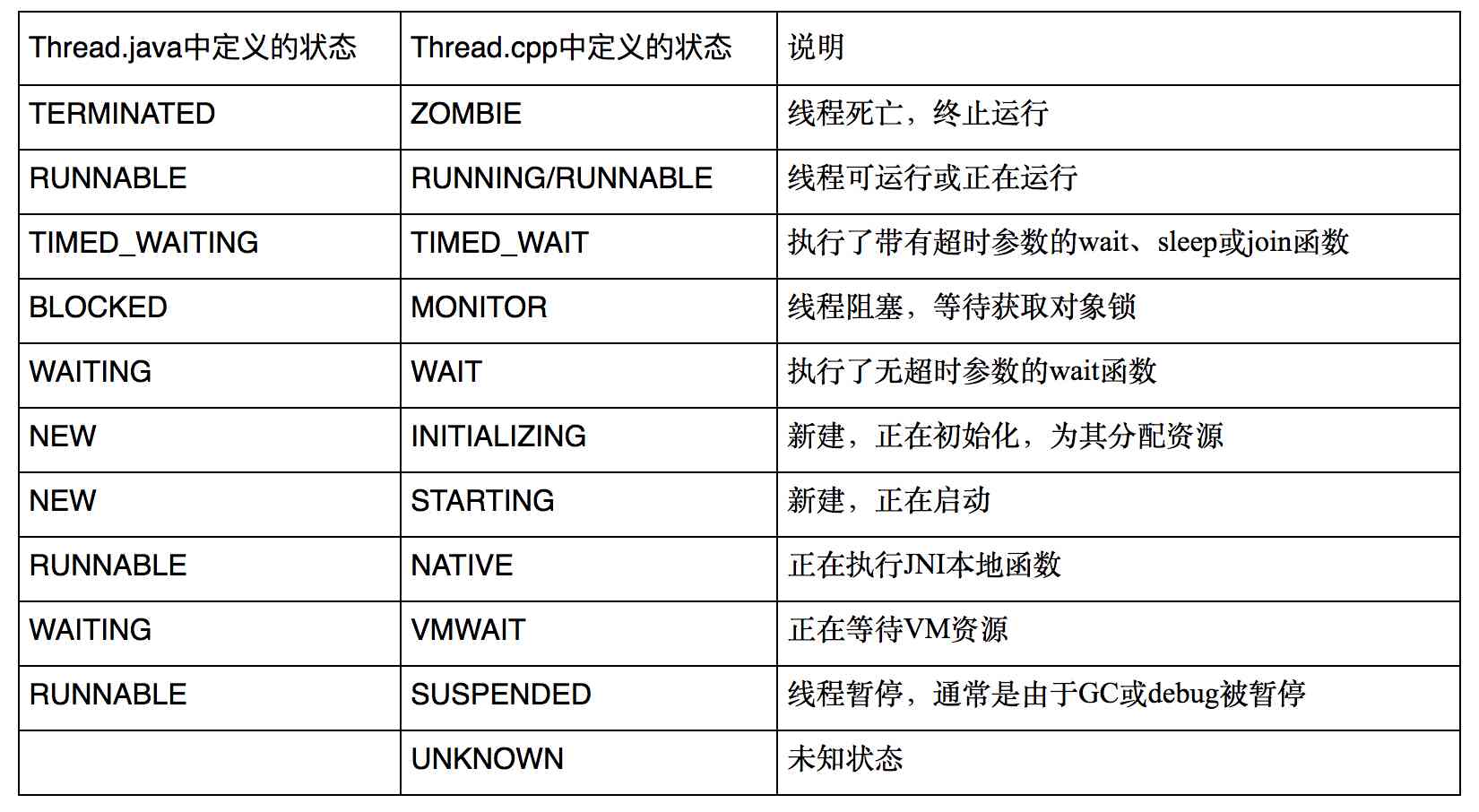
教你如何 分析 Android ANR 问题

如何让脚本同时兼容Python2和Python3?
接口测试工具Eolinker进行post请求

寻找性能更优秀的不可变小字典

Dynamic query processing method of stored procedure

Looking for a small immutable dictionary with better performance

Python features and building environment

AI人工智能编程培训学什么课程?
随机推荐
都说程序员钱多空少,程序员真的忙到没时间回信息了吗?
国内三大云数据库测试对比
Newbe.ObjectVisitor Example 1
动态规划之子序列问题解题模板
如何让脚本同时兼容Python2和Python3?
Constructors and prototypes
链表
VIM Introduction Manual, (vs Code)
Flink's datasource Trilogy 3: customization
Esockettimeout solution in request in nodejs
Come and have a look! What is the relationship between AQS and countdownlatch?
Decorator (1)
【云服务】阿里云服务器ECS实例规格那么多,如何选型?最佳实践说明
当我们聊数据质量的时候,我们在聊些什么?
API生命周期的5个阶段
数据库设计:范式与反范式
Decorator (2)
选择排序
Web上的分享(Share)API
Server side resolution of lengthfieldbasedframedecoder of GetBytes