One 、 What is the original code 、 Inverse and complement
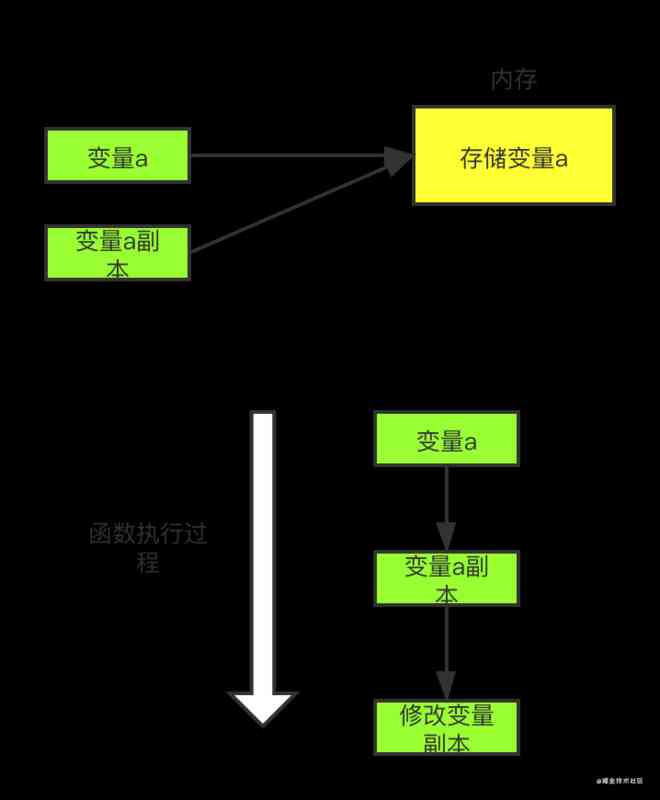
We know , The signed numbers stored inside the computer are stored in the form of complements , Performing operations in the form of complements . What is the complement of a number ? Why use complements ? This is from the number of the original code 、 The counter code begins with . Let's take integer numbers as an example , And suppose the word length is 8 position .

1、 Original code
Integers X The original code refers to : Its sign bit is 0 Express positive , by 1 Negative ; The numerical part is X The binary number of the absolute value of .X The original code of is usually used 【X】 The original meaning is . Such as :
【+100】 primary =01100100 【+0】 primary =00000000
【-100】 primary =11100100 【-0】 primary =10000000
Be careful : In the original , There are two representations of zero .
The original code representation is simple and easy to understand , And truth ( The signed number itself ) Easy to switch , As long as the symbol is restored , But when two positive numbers are subtracted or different sign numbers are added , You have to compare the absolute value of two numbers , To decide who will reduce who , To determine whether the result is positive or negative , So the original code is not easy to add and subtract .
2、 Inverse code
X The reverse code of is to refer to : For positive numbers , The reverse code is the same as the original code ; For negative numbers , The sign bits remain the same , Its number is X The absolute value of is negated (1 change 0,0 change 1).X The reverse code of is usually used 【X】 To express in reverse . Such as
【+100】 back =01100100 【+0】 back =00000000
【-100】 back =10011011【-0】 back =11111111
Be careful : In the counter code , There are also two representations of zero .
Inverse code operation is not convenient , It is usually used as an intermediate transition for complement codes .
3、 Complement code
X The complement of a is : For positive numbers , The complement code is the same as the original code ; For negative numbers , The sign bits remain the same , Its number is X The absolute value of is negated and added at the lowest order 1.X The complement of is usually used 【X】 To fill in to show , actually ,【X】 repair =【X】 back +1. Such as :
【+100】 repair =01100100 【+0】 repair =00000000
【-100】 repair =10011100 【-0】 repair =00000000
Be careful : In the complement , Zero has a unique code ,【+0】 repair =【-0】 repair =00000000.
The complement operation is simple and convenient , The sign bit can be used as a bit of data to participate in the operation , You don't have to deal with it alone ; Binary subtraction can be realized by adding its complement , Simplify the hardware circuit .

Two 、 The meaning of the complement
First , Let's take a few examples .
【 Example 1】 use 8 The number of bits and bits indicates respectively +0 and -0 .
Explain : We know , For signed Numbers , We define the highest bit as the sign bit ,0 It means a positive number ,1 A negative number . The remaining bits are numeric bits , Used to indicate the size of a number .
therefore +0 It is said to be 0000 0000, and -0 Expressed as 1000 0000.
【 Example 2】 Calculation 9-6 Result .
Explain : We know :9-6=9+(-6)=3
0000 1001
+1000 0110
1000 1111
The result is -15, Obviously wrong .
And if we use the complement to calculate ?
We know ,9 The complement of is 0000 1001,-6 The complement of is 11111010, Do the operation again ,
0000 1001
+1111 1010
1 0000 0011
The highest 1 overflow , The remaining 8 Bit binary means 3 Complement . The result is 3, correct .
【 Example 3】 Analyze the running results of the program .
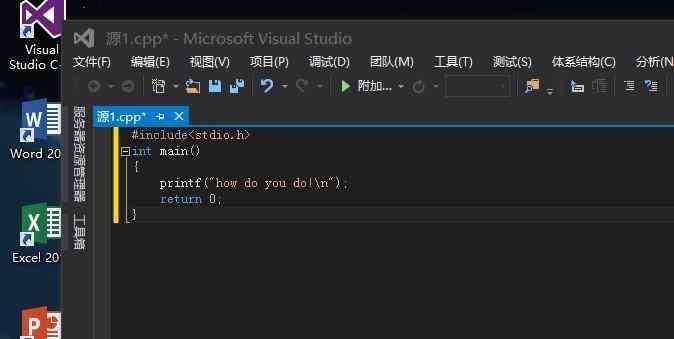
main()
{int a=100,b=-1;
Printf(“a=%d,%x,%o,%u\n”,a,a,a,a);
Printf(“b=%d,%x,%o,%u\n”,b,b,b,b);}
Running results :
a=100,64,144,100
b=-1,ffff,177777,65535
【 Example 1】 in , Why the same 0 There are two different representations ?
【 Example 2】 in , Why is the first calculation wrong , And it's right to use the complement to calculate the result ?
and 【 Example 3】 in , Why? -1 In hex 、 The results of octal and unsigned integer output become ffff,177777,65535?
This is because in a computer system , All values are represented by complements ( Storage ).
Main cause :
1、 Unified zero coding ;
2、 Unified processing of sign bit and other numerical bits ;
3、 Change subtraction into addition ;
4、 When two complement numbers are added , If the highest position ( Sign bit ) Have carry , Then carry is discarded .
3、 ... and 、 The calculation of complement
1、 Definition :
(1) A complement to a positive number : Same as the original .
【 example 1】+9 The complement of is 00001001.
(2) A negative complement : Symbol bit 1, The original code whose other bits are the absolute value of the number are reversed bit by bit ; And then add the whole number 1.
【 example 2】 seek -9 Complement .
Because the given number is negative , Then the sign bit is “1”.
The last seven :+9 The original code of (0001001)→ According to the not (1110110)→ Add 1(1110111)
therefore -7 The complement of is 11110111.
2、 Zero search
The original code is to use 1 To represent the size of a number , It belongs to positive logic , We mainly calculate the original code 1 The number of ; And the inverse code and the complement code use 0 To represent the size of a number , It belongs to negative logic , So we can take Reverse logical thinking to understand , By calculation 0 To find the complement of a negative number . Because the complement code is based on the inverse code 1, therefore 0 The number of the original number should be smaller than the absolute value of the original number 1.
for example : seek -5 Complement
The number of zeros should be 4 individual , therefore -5 The complement of is :11111011.
Again : seek -97 Complement
The number of zeros should be 96 individual ,96=64+32, The corresponding weight bits are 0, The rest are 1. therefore -97 The complement of is :10011111.
3、 Zero subtraction
A negative complement = All zeros - The original code of a positive number , Such as -5 Complement =0-5 The original code of .
Use the hexadecimal of the number , The result is converted to binary .
for example : seek -5 Complement
Algorithm 1: Algorithm 2:
00000000 00H
﹣00000101 ﹣05H
11111011 0 FBH
4、 look for 1 Law
for example : seek -15 Complement
First step :+15:00001111
The second step : Find the first one from right to left 1, And then take all the left .

11110001
Take another example to verify : seek -64 Complement
+64:01000000
11000000
Four 、 Some supplements
1、 The complement of a given number , The operation of seeking source code is divided into two cases :
(1) If the sign bit of the complement is “0”, It means a positive number , The original code is the complement code .
(2) If the sign bit of the complement is “1”, It means a negative number , So the complement of the given complement is the original code required .
【 example 3】 A complement is known as 11111001, The original code is 10000111(-7).
Because the sign bit is “1”, It means a negative number , So the bit doesn't change , Still “1”.
The other seven 1111001 Take the reverse as 0000110;
add 1, So it is 10000111.
2、 Range of values
8 The range of the number represented by the bit binary source code is -127~+127;
5、 ... and 、 summary :
1、 Original code representation
Except for the sign bit , The other bits are the absolute values of the values , This program is called “ Original code ” notation . for example :
+20 The original code of :0 000 0000 0001 0100
-20 The original code of : 1 000 0000 0001 0100
2、 Reverse code representation
Except for the sign , The inverse code of negative numbers is based on the original code and other binary inverses , The reverse code of positive numbers is the same as the original code . Such as :
+20 The inverse of is : 0 000 0000 0001 0100
-20 The inverse of is : 1 111 1111 1110 1011
3、 Complement representation
The complement of a negative number is to add... On the basis of a negative number 1, The reverse code of positive numbers is the same as the original code .
4、 Why do computers generally use complement representation
Original code 、 The inverse code and the complement code are due to three schemes for representing negative numbers , Of the three options , The source code is most suitable for multiplication and division , Complements are suitable for addition and subtraction operations , The inverse code is not very ideal in addition, subtraction, multiplication and division , Because the frequency of addition and subtraction is much higher than that of multiplication and division , So most computer systems use the complement scheme . So all the addition and subtraction operations of computers have to convert the corresponding numbers into complements , And then we do the calculation .