当前位置:网站首页>Sequence model
Sequence model
2022-07-04 08:41:00 【Doraemon AI dream】
- In the time series model , Current data is related to previously observed data
- Autoregressive models use their own past data to predict the future
- The Markov model assumes that it is currently only related to a few recent data , And then simplify the model
- Latent variable model uses latent variables to summarize historical information
Import related packages
import torch
from torch import nn
from d2l import torch as d2l
import matplotlib.pyplot as plt
Use sine function and some additive noise to generate sequence data
T = 1000 # Total points
x = torch.arange(1,T+1,dtype=torch.float32)
y = torch.sin(0.01*x)+torch.normal(0,0.2,(T,))
plt.figure(figsize=(8,4))
plt.xlim((0,1000))
plt.ylim((-1.5,1.5))
plt.xlabel('time')
plt.ylabel('y')
plt.plot(x,y)
plt.show()
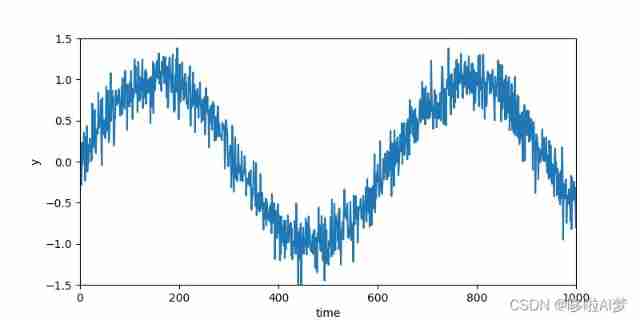
The model predicts the next time step
#PyTorch Data Iterative loading
def load_array(data_arrays,batch_size,is_train=True):
dataset = TensorDataset(*data_arrays)
return DataLoader(dataset,batch_size,shuffle=is_train)
# The sequence is transformed into a model “ features - label ”
tau = 4
features = torch.zeros((T - tau, tau))
for i in range(tau):
features[:, i] = x[i:T - tau + i]
labels = x[tau:].reshape((-1, 1))
batch_size, n_train = 16, 600
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
batch_size, is_train=True)
# Initialize the function of network weight
def init_weights(m):
if type(m) == nn.Linear:
nn.init.xavier_uniform_(m.weight)
#MPL
def get_net():
net = nn.Sequential(
nn.Linear(4,10),
nn.ReLU(),
nn.Linear(10,1)
)
net.apply(init_weights)
return net
def evaluate_loss(net, data_iter, loss):
metric = d2l.Accumulator(2) # The sum of the losses , Number of samples
for X, y in data_iter:
out = net(X)
y = y.reshape(out.shape)
l = loss(out, y)
metric.add(l.sum(), l.numel())
return metric[0] / metric[1]
# Training
def train(net,train_iter,loss,epochs,lr):
optimilizer = torch.optim.Adam(net.parameters(),lr)
for epoch in range(epochs):
for X,y in train_iter:
optimilizer.zero_grad()
l = loss(net(X),y)
l.sum().backward()
optimilizer.step()
print(f'epoch {
epoch + 1}, '
f'loss: {
evaluate_loss(net, train_iter, loss):f}')
loss = nn.MSELoss(reduction='none')
net = get_net()
train(net,train_iter,loss,10,0.01)
onestep_preds = net(features)
d2l.plot(
[time, time[tau:]],
[x.detach().numpy(), onestep_preds.detach().numpy()], 'time', 'x',
legend=['data', '1-step preds'], xlim=[1, 1000], figsize=(6, 3))
d2l.plt.show()
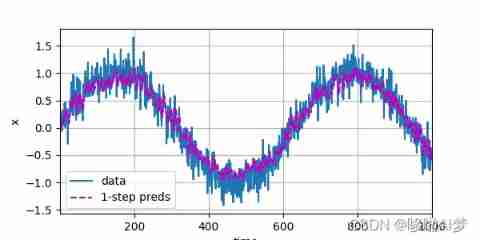
Multi step prediction
max_steps = 64
features = torch.zeros((T - tau - max_steps + 1, tau + max_steps))
for i in range(tau):
features[:, i] = x[i:i + T - tau - max_steps + 1]
for i in range(tau, tau + max_steps):
features[:, i] = net(features[:, i - tau:i]).reshape(-1)
steps = (1, 4, 16, 64)
d2l.plot([time[tau + i - 1:T - max_steps + i] for i in steps],
[features[:, (tau + i - 1)].detach().numpy() for i in steps], 'time',
'x', legend=[f'{
i}-step preds'
for i in steps], xlim=[5, 1000], figsize=(6, 3))
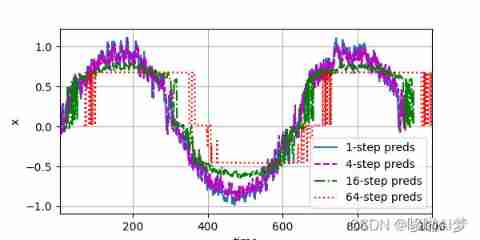
summary :
- For a causal model where time is advancing , Positive estimation usually ⽐ Reverse estimation is easier .
- For up to time steps t The sequence of observations , It is in the time step t + k The predicted output is “k Next step prediction ”. As we predict the time k An increase in value , It will cause the rapid accumulation of errors and the rapid decline of prediction quality .
边栏推荐
猜你喜欢
![Private collection project practice sharing [Yugong series] February 2022 U3D full stack class 007 - production and setting skybox resources](/img/f9/6c97697896cd1bd0f1d62542959f29.jpg)
Private collection project practice sharing [Yugong series] February 2022 U3D full stack class 007 - production and setting skybox resources
![Sports [running 01] a programmer's half horse challenge: preparation before running + adjustment during running + recovery after running (experience sharing)](/img/c8/39c394ca66348044834eb54c68c2a7.png)
Sports [running 01] a programmer's half horse challenge: preparation before running + adjustment during running + recovery after running (experience sharing)
![[CV] Wu Enda machine learning course notes | Chapter 9](/img/de/41244904c8853b8bb694e05f430156.jpg)
[CV] Wu Enda machine learning course notes | Chapter 9

L1 regularization and L2 regularization

Guanghetong's high-performance 4g/5g wireless module solution comprehensively promotes an efficient and low-carbon smart grid
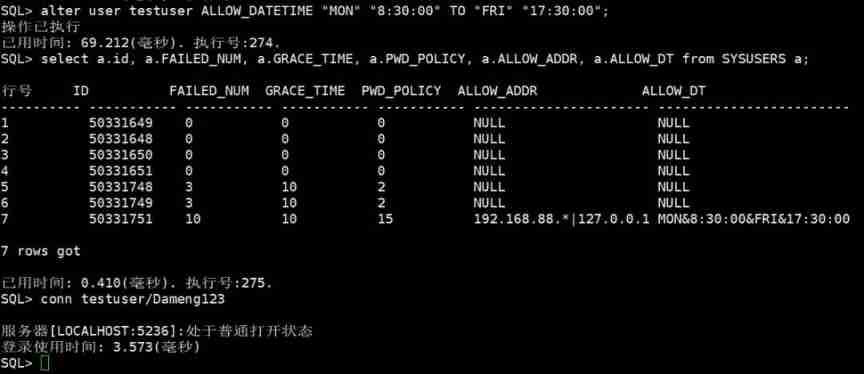
DM database password policy and login restriction settings

How to solve the problem of computer jam and slow down
From scratch, use Jenkins to build and publish pipeline pipeline project

Educational Codeforces Round 115 (Rated for Div. 2)

awk从入门到入土(12)awk也可以写脚本,替代shell
随机推荐
Leetcode topic [array] -136- numbers that appear only once
随机事件的关系与运算
DM8 tablespace backup and recovery
FRP intranet penetration, reverse proxy
ArcGIS application (XXII) ArcMap loading lidar Las format data
Codeforces Global Round 21(A-E)
Collections in Scala
How college students choose suitable computers
awk从入门到入土(18)gawk线上手册
The second session of the question swiping and punching activity -- solving the switching problem with recursion as the background (I)
C#,数值计算(Numerical Recipes in C#),线性代数方程的求解,Gauss-Jordan消去法,源代码
NewH3C——ACL
Technology sharing | MySQL parallel DDL
Three paradigms of database design
【无标题】转发最小二乘法
ctfshow web255 web 256 web257
Fault analysis | MySQL: unique key constraint failure
DM8 database recovery based on point in time
es6总结
A method for detecting outliers of data