Probabilistic linear regression with uncertain weights

flutter + Applet + Back end ,3 Individuals can open your APP The way | Registration will be sent to Dajiang Yuntai 、 Huawei watch ！>>>

author |Ruben Winastwan compile |VK source |Towards Data Science

When you study data science and machine learning , Linear regression is probably the first statistical method you've come across . I guess this is not the first time you've used linear regression . therefore , In this paper , I want to talk about probabilistic linear regression , Instead of the typical / Deterministic linear regression .

But before that , Let's briefly discuss the concept of deterministic linear regression , In order to quickly understand the main points of this article .

Linear regression is a basic statistical method , Used to create one or more input variables ( Or independent variable ) With one or more output variables ( Or dependent variable ) The linear relationship between .

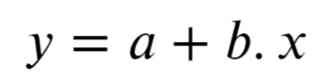
In the above formula ,a Is the intercept ,b Is the slope .x It's an independent variable ,y It's a dependent variable , That's what we're going to predict .

a and b A gradient descent algorithm is used to optimize the value of . then , We get an optimal regression line between the independent variable and the dependent variable . Through the regression line , We can predict any input x Of y Value . These are the steps of how to establish a typical or deterministic linear regression algorithm .

However , This deterministic linear regression algorithm does not really describe the data . Why is that ?

actually , When we do linear regression analysis , There are two kinds of uncertainties :

• Arbitrary uncertainty , That is, the uncertainty created by the data .
• Cognitive uncertainty , This is the uncertainty that comes from regression models .

I will elaborate on these uncertainties in this article . Considering these uncertainties , Probability linear regression should be used instead of deterministic linear regression .

In this paper , We will discuss probabilistic linear regression and its difference from deterministic linear regression . We'll first see how deterministic linear regression works in TensorFlow Built in , Then we'll continue to build a containing TensorFlow Probability linear regression model of probability .

First , Let's start by loading the dataset that will be used in this article .

Loading and preprocessing data

The dataset to be used in this article is car Of MPG Data sets . As usual , We can use pandas Load data .

import pandas as pd

auto_data = pd.read_csv('auto-mpg.csv')
auto_data.head()

Here is a statistical summary of the data .

Next , We can use the following code to see the correlation between variables in the dataset .

import matplotlib.pyplot as plt
import seaborn as sns

corr_df = auto_data.corr()

sns.heatmap(corr_df, cmap="YlGnBu", annot = True)
plt.show()

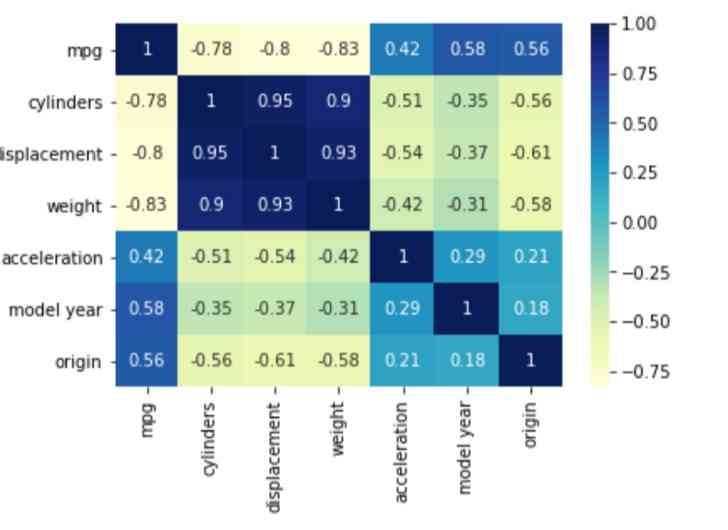
Now if we look at the correlation , Miles per gallon of a car (MPG) There is a strong negative correlation with the weight of the car .

In this paper , For visualization purposes , I'm going to do a simple linear regression analysis . The independent variable is the weight of the car , The dependent variable is the car MPG.

Now? , Let's use it Scikit-learn Decompose the data into training data and test data . After splitting the data , We can now scale dependent and independent variables . This is to ensure that the two variables are in the same range, which will also improve the convergence rate of the linear regression model .

from sklearn import preprocessing
from sklearn.model_selection import train_test_split

x = auto_data['weight']
y = auto_data['mpg']

x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.2, random_state=5)

min_max_scaler = preprocessing.MinMaxScaler()

x_train_minmax = min_max_scaler.fit_transform(x_train.values.reshape(len(x_train),1))
y_train_minmax = min_max_scaler.fit_transform(y_train.values.reshape(len(y_train),1))
x_test_minmax = min_max_scaler.fit_transform(x_test.values.reshape(len(x_test),1))
y_test_minmax = min_max_scaler.fit_transform(y_test.values.reshape(len(y_test),1))

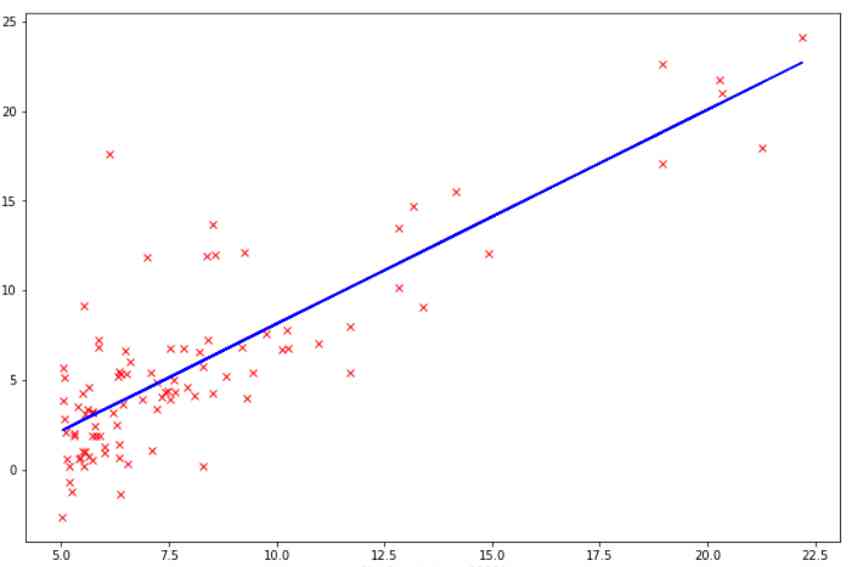
Now if we visualize the training data , We get the following Visualization :

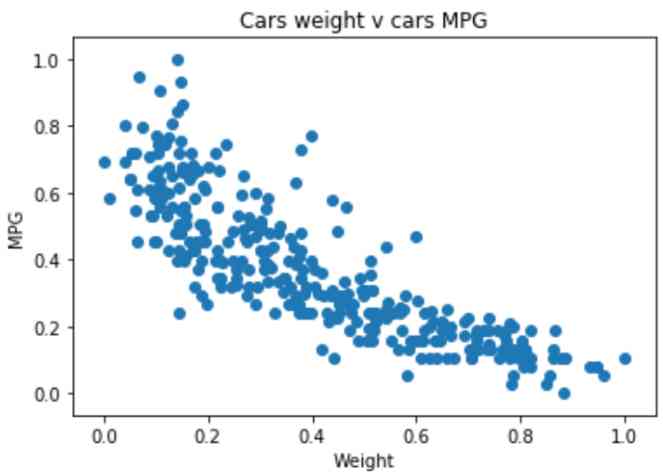
fantastic ! Next , Let's continue to use TensorFlow Construct our deterministic linear regression model .

---

be based on TensorFlow The deterministic linear regression of

use TensorFlow It is very easy to establish a simple linear regression model . All we need to do is build a single full connection layer model without any activation functions . For the cost function , The mean square error is usually used . In this case , I will use RMSprop As an optimizer , The model will be in 100 individual epoch Train inside . We can use the following lines of code to build and train the model .

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras.losses import MeanSquaredError

model = Sequential([
    Dense(units=1, input_shape=(1,))
])

model.compile(loss=MeanSquaredError(), optimizer=RMSprop(learning_rate=0.01))
history = model.fit(x_train_minmax, y_train_minmax, epochs=100, verbose=False)

After we trained the model , Let's look at the loss of the model to check the convergence of the loss .

def plot_loss(history):
    
  plt.plot(history.history['loss'], label='loss')
  plt.xlabel('Epoch')
  plt.ylabel('Error')
  plt.legend()
  plt.grid(True)
  
plot_loss(history)

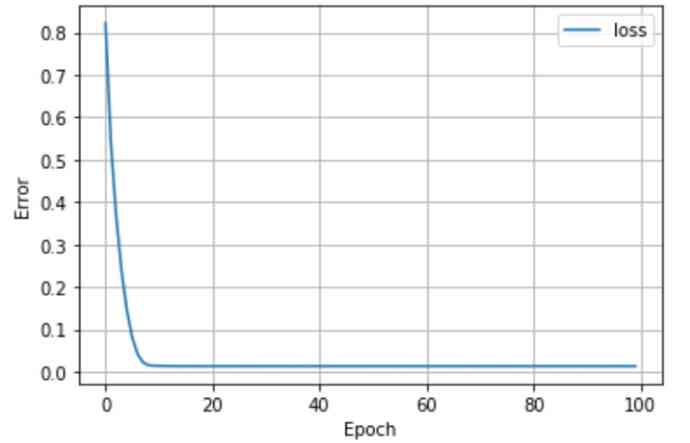
It seems that the losses have converged . Now? , If we use trained models to predict test sets , We can see the regression line below .

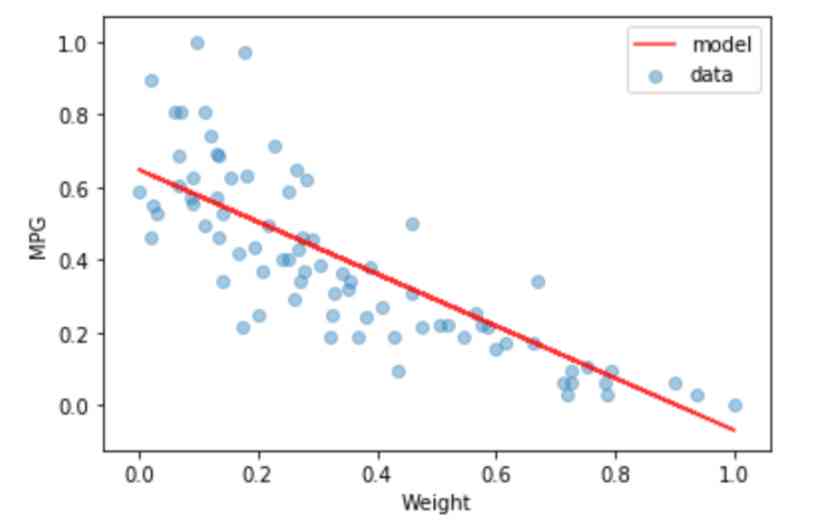
this is it . We finished !

As I mentioned earlier , Use TensorFlow It's very easy to build a simple linear regression model . With the regression line , We can now enter any given weight of the car to approximate the car's MPG. for instance , Suppose the weight of the car after feature scaling is 0.64. By passing this value to the trained model , We can get the corresponding car MPG value , As shown below .

Now you can see , The model predicts the car's MPG yes 0.21. In short , For any given car weight , We got a certain car MPG value

However , The output doesn't tell the whole story . Here we should pay attention to two things . First , We have limited data points . second , As we can see from the linear regression graph , Most data points are not really on the regression line .

Although the output we get is 0.21, But we know about the actual car MPG Not exactly 0.21. It can be a little lower than that , It can also be slightly higher than this value . let me put it another way , Uncertainty needs to be taken into account . This uncertainty is called arbitrary uncertainty .

Deterministic linear regression cannot capture any uncertainty of data . To capture this arbitrary uncertainty , We can use probabilistic linear regression instead of .

TensorFlow Probability linear regression of probability

Because of TensorFlow probability , It's also very easy to build probabilistic linear regression models . however , You need to install first tensorflow_probability library . You can use pip Command to install it , As shown below :

pip install tensorflow_probability

A prerequisite for installing this library is that you need to have TensorFlow 2.3.0 edition . therefore , Please make sure to install TensorFlow Probability Before upgrading your TensorFlow edition .

A probabilistic linear regression model is established for uncertainty

In this section , We will establish a probabilistic linear regression model considering uncertainty .

This model is very similar to deterministic linear regression . however , Instead of just using a single full connectivity layer , We need to add another layer as the last layer . The last layer converts the final output value from certainty to probability distribution .

In this case , We're going to create the last layer , It converts the output value to the probability value of the normal distribution . Here's how it works .

import tensorflow_probability as tfp
import tensorflow as tf
tfd = tfp.distributions
tfpl = tfp.layers

model = Sequential([
  Dense(units=1+1, input_shape=(1,)),
  tfpl.DistributionLambda(
      lambda t: tfd.Normal(loc=t[..., :1],
                           scale=tf.math.softplus(t[...,1:]))),
])

Be careful , We applied an extra layer at the end TensorFlow Probability layer . This layer will connect the two outputs of the previous full connection layer ( One is the mean , One is the standard deviation ) To have a trainable mean (loc) And standard deviation (scale) The probability value of the normal distribution .

We can use RMSprop As an optimizer , But if you want to , You can also use other optimizers . For the loss function , We need to use negative log likelihood .

But why do we use negative log likelihood as a loss function

Negative log likelihood as a cost function

In order to fit some data into a distribution , We need to use the likelihood function . Through the likelihood function , We're given that we're trying to estimate unknown parameters in the data ( for example , The mean and standard deviation of normal distribution data ).

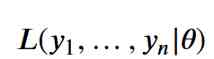
In our probabilistic regression model , The job of the optimizer is to find the maximum likelihood estimate of the unknown parameter . let me put it another way , We train the model to find the most likely parameter value from our data .

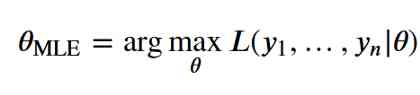
Maximizing likelihood estimation is the same as minimizing negative log likelihood . In the field of optimization , Usually the goal is to minimize costs, not maximize costs . That's why we use negative log likelihood as a cost function .

Here is the implementation of the negative log likelihood as our custom loss function .

def negative_log_likelihood(y_true, y_pred):
    
    return -y_pred.log_prob(y_true)

The training and prediction results of stochastic uncertainty probability linear regression model

Now that we've built the model and defined the optimizer and loss function , Now let's compile and train the model .

model.compile(optimizer=RMSprop(learning_rate=0.01), loss=negative_log_likelihood)
history = model.fit(x_train_minmax, y_train_minmax, epochs=200, verbose=False);

Now we can take samples from trained models . We can visualize the comparison between the test set and the example generated from the model through the following code .

y_model = model(x_test_minmax)
y_sample = y_model.sample()

plt.scatter(x_test_minmax, y_test_minmax, alpha=0.5, label='test data')
plt.scatter(x_test_minmax, y_sample, alpha=0.5, color='green', label='model sample')
plt.xlabel('Weight')
plt.ylabel('MPG')
plt.legend()
plt.show()

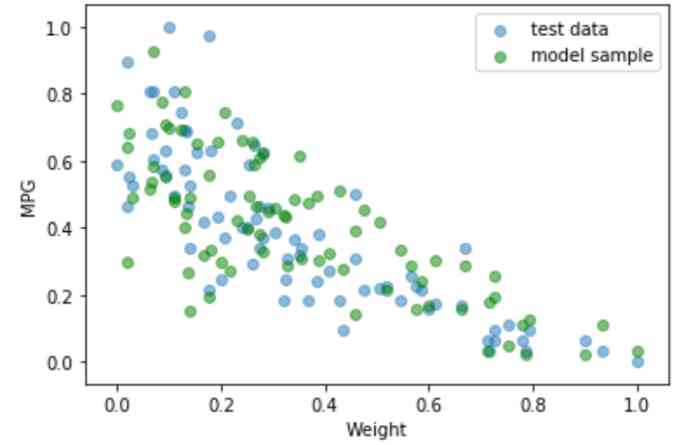
As you can see from the visualization above , Now for any given input value , The model does not return deterministic values . contrary , It will return a distribution , And draw a sample based on the distribution .

If you compare test set data points ( Blue dot ) And the data points predicted by the training model ( Green dot ), You might think that green dots and blue dots come from the same distribution .

Next , We can also visualize the mean and standard deviation of the distribution generated by the training model , Given the data in the training set . We can do this by applying the following code .

y_mean = y_model.mean()
y_sd = y_model.stddev()
y_mean_m2sd = y_mean - 2 * y_sd
y_mean_p2sd = y_mean + 2 * y_sd

plt.scatter(x_test_minmax, y_test_minmax, alpha=0.4, label='data')
plt.plot(x_test_minmax, y_mean, color='red', alpha=0.8, label='model $\mu$')
plt.plot(x_test_minmax, y_mean_m2sd, color='green', alpha=0.8, label='model $\mu \pm 2 \sigma$')
plt.plot(x_test_minmax, y_mean_p2sd, color='green', alpha=0.8)
plt.xlabel('Weight')
plt.ylabel('MPG')
plt.legend()
plt.show()

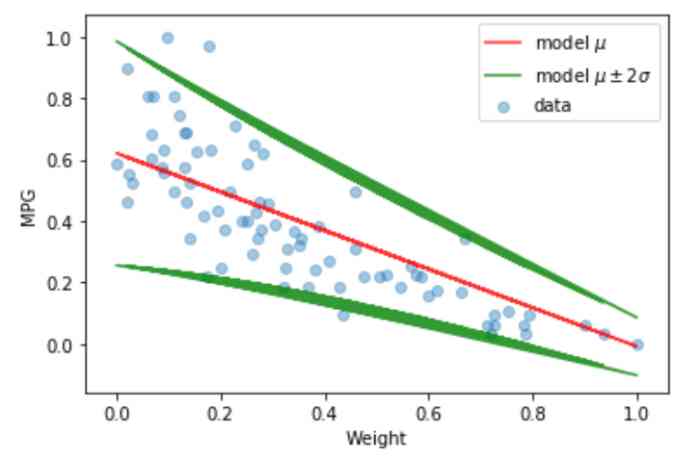
We can see , Probabilistic linear regression models give us more than regression lines . It also gives an approximation of the standard deviation of the data . It can be seen that , about 95% The data points of the test set are in the range of two standard deviations .

Establish a probabilistic linear regression model of random and cognitive uncertainty

up to now , We've built a probabilistic regression model , It takes into account the uncertainty from the data , Or we call it arbitrary uncertainty .

However , In reality , We also need to deal with the uncertainty from the regression model itself . Due to the imperfection of the data , There is also uncertainty in the weight or slope of regression parameters . This uncertainty is called cognitive uncertainty .

up to now , Our probability model only considers a certain weight . As you can see from Visualization , The model only generates a regression line , And it's usually not exactly accurate .

In this section , We will improve the probabilistic regression model which considers both arbitrary and cognitive uncertainties . We can use Bayesian view to introduce the uncertainty of regression weights .

First , Before we see the data , We need to define our previous view of weight distribution . Usually , We don't know what's going to happen , Right ? For the sake of simplicity , We assume that the distribution of weights is normal and the mean value is 0, The standard deviation is 1.

def prior(kernel_size, bias_size, dtype=None):
  n = kernel_size + bias_size
  return Sequential([
      tfpl.DistributionLambda(lambda t: tfd.Independent(
          tfd.Normal(loc=tf.zeros(n), scale=tf.ones(n))))
  ])

Because we hard coded the mean and the standard deviation , This priori is untreatable .

Next , We need to define a posterior distribution of regression weights . A posterior distribution shows how our beliefs change when we see patterns in the data . therefore , The parameters in the posterior distribution are trainable . Here's the code implementation that defines a posteriori distribution .

def posterior(kernel_size, bias_size, dtype=None):
  n = kernel_size + bias_size
  return Sequential([
      tfpl.VariableLayer(2 * n, dtype=dtype),
      tfpl.DistributionLambda(lambda t: tfd.Independent(
          tfd.Normal(loc=t[..., :n],
                     scale=tf.nn.softplus(t[..., n:]))))
  ])

The problem now is , What is the definition of the variable in this posterior function ? The idea behind this variable layer is that we're trying to get close to the real posterior distribution . In general , It is impossible to derive a true posterior distribution , So we need to approximate it .

After defining a priori function and a posteriori function , We can establish a probabilistic linear regression model with weight uncertainty . Here's the code implementation .

model = Sequential([
    tfpl.DenseVariational(units = 1 + 1, 
                          make_prior_fn = prior,
                          make_posterior_fn = posterior,
                          kl_weight=1/x.shape[0]),
    tfpl.DistributionLambda(
      lambda t: tfd.Normal(loc=t[..., :1],
                           scale=tf.math.softplus(t[...,1:])))
])

As you may have noticed , The only difference between this model and the previous probabilistic regression model is the first level . We use it DenseVariational Layer instead of the normal full connection layer . In this layer , We use the functions before and after as parameters . The second layer is exactly the same as the previous model .

Training and prediction results of probabilistic linear regression models with random uncertainty and cognitive uncertainty

Now it's time to compile and train the model .

The optimizer and cost function are still the same as the previous model . We use RMSprop As optimizer and negative log likelihood as our cost function . Let's compile and train .

model.compile(optimizer= RMSprop(learning_rate=0.01), loss=negative_log_likelihood)
history = model.fit(x_train_minmax, y_train_minmax, epochs=500, verbose=False);

Now it's time to visualize the uncertainty of the weights or slopes of regression models . The following is the code implementation of the visualization results .

plt.scatter(x_test_minmax, y_test_minmax, marker='.', alpha=0.8, label='data')
for i in range(10):
    y_model = model(x_test_minmax)
    y_mean = y_model.mean()
    y_mean_m2sd = y_mean - 2 * y_model.stddev()
    y_mean_p2sd = y_mean + 2 * y_model.stddev()
    
    if i == 0:
        plt.plot(x_test_minmax, y_mean, color='red', alpha=0.8, label='model $\mu$')
        plt.plot(x_test_minmax, y_mean_m2sd, color='green', alpha=0.8, label='model $\mu \pm 2 \sigma$')
        plt.plot(x_test_minmax, y_mean_p2sd, color='green', alpha=0.8)
    else:
        plt.plot(x_test_minmax, y_mean, color='red', alpha=0.8)
        plt.plot(x_test_minmax, y_mean_m2sd, color='green', alpha=0.8)
        plt.plot(x_test_minmax, y_mean_p2sd, color='green', alpha=0.8)
plt.xlabel('Weight')
plt.ylabel('MPG')
plt.legend()
plt.show()

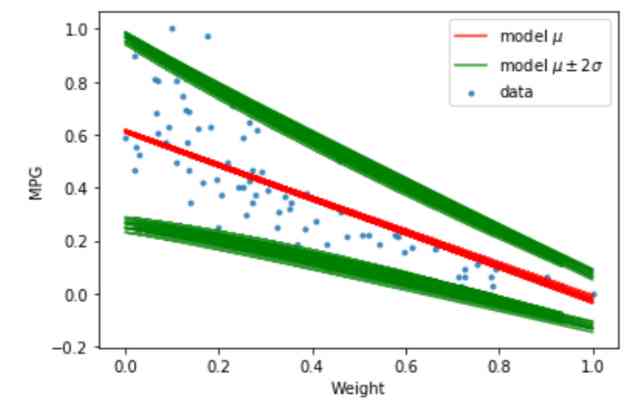
In the visualization above , You can see , The posterior distribution of the trained model produces a linear line ( mean value ) And the standard deviation is different in each iteration . All of these lines are reasonable solutions to fit the data points in the test set . however , Because of cognitive uncertainty , We don't know which line is the best .

Usually , The more data points we have , The less uncertainty we see in the regression line .

---

Tonight?

Now you've seen the difference between probabilistic linear regression and deterministic linear regression . In probabilistic linear regression , Two kinds of uncertainty arise from data ( arbitrarily ) And regression models ( cognition ) Can be taken into account .

If we want to build a deep learning model , Let inaccurate predictions lead to very serious negative consequences , For example, in the field of autonomous driving and medical diagnosis , It's very important to consider these uncertainties .

Usually , When we have more data points , The cognitive uncertainty of the model will be reduced .

Link to the original text ：https://towardsdatascience.com/probabilistic-linear-regression-with-weight-uncertainty-a649de11f52b

Welcome to join us AI Blog station ： http://panchuang.net/

sklearn Machine learning Chinese official documents ： http://sklearn123.com/

Welcome to pay attention to pan Chuang blog resource summary station ： http://docs.panchuang.net/