After reading this article , You can go and get the following questions :
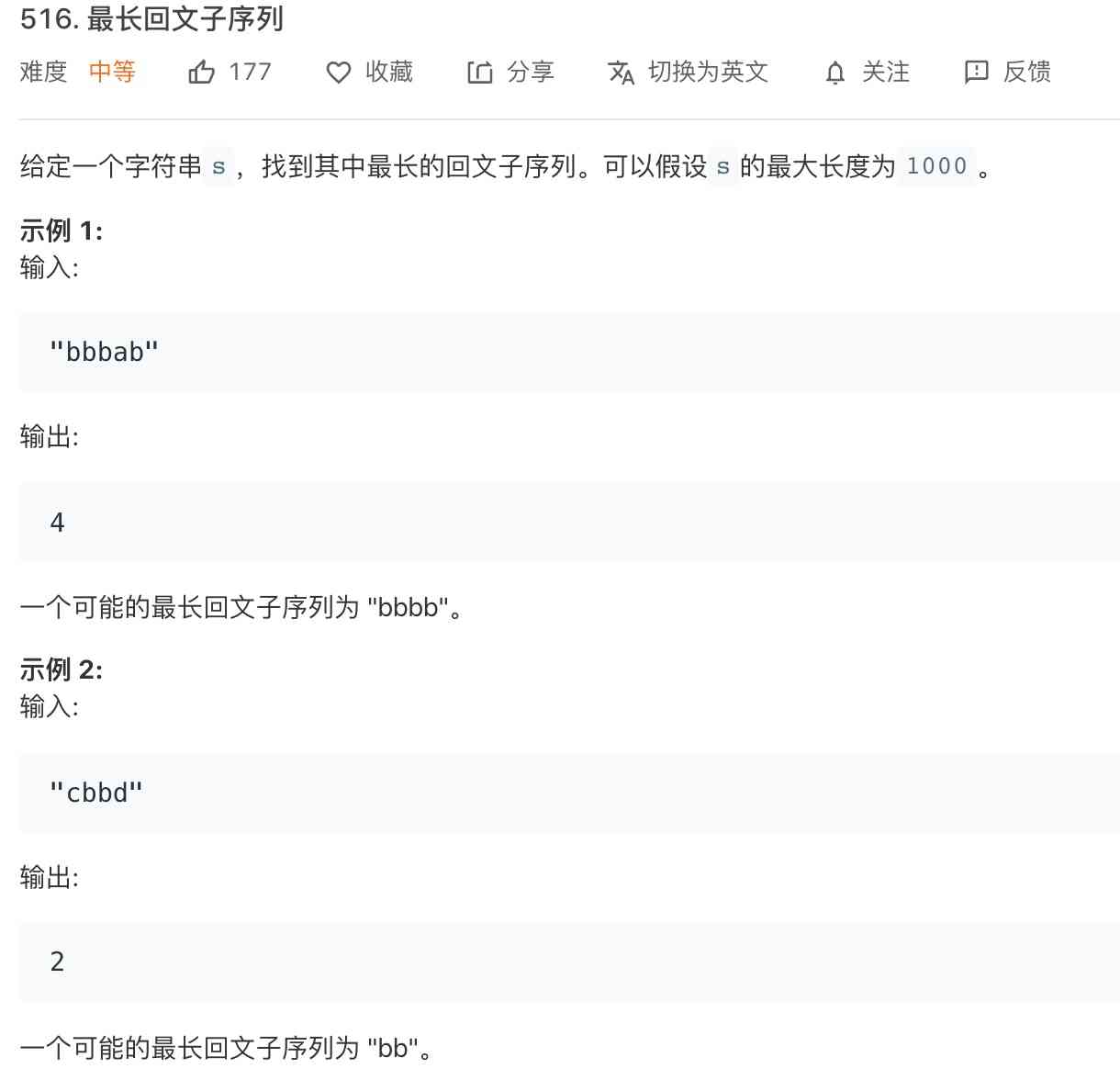
516. The longest palindrome subsequence
-----------
Subsequence problem is a common algorithm problem , And it's not easy to solve .
First , Subsequence problem itself is relative to substring 、 Subarrays are more difficult , Because the former is a discontinuous sequence , The latter two are continuous , Even if you are poor, you will not , Let alone solve the related algorithm problem .
and , The subsequence problem is likely to involve two strings , For example 「 Longest common subsequence 」, If there is no certain experience in handling , It's really not easy to come up with . Therefore, this paper will take a look at the subsequence problem , There are actually two templates , If you think about these two ways of thinking about the relevant problems , as sure as a gun .
Generally speaking , All these questions are for you to ask for one The longest subsequence , Because the shortest subsequence is a character , There's nothing to ask . Once the sub sequence and the maximum value are involved , That's almost certain , It is dynamic planning techniques , Time complexity is generally O(n^2).
The reason is simple , You think about a string , How many possibilities are its subsequences ? At least it's exponential , In this case , Don't use dynamic planning techniques , What else do you want to do ?
Since we have to use dynamic programming , Then define dp Array , Find a state transition relationship . Two ideas we're talking about , Namely dp How to define arrays . Different questions may need different dp Array definition to solve .
One 、 Two ways of thinking
1、 The first idea template is a one-dimensional dp Array :
int n = array.length;
int[] dp = new int[n];
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
dp[i] = The most value (dp[i], dp[j] + ...)
}
}
Take an example we wrote 「 The longest increasing subsequence 」, In this way of thinking dp The definition of an array is :
In subarray array[0..i] in , We need subsequences ( The longest increasing subsequence ) Is the length of the dp[i].
Why the longest increaser needs this kind of thinking ? The previous article is very clear , Because it is in line with induction , You can find the relationship of state transfer , It's not going to be specific here .
2、 The second idea template is a two-dimensional dp Array :
int n = arr.length;
int[][] dp = new dp[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (arr[i] == arr[j])
dp[i][j] = dp[i][j] + ...
else
dp[i][j] = The most value (...)
}
}
This kind of thinking is used relatively more , Especially when it comes to two strings / Subsequences of arrays , For example, as mentioned above 「 Longest common subsequence 」. In this idea dp The meaning of array is divided into 「 Only one string involved 」 and 「 It involves two strings 」 Two cases .
PS: I've seriously written about 100 Multiple original articles , Hand brush 200 Daoli is the subject , All published in labuladong A copy of the algorithm , Continuous updating . Recommended collection , Write the title in the order of my article , Master all kinds of algorithm set, then put into the sea of questions, like fish .
2.1 It involves two strings / Array time ( For example, the longest common subsequence ),dp The meaning of array is as follows :
In subarray arr1[0..i] And subarray arr2[0..j] in , We need subsequences ( Longest common subsequence ) The length is dp[i][j].
2.2 Only one string involved / Array time ( For example, the longest palindrome subsequence in this paper ),dp The meaning of array is as follows :
In subarray array[i..j] in , We need subsequences ( The longest palindrome subsequence ) The length of is dp[i][j].
In the first case, we can refer to these two old articles :「 Edit distance 」「 Common subsequence 」
Let's borrow the longest palindrome subsequence , Explain how to use dynamic programming in the second case .
Two 、 The longest palindrome subsequence
It was solved before 「 Longest text substring 」 The problem of , This time it's more difficult , Find the length of the longest palindrome subsequence :
We say the problem is right dp The definition of an array is : In substring s[i..j] in , The longest length of the palindrome subsequence is dp[i][j]. You have to remember this definition to understand algorithms .
Why does this problem define two-dimensional dp Array? ? We have mentioned many times before that , Finding state transfer requires inductive thinking , To put it bluntly, it is how to deduce the unknown from known results , This definition is easy to generalize , It's easy to find state transfer relationships .
say concretely , If we want to ask for dp[i][j], Suppose you know the sub problem dp[i+1][j-1] Result (s[i+1..j-1] The length of the longest palindrome subsequence in ), Can you figure out how to figure out dp[i][j] Value (s[i..j] in , The length of the longest palindrome subsequence ) Well ?
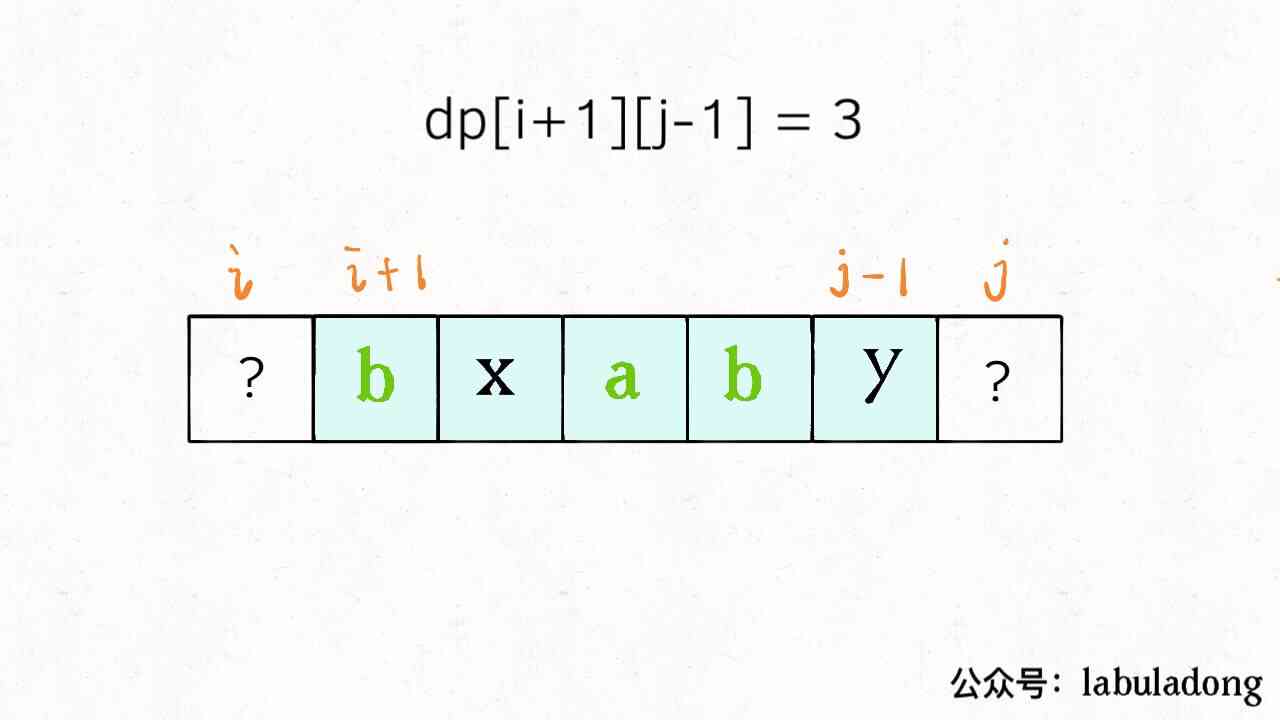
Sure ! It depends. s[i] and s[j] The characters of :
If they are equal , So it's two plus s[i+1..j-1] The longest sequence of palindrome in is s[i..j] The longest palindrome subsequence of :
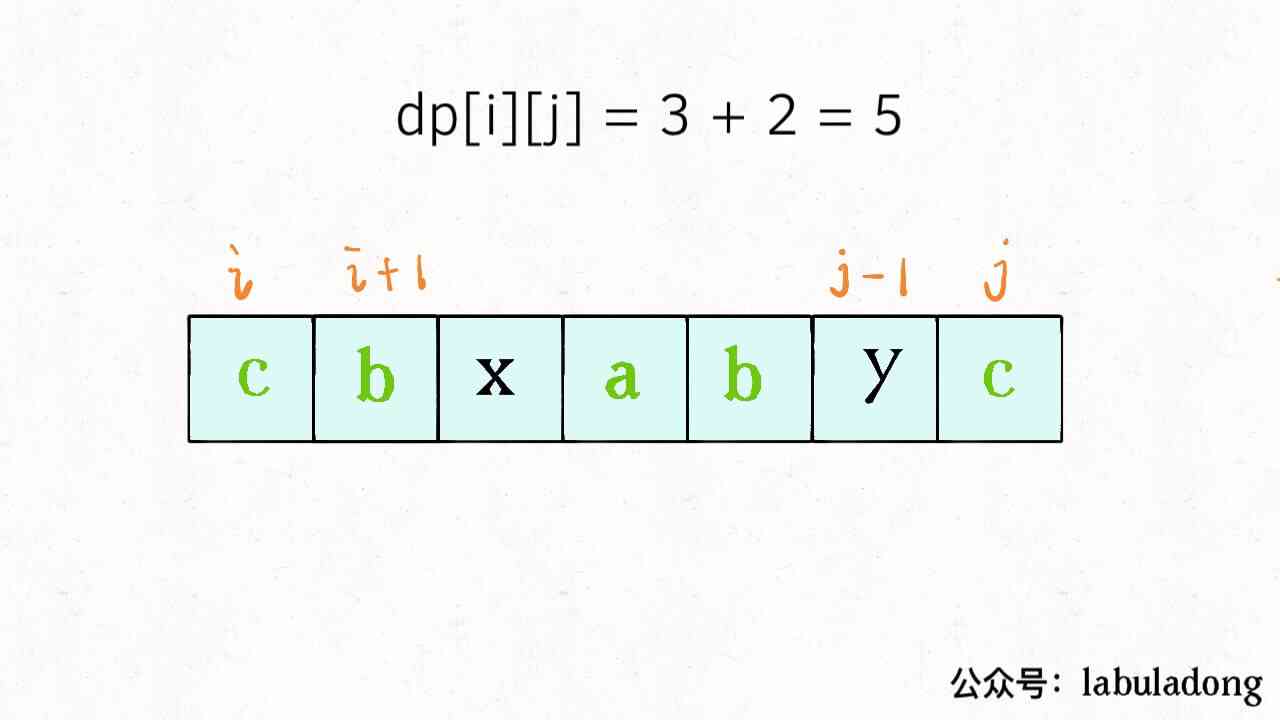
If it's not equal , It's two of them It can't be at the same time Appear in the s[i..j] In the longest palindrome subsequence of , So take them both , respectively, Join in s[i+1..j-1] in , See which substring produces a longer palindrome sequence :

The above two cases of code is like this :
if (s[i] == s[j])
// They must be in the longest palindrome subsequence
dp[i][j] = dp[i + 1][j - 1] + 2;
else
// s[i+1..j] and s[i..j-1] Whose palindrome subsequence is longer ?
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
thus , The equation of state transfer is written out , according to dp Definition of array , What we want is dp[0][n - 1], That is the whole s The length of the longest palindrome subsequence of .
3、 ... and 、 Code implementation
First, make it clear base case, If there is only one character , Obviously, the longest palindrome subsequence length is 1, That is to say dp[i][j] = 1 (i == j).
because i It must be less than or equal to j, So for those i > j The location of , There is no substequence at all , It should be initialized to 0.
in addition , Look at the state transition equation we just wrote , Want to ask for dp[i][j] Need to know dp[i+1][j-1],dp[i+1][j],dp[i][j-1] These three positions ; And then look at what we're sure about base case, fill dp The array is followed by this :
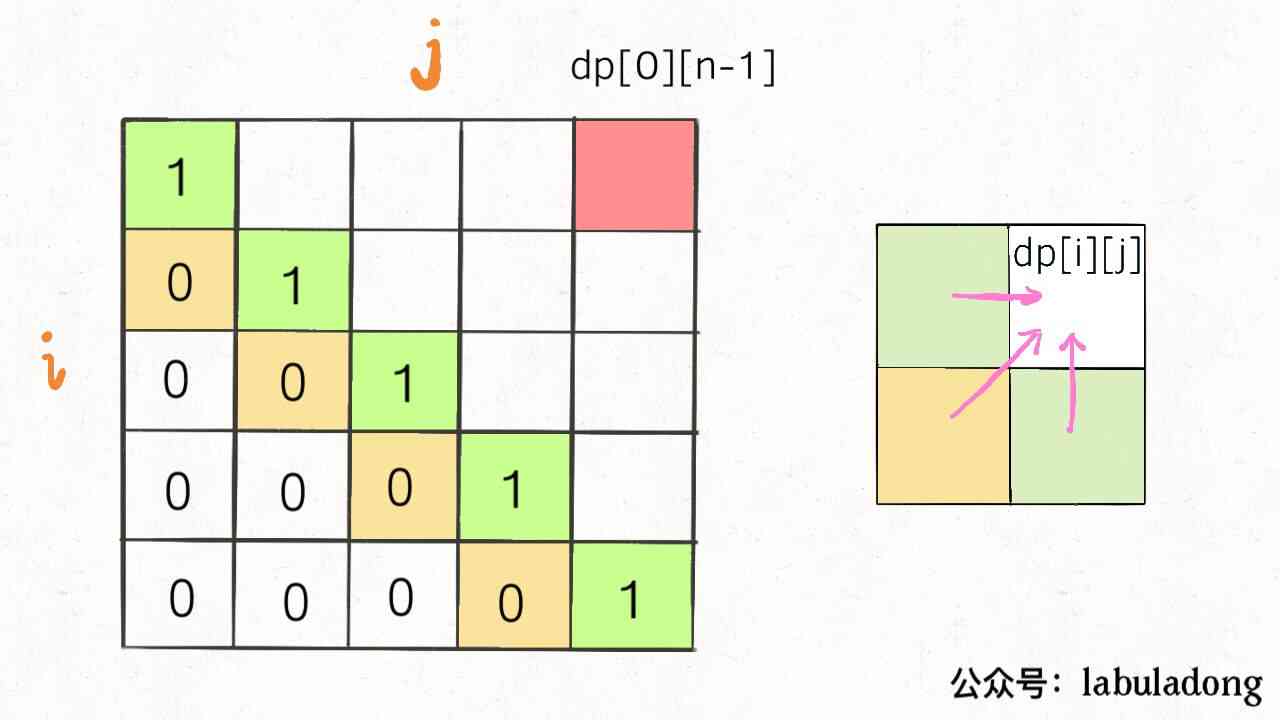
To ensure that every calculation dp[i][j], The position of the lower left and the right has been calculated , You can only traverse sideways or backwards :
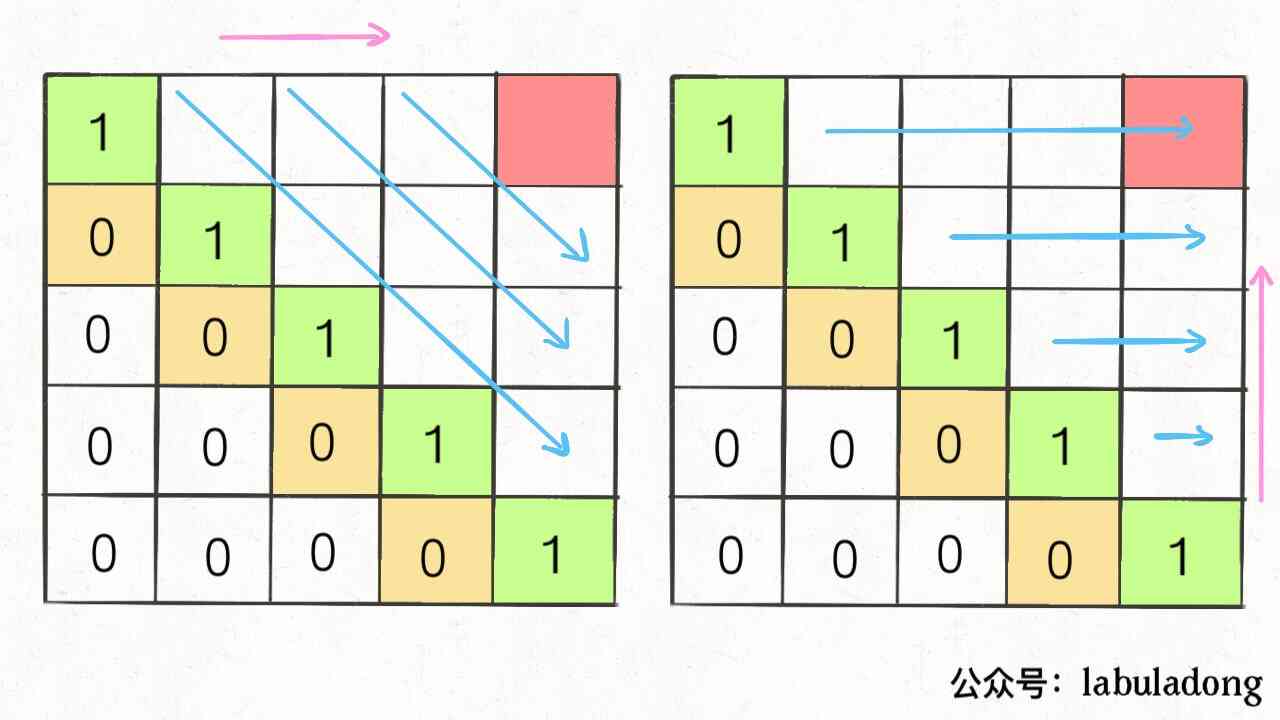
I choose to traverse backwards , The code is as follows :
int longestPalindromeSubseq(string s) {
int n = s.size();
// dp The array is all initialized to 0
vector<vector<int>> dp(n, vector<int>(n, 0));
// base case
for (int i = 0; i < n; i++)
dp[i][i] = 1;
// Reverse traversal ensures correct state transition
for (int i = n - 1; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
// State transition equation
if (s[i] == s[j])
dp[i][j] = dp[i + 1][j - 1] + 2;
else
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
}
// Whole s The longest palindrome substring length of
return dp[0][n - 1];
}
thus , The problem of the longest palindrome subsequence is solved .
_____________
my Online e-books Yes 100 Original articles , Hands with brushes 200 Daoli is the subject , Recommended collection ! Corresponding GitHub Algorithm Repository We've got it 70k star, Welcome to mark star !