当前位置:网站首页>第一部分——第1章概述
第一部分——第1章概述
2020-11-08 17:48:00 【李隶浩】
数据结构简介
使用数据结构的三个原因:效率、抽象、重用性
算法简介:效率、抽象、重用性
算法设计的一般方法:随机法、分治法、动态规划、贪心法、近似法
算法设计的一般方法
随机法
随机法依赖于随机数的统计特性。比如应用随机法的例子是快速排序。
分治法
分治法包含3个步骤:分解、求解、合并。一个分治法的例子是归并排序
动态规划
动态规划同分治法类似,都是将较大的问题分解为子问题最后再将结果合并。
不同之处,在动态规划中,处理问题的方式与子问题之间的关系有关。在分治法中,每一个子问题都是独立的。
因此,在分治法中可以以递归(第3章)的方式解决每一个子问题,然后将结果与其他子问题的结果合并。
贪心法
贪心法在求解问题时总能够做出在当前的最佳选择。换句话说,不是从整体最优上考虑,而仅仅是在某种意义上的局部最优解。
采用贪心法的例子是霍夫曼编码(第14章),是一个数据压缩算法。
霍夫曼编码中最重要的部分是构建一颗霍夫曼树(又称最优二叉树)。
- (1)为了构建一颗霍夫曼树,从它的叶子节点自底向上处理。将每个压缩的符号和它们在数据中出现的次数(频率)一起作为二叉树的根节点保存。
- (2)接下来,选择两颗拥有最小频率值得根节点作为左右子树节点,构造一颗新的二叉树,且保证新的二叉树根节点的频率值为左右子树节点的频率值之和。
- (3)然后重复这个步骤,知道得到唯一的一棵树,这就是最终的霍夫曼树。
霍夫曼树的根节点包含数据中符号的总数,叶子节点包含原始的符号以及它们出现的频率。
霍夫曼编码是一种贪心算法,因为每次它都会挑选出当前最合适的两棵树来合并。
近似法
近似法并不计算出最优解,相反,它只计算出“足够好”的解。通常利用近似法解决那些计算成本很高又因为其本身十分有价值而不愿放弃的问题。
推销员问题(第16章)是一个通常会用近似法去解决的问题。
版权声明
本文为[李隶浩]所创,转载请带上原文链接,感谢
https://my.oschina.net/u/4445379/blog/4708292
边栏推荐
- Liteos message queuing
- 构建者模式(Builder pattern)
- What is forsage Ethereum smart contract? What is the global decline of Ethereum
- uni-app实战仿微信app开发
- Using k3s to create local development cluster
- 第二章编程练习
- Talking about, check the history of which famous computer viruses, 80% of the people do not know!
- 机械硬盘随机IO慢的超乎你的想象
- RabbitMQ之Helloworld
- Interesting article sharing: what is the difference between C language and C + +, C?
猜你喜欢

SQL 速查
这几个C++的坑,一旦踩中了,加班是肯定避免不了了!
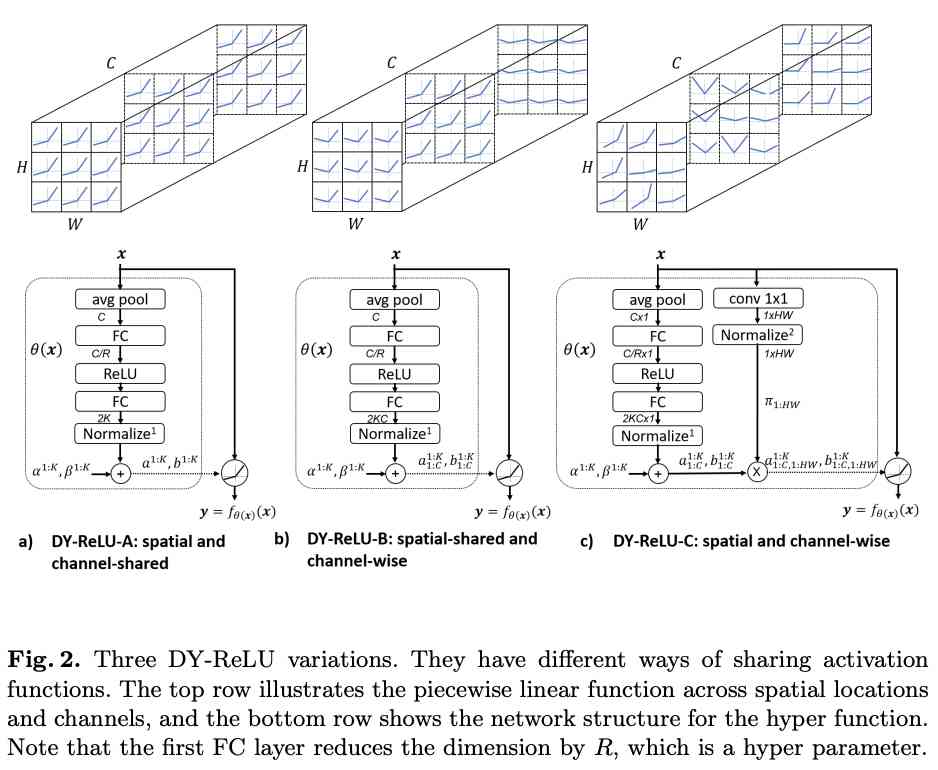
Dynamic ReLU:微软推出提点神器,可能是最好的ReLU改进 | ECCV 2020

PHP生成唯一字符串
Tencent: Although Ali's Taichung is good, it is not omnipotent!
vim-配置教程+源码

Awk implements SQL like join operation
Interesting article sharing: what is the difference between C language and C + +, C?

函数分类大pk!sigmoid和softmax,到底分别怎么用?
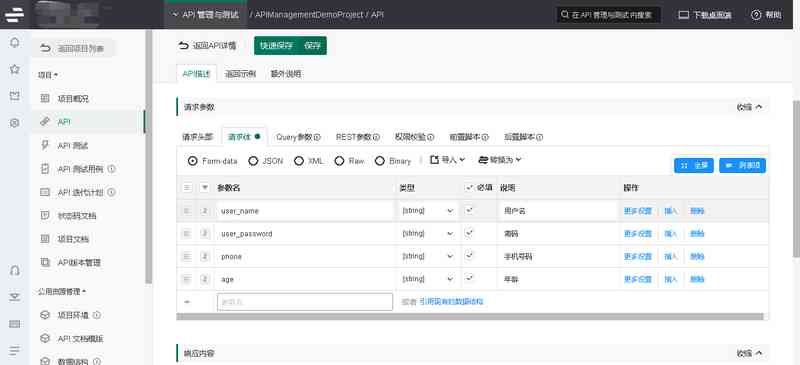
接口测试用例思路总结
随机推荐
如何将PyTorch Lightning模型部署到生产中
awk实现类sql的join操作
PHP生成唯一字符串
搭载固态硬盘的服务器究竟比机械硬盘快多少
AI香水来了,你会买吗?
Learn to record and analyze
线程池运用不当的一次线上事故
学习记录并且简单分析
Js中常见的内存泄漏场景
前后端分离跨域问题解决方案
Liteos message queuing
experiment
学习记录并且简单分析
How to make a correct summary for 7 years?
How much disk IO does a byte of read file actually take place?
关于update操作并发问题
go语言参数传递到底是传值还是传引用?
Introduction to latex
Talking about, check the history of which famous computer viruses, 80% of the people do not know!
Gopherchina 2020 Conference