2. Preliminary exercises of C language (2)

Catalog

TEXT 1 （ Sum of arithmetic sequence ）

TEXT 2 （ Print prime numbers ）

TEXT 3 （ Find the greatest common divisor ）

TEXT 4 （ Print 1000~2000 Leap year between ）

TEXT 5 （ Seeking growth rate ）

TEXT 6 （ Print in reverse order ）

TEXT 7 （ The scope of the round tower ）

TEXT 8 （ seek 1！+2！+...+n！）

TEXT 9 （ Find the perfect number ）

TEXT 10（ Count the daffodils （ Iteration and recursion ））

---

TEXT 1 （ Sum of arithmetic sequence ）

Calculation 1+2+3+...+100 Combination of

#include<stdio.h>

int main()
{
	int i = 0;
	int sum = 0;
	for (i = 1; i <= 100; i++)
	{
		sum += i;
	}
	printf("%d\n", sum);
	return 0;
}

here sum+=i And sum=sum+i Means exactly the same , Expressed as a variable i Value added to sum On .

TEXT 2 （ Print prime numbers ）

Print 100~200 All the prime Numbers between

#include<math.h>
#include<stdio.h>

int main()
{
	int i = 0;
	int j = 0;
	for (i = 100; i <= 200; i++)
	{
		int num = 0;// Count , Zero at the beginning of each cycle 
		for (j = 2; j <= sqrt(i); j++)
		{
			if (i % j == 0)
			{
				num++;
			}
		}
		if (num == 0)
		{
			printf("%d\n", i);
		}
	}
	return 0;
}

If a number x Non prime number , Then there must be （ One of the factors ）<=（x Square root ）.

for example ：16, form 16 There are three possibilities ：1 and 16、2 and 8、4 and 4, here 1、2、4 All less than or equal to 16 Square root , That is to say 4; When 16 Can be 1、2、4 Divisible time , Will also be able to 16、8 and 4 to be divisible by . So when writing code to find factors , Just find its square root to stop .

sqrt For square root , The general format is sqrt(), The header file is <math.h>, The return value is double type , You can use integer variables to receive sqrt The return value of .

TEXT 3 （ Find the greatest common divisor ）

Enter two positive integers , Find the greatest common divisor .

#include<stdio.h>
int main()
{
	int a = 0, b = 0;
	scanf("%d%d", &a, &b);
	if (a < b)// Give a large number to a, Decimal to b
	{
		int i = a;
		a = b;
		b = i;
	}
	while (1)
	{
		int c = 0;
		if (a % b != 0)
		{
			c = b;
			b = a % b;
			a = b;
		}
		else
		{
			printf("%d\n", b);
			break;
		}
	}
	return 0;
}

The greatest common divisor can be obtained fastest by using the rolling division method , here while(1) Set to dead loop , When finding the greatest common divisor break Out of the loop , Any two positive integers have common divisors 1, Don't worry about dead cycles .

Introduce the rolling division ： For example, o 40 and 14 Maximum common divisor of

Be careful ： The rolling division must be a large number divided by a decimal ！ So after entering two numbers , Judge , Assign a large number to a, A small number is assigned to b.

TEXT 4 （ Print 1000~2000 Leap year between ）

Print 1000~2000 Leap year between years

#include<stdio.h>
int main()
{
	int year = 0;
	int count = 0;
	for (year = 1000; year <= 2000; year += 4)
	{
		if ((year % 4 == 0 && year % 100 != 0) || year % 400 == 0)
		{
			printf("%d ", year);
			count++;
		}
	}
	printf("\n1000 Year to 2000 Between years %d Leap years \n", count);//243
	return 0;
}

Leap year ： A leap in four years , A hundred years without Leap , A leap in four hundred years .

use count Count , Print every leap year +1, At last, it comes to 1000~2000 Between years 243 Leap years .

because year stay for The loop is initialized to 1000,1000 Be able to divide 4, So after each cycle year+=4, This can greatly reduce the number of cycles .

TEXT 5 （ Seeking growth rate ）

Suppose the annual growth rate of China's gross national product is r=9%, Calculation n=10 The gross national product of our country will be higher than that of now , What percentage increase . Formula for ：.

#include<math.h>
#include<stdio.h>
int main()
{
	int n = 10;
	double r = 0.09;
	double p = pow((1+r), n);
	printf(" The percentage increase after ten years is %.0lf%%\n", p*100);
	return 0;
}

Finding the power requires a function pow,pow The general format of the function is pow(a,b), here a Base number ,b Is the index . Use pow The function needs to contain a header file <math.h>. Because it's a percentage , You need to print p*100, And omit the decimal part .

TEXT 6 （ Print in reverse order ）

Given integer , Print it in reverse order .

#include<stdio.h>

int main()
{
	int num = 12345678;
	while (1)
	{
		if (num / 10 != 0)
		{
			printf("%d", num % 10);
			num=num/10;
		}
		else
		{
			printf("%d", num);
			break;
		}
	}
	return 0;
}

How to get the last number ？（ for example 124）

• First cycle ：124%10=4, take 4 Print ,124/10=12;
• The second cycle ：12%10=2, take 2 Print ,1/10=0;
• Last ：0%10=0, Get into else, Print 1,break Out of the loop ;
• What is displayed on the screen is 421 了 .

TEXT 7 （ The scope of the round tower ）

4 A radius is 1 Round tower of , The coordinates of the center of the circle are ：（2,2）、（-2,2）、（-2,-2）、（2,-2）. Except for the round tower , The rest are vacant . Now enter the coordinates x、y, Judge whether the point is in the round tower （ Include boundary ）.

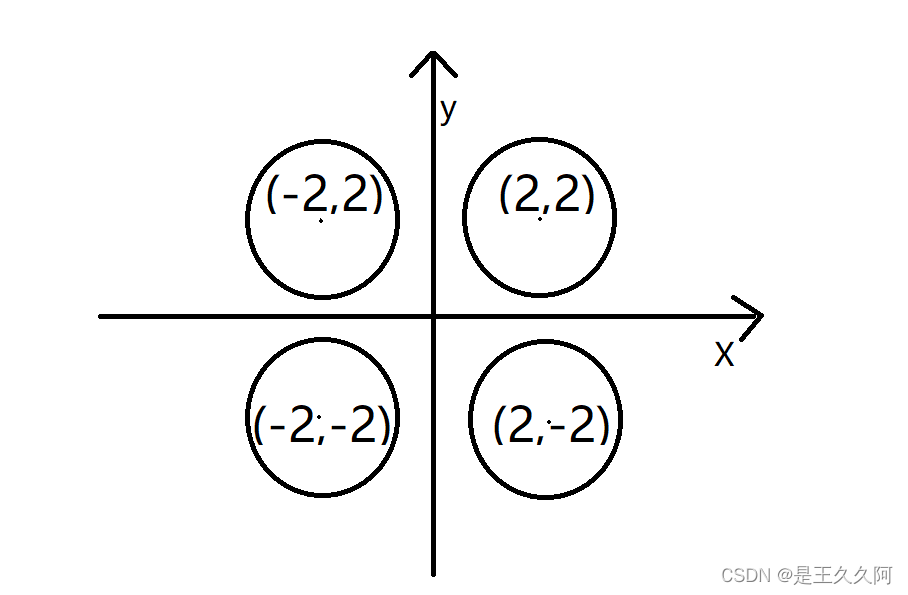
#include<stdio.h>
#include<math.h>

int main()
{
	double x = 0.0, y = 0.0;
	scanf("%lf%lf", &x, &y);
	double d1 = sqrt(pow((x - 2), 2) + pow((y - 2), 2));
	double d2 = sqrt(pow((x + 2), 2) + pow((y - 2), 2));
	double d3 = sqrt(pow((x + 2), 2) + pow((y + 2), 2));
	double d4 = sqrt(pow((x - 2), 2) + pow((y + 2), 2));
	if (d1 > 1 && d2 > 1 && d3 > 1 && d4 > 1)
	{
		printf(" This point is on the open space \n");
	}
	else
	{
		printf(" This point is on the round tower \n");

	}
	return 0;
}

Calculation point （x、y） The distance to the center of four circles （sqrt and pow It says , Remember to include header files <math.h>）, If all four distances are greater than 1（ The radius of the circle ）, Then it should be on the open space , Otherwise, it will be on the round tower .

TEXT 8 （ seek 1！+2！+...+n！）

Enter a positive integer n, seek 1！+2！+...+n！ Combination of .

#include<stdio.h>

int main()
{
	int n = 0;
	scanf("%d", &n);
	int i = 0;
	int j = 0;
	int sum = 0;
	for (i = 1; i <= n; i++)
	{
		int ret = 1;// Every reset ret=1
		for (j = 1; j <= i; j++)
		{
			ret *= j;
		}
		sum += ret;
	}
	printf("%d\n", sum);
	return 0;
}

For o 1！+2！+...+n！, First of all, we must be able to ask n！ How much is the .

// seek n！

#include<stdio.h>

int n = 0;
int j = 0;
int ret = 1;
scanf("%d",&n);

     for (j = 1; j <= n; j++)
		{
			ret *= j;
		}

The above part of the code is for n！ The factorial , Then put it in for In circulation , Accumulate the results of each factorial .

Note here ,ret For every time n The counting variable in the factorial of , When the factorial is completed , Reset the factorial of the next number to 1, otherwise ret Historical data will be preserved , The result is bigger and bigger .

TEXT 9 （ Find the perfect number ）

If a number is equal to the sum of its factors , This number is called the perfect number .

for example ：6 The factor is 1、2、3,1+2+3=6, therefore 6 The number is perfect. .（ The factor is all the numbers that can divide this number , But not the number itself ）

seek 1000 All the completions within , And output in the following format ：

6 The number is perfect. , Its factor is :1 2 3

#include<stdio.h>

int main()
{
	int i = 0;
	int j = 0;
	for (i = 1; i < 1000; i++)
	{
		int sum = 0;
		int k = 0;
		int arr[50] = { 0 };// Storage factor 
		for (j = 1; j < i; j++)// Judge the completion part 
		{
			if (i % j == 0)
			{
				sum += j;
				arr[k++] = j;// After ++, First use , Again ++
			}
		}
		if (sum == i)
		{
			printf("%d The number is perfect. , Its factor is :", i);
			for(k=0;arr[k]!='\0';k++)// Traverse the print factor 
			{
				printf("%d ", arr[k]);
		    }
			putchar('\n');
		}
	}
}

Create a arr To store the factors , Because of the demand 1000 Within the end of , So here arr The space should not be too small , Leave enough space for storing factors . With two for Cycle to judge the completion , Then print out the complete factor traversal .

TEXT 10（ Count the daffodils （ Iteration and recursion ））

Count all daffodils , The Narcissus count is a three digit number , The sum of the cubes of each number is equal to itself .

for example ：, so 153 It's Narcissus .

Iterative method ：

#include<stdio.h>
#include<math.h>

int main()
{
	int i = 0;
	int j = 0;
	for (i = 100; i < 1000; i++)
	{
		int ret = i;
		int sum = 0;
		for(j = 1; j <= 3; j++)// Find the cubic sum of each digit 
		{
			sum += (int)pow((ret%10), 3);//（int） Cast to type 
			ret = ret / 10;
		}
		if (sum == i)// The sum of cubes is equal to itself , Is the number of daffodils 
		{
			printf("%d It's Narcissus \n", i);//153 370 371 407
		}
	}
	return 0;
}

Because the number of daffodils is three digits , So in the big cycle ,i The range of is set to 100 <= i < 1000.

Then start every time i The sum of the cubes of the numbers ： In order not to change i Value , Create a ret Variable , take i Value is assigned to ret, At the end of each cycle , Will give ret new i value .

The idea here is similar to TEXT 6 The reverse order printing of is somewhat similar , Find the last digit every time , Find the cube sum , use sum recorded , After recording ret/10. The first cycle finds the cubic sum of single digits , The second cycle finds the cube sum of ten digits , The third cycle finds the cubic sum of hundreds , because i It's three digits , So you only need to cycle three times .

sum += (int)pow((ret%10), 3), here （int） Cast to type , take pow Of double The return value of type is converted to integer , Give Way sum receive .（ Of course , Even if not converted in VS The compiler can also run successfully ）

From the above code, we can observe , In the whole function , We created two local variables to store the results of our process , The whole code is very jumbled , Using recursive methods can simplify our code .

Recursive method ：

#include<stdio.h>
#include<math.h>

int flo(int i)
{
	int sum = 0;
	if (i / 10 != 0)
	{
		sum = flo(i / 10);
	}
	return sum += pow((i % 10), 3);
}

int main()
{
	int i = 0;
	for (i = 100; i < 1000; i++)
	{
		if (flo(i) == i)
		{
			printf("%d It's Narcissus \n", i);
		}
	}
	return 0;
}

The idea of recursion is a little abstract , Here is a picture to show a better understanding .

for example ： seek 125 Your cube

• First ,125 It can be divided into 12 and 5, seek 5 The cube of + seek 12 Your cube
• secondly ,12 It can be divided into 2 and 5, seek 2 The cube of + seek 1 Your cube
• Last ,1 Just itself , seek 1 The cube of .

The following is the flow chart of recursive call ：

return sum += pow((i % 10), 3); It can be understood as ：

1、sum += pow((i % 10), 3);

2、return sum;

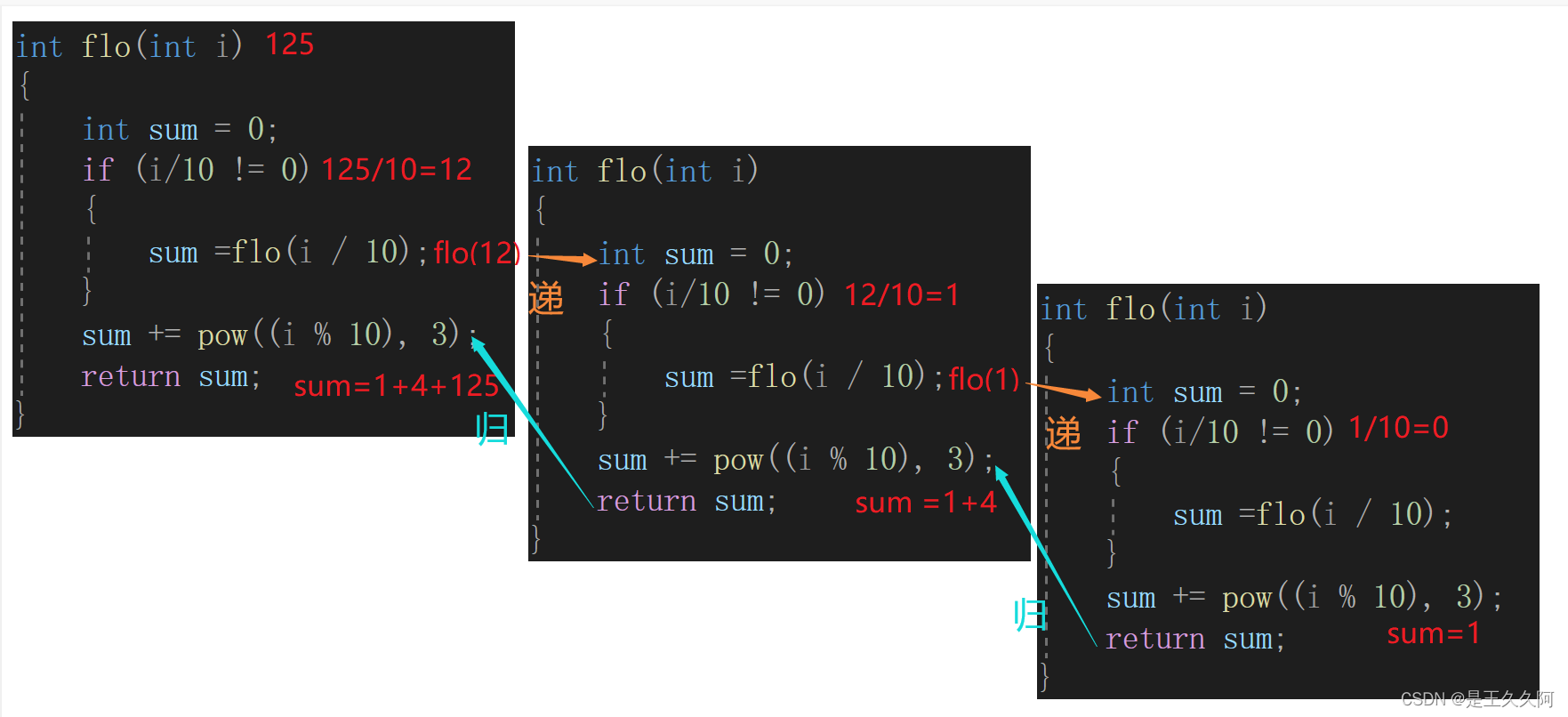
recursive ： Is to use functions to call themselves , So as to realize the simplification , Make a big deal small .

Recursion is mainly divided into recursion 、 And return to two parts , Hand it over before returning .

Every time I recurs , Get closer if Bounds in expressions , If there is no boundary , Then infinite recursion , Fall into a dead cycle .

for example 125 Recursive time , When 1/10=0 when , Expression is false , No longer call functions , Start with the next statement , Calculation sum Value , then return To the previous recursion , Until all return End , Recursion ends .