当前位置:网站首页>LeetCode practice and self-comprehension record (1)
LeetCode practice and self-comprehension record (1)
2022-08-05 06:33:00 【monkeyhlj】
文章目录
LeetCodePractice and understand the records yourself(1)
516. 最长回文子序列
来源:https://leetcode-cn.com/problems/longest-palindromic-subsequence/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-dpzi-dv83q/
1、确定dp数组以及其下标的含义
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j].
2、确定递推公式
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
Because the same words exist in the subsequence2个数字,也就是2个长度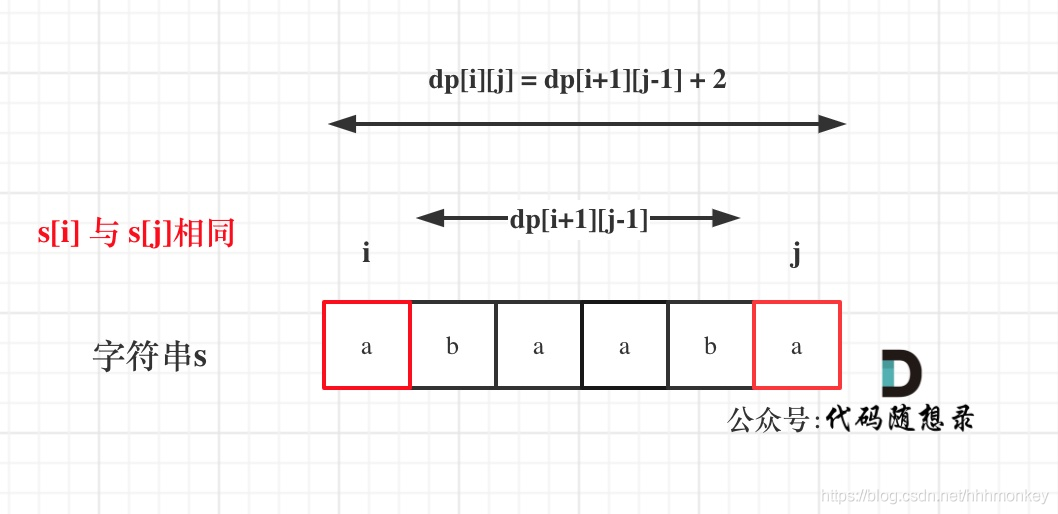
如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入并不能增加[i,j]区间回文子串的长度,那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列.
加入s[j]的回文子序列长度为dp[i + 1][j].
加入s[i]的回文子序列长度为dp[i][j - 1].
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);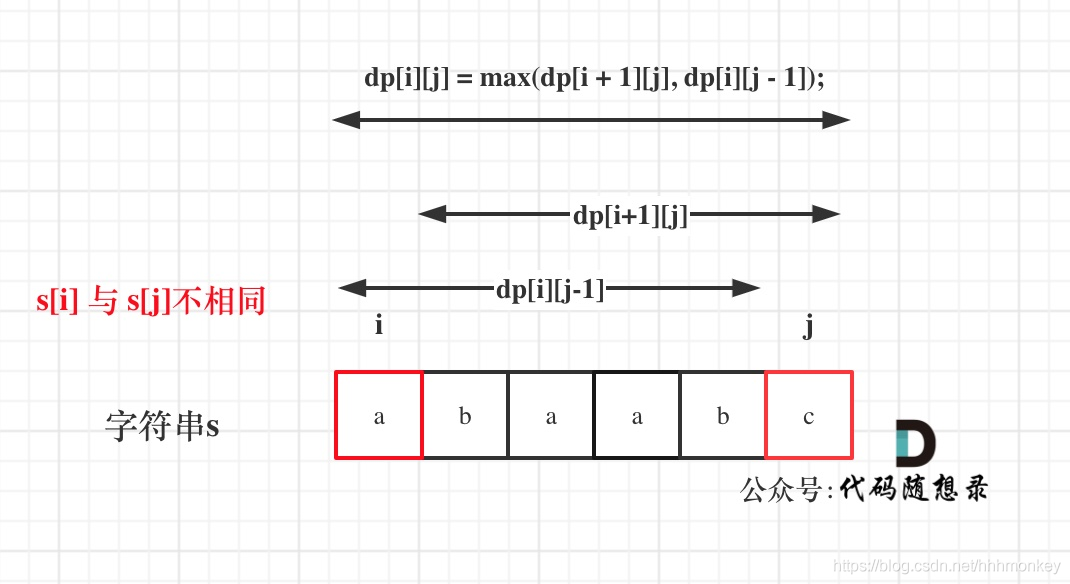
3、dp数组如何初始化
首先要考虑当i 和j 相同的情况,从递推公式:dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况.
所以需要手动初始化一下,当i与j相同,那么dp[i][j]一定是等于1的,即:一个字符的回文子序列长度就是1.
其他情况dp[i][j]初始为0就行,这样递推公式:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); 中dp[i][j]才不会被初始值覆盖.
4、确定遍历顺序
从递推公式dp[i][j] = dp[i + 1][j - 1] + 2 和 dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]) 可以看出,dp[i][j]是依赖于dp[i + 1][j - 1] 和 dp[i + 1][j],
也就是从矩阵的角度来说,dp[i][j] 下一行的数据. 所以遍历i的时候一定要从下到上遍历,这样才能保证,下一行的数据是经过计算的.
递推公式:dp[i][j] = dp[i + 1][j - 1] + 2,dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]) 分别对应着下图中的红色箭头方向,如图: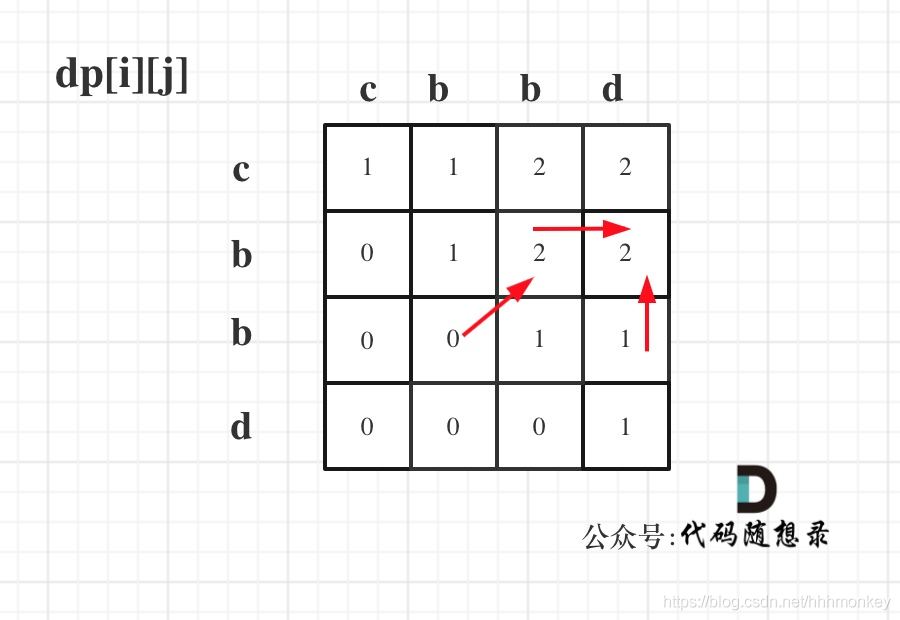
5、举例推导dp数组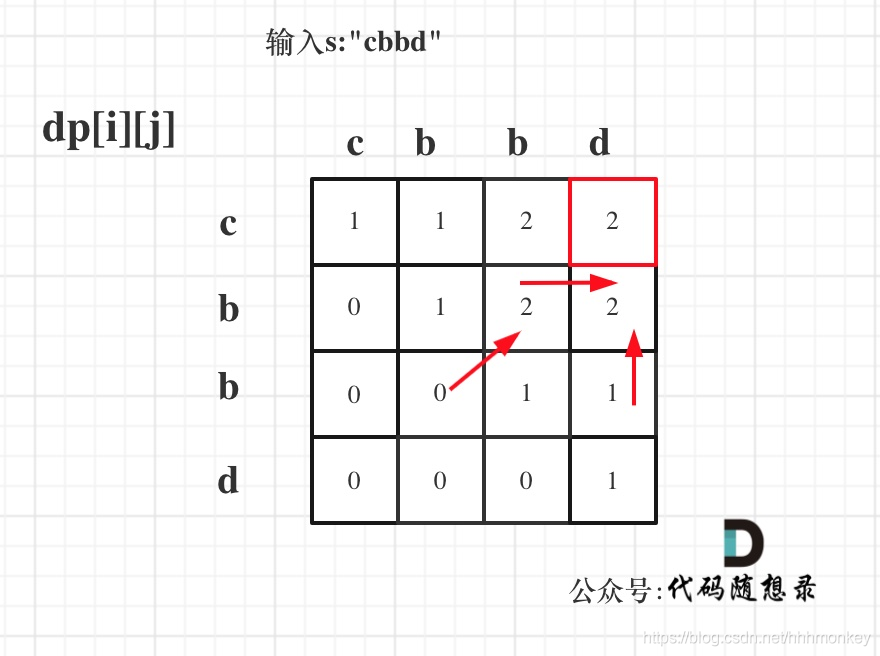
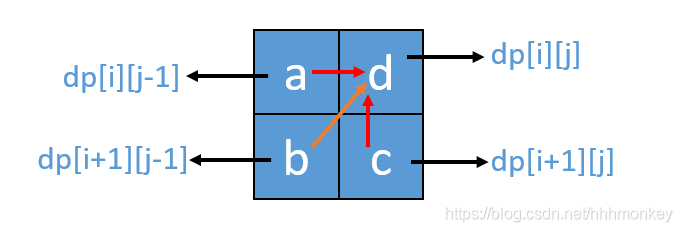
If you don't understand the above process, you can look at it in conjunction with the graph of the field character grid above,A process to see where the arrows flow,You should be able to understand the entire dynamic programming process.
class Solution {
public int longestPalindromeSubseq(String s) {
int n = s.length();
int dp[][] = new int[n][n];
for(int i=n-1;i>=0;i--){
dp[i][i]=1;
char a=s.charAt(i);
for(int j=i+1;j<n;j++){
char b=s.charAt(j);
if(a==b){
dp[i][j]=dp[i+1][j-1]+2;
}else{
dp[i][j]=Math.max(dp[i][j-1],dp[i+1][j]);
}
}
}
return dp[0][n-1];
}
}
class Solution(object):
def longestPalindromeSubseq(self, s):
""" :type s: str :rtype: int """
n = len(s)
dp = [[0] * n for i in range(n)]
for i in range(n-1,-1,-1):
dp[i][i]=1
for j in range(i+1,n):
if s[i]==s[j]:
dp[i][j] = dp[i+1][j-1]+2
else:
dp[i][j] = max(dp[i+1][j],dp[i][j-1])
return dp[0][n-1]
/** * @param {string} s * @return {number} */
var longestPalindromeSubseq = function(s) {
var n = s.length;
var dp = new Array(n).fill(0).map(()=>new Array(n).fill(0));
for(var i=n-1;i>=0;i--){
dp[i][i] = 1;
var a = s.charAt(i);
for(var j=i+1;j<n;j++){
var b = s.charAt(j);
if(a==b){
dp[i][j] = dp[i+1][j-1]+2;
}else{
dp[i][j] = Math.max(dp[i][j-1],dp[i+1][j]);
}
}
}
return dp[0][n-1];
};
链接: https://pan.baidu.com/s/1E08ocgXThceqWEddOICoyg 密码: ts8t I recommend his articles on dynamic programming.
148. 排序链表
/** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode() {} * ListNode(int val) { this.val = val; } * ListNode(int val, ListNode next) { this.val = val; this.next = next; } * } */
class Solution {
public ListNode sortList(ListNode head) {
return mergeSort(head,null);
}
public ListNode mergeSort(ListNode head,ListNode tail){
if(head == null){
return head;
}
if (head.next == tail) {
//It was just ignored here
head.next = null;
return head;
}
//找出中点
ListNode slow = head, fast = head;
while (fast != tail) {
slow = slow.next;
fast = fast.next;
if (fast != tail) {
fast = fast.next;
}
}
ListNode mid = slow;
ListNode l1=mergeSort(head,mid);
ListNode l2=mergeSort(mid,tail);
ListNode sorted = merge(l1,l2);
return sorted;
}
public ListNode merge(ListNode head1,ListNode head2){
ListNode dumpHead = new ListNode(0);
ListNode temp=dumpHead,temp1=head1,temp2=head2;
while(temp1 != null && temp2 != null){
if(temp1.val <= temp2.val){
temp.next = temp1;
temp1 = temp1.next;
}else{
temp.next = temp2;
temp2 = temp2.next;
}
temp = temp.next;
}
if (temp1 != null) {
temp.next = temp1;
} else if (temp2 != null) {
temp.next = temp2;
}
return dumpHead.next;
}
}
采用归并排序(递归)的方式,It's just the first time that this way of finding the midpoint of the node is used(快慢指针),Even numbers are after the midpoint,The odd number is the midpoint,The point ignored above is the key,否则会陷入死循环.Merging is to compare the size of the values of two nodes,Finally, the head node of the ordered linked list is returned.
56. 合并区间
class Solution {
public int[][] merge(int[][] intervals) {
if(intervals.length < 2){
return intervals;
}
Arrays.sort(intervals, new Comparator<int[]>() {
//新知识
public int compare(int[] a, int[] b) {
if(a[0] == b[0]) {
return a[1] - b[1];
}
return a[0] - b[0];
}
});
List<int[]> result = new ArrayList<int[]>();
for(int i=0;i<=intervals.length-1;i++){
int L = intervals[i][0],R = intervals[i][1];
if(result.size() == 0 || result.get(result.size()-1)[1] < L){
result.add(intervals[i]);
}else{
result.get(result.size()-1)[1] = Math.max(result.get(result.size()-1)[1], R);
}
}
return result.toArray(new int[result.size()][]);
}
}
The above is used directlyArrays对二维数组排序,重写Comparator方法(第一次用,学到了),Then compare the sorted ones[L,R],Added to by comparisonArrayList中,So don't start building two-dimensional arrays directly,To create a linked list,因为数组的大小是固定的.
57. 插入区间
class Solution {
public int[][] insert(int[][] intervals, int[] newInterval) {
List<int[]> list = new ArrayList<int[]>();
List<int[]> result = new ArrayList<int[]>();
for(int i=0;i<intervals.length;i++){
list.add(intervals[i]);
}
list.add(newInterval);
int[][] arr = list.toArray(new int[list.size()][]);
Arrays.sort(arr,new Comparator<int[]>() {
public int compare(int[] a,int[] b) {
return a[0]-b[0];
}
});
for(int i=0;i<arr.length;i++){
int L = arr[i][0],R = arr[i][1];
if(result.size() == 0 || result.get(result.size()-1)[1] < L){
result.add(arr[i]);
}else{
result.get(result.size()-1)[1] = Math.max(result.get(result.size()-1)[1], R);
}
}
return result.toArray(new int[result.size()][]);
}
}
以上是在56improved on topic,But not optimal,You can see better in the solution later:
class Solution {
public int[][] insert(int[][] intervals, int[] newInterval) {
int left = newInterval[0];
int right = newInterval[1];
boolean placed = false;
List<int[]> ansList = new ArrayList<int[]>();
for (int[] interval : intervals) {
if (interval[0] > right) {
// 在插入区间的右侧且无交集
if (!placed) {
ansList.add(new int[]{
left, right});
placed = true;
}
ansList.add(interval);
} else if (interval[1] < left) {
// 在插入区间的左侧且无交集
ansList.add(interval);
} else {
// 与插入区间有交集,计算它们的并集
left = Math.min(left, interval[0]);
right = Math.max(right, interval[1]);
}
}
if (!placed) {
ansList.add(new int[]{
left, right});
}
int[][] ans = new int[ansList.size()][2];
for (int i = 0; i < ansList.size(); ++i) {
ans[i] = ansList.get(i);
}
return ans;
}
}
102. 二叉树的层序遍历
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> list = new ArrayList<>();
if(root == null) return list;
List<Integer> temp = new ArrayList<>();
temp.add(root.val);
list.add(temp);
Queue<TreeNode> queue = new LinkedList<>();
Queue<TreeNode> queueTemp = new LinkedList<>();
queue.offer(root);
int levelSize = 1;
while(!queue.isEmpty()){
TreeNode node = queue.poll();
levelSize--;
if(node.left != null){
queue.offer(node.left);
queueTemp.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
queueTemp.offer(node.right);
}
if(levelSize == 0){
levelSize = queue.size();
List<Integer> temp2 = new ArrayList<>();
while(!queueTemp.isEmpty()){
TreeNode nodeTemp = queueTemp.poll();
temp2.add(nodeTemp.val);
}
if(!temp2.isEmpty()){
list.add(temp2);
}
}
}
return list;
}
}
107. 二叉树的层序遍历 II
class Solution {
public List<List<Integer>> levelOrderBottom(TreeNode root) {
List<List<Integer>> list = new ArrayList<>();
if(root == null) return list;
List<Integer> temp = new ArrayList<>();
temp.add(root.val);
list.add(0,temp); //getto a new method
Queue<TreeNode> queue = new LinkedList<>();
Queue<TreeNode> queueTemp = new LinkedList<>();
queue.offer(root);
int levelSize = 1;
while(!queue.isEmpty()){
TreeNode node = queue.poll();
levelSize--;
if(node.left != null){
queue.offer(node.left);
queueTemp.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
queueTemp.offer(node.right);
}
if(levelSize == 0){
levelSize = queue.size();
List<Integer> temp2 = new ArrayList<>();
while(!queueTemp.isEmpty()){
TreeNode nodeTemp = queueTemp.poll();
temp2.add(nodeTemp.val);
}
if(!temp2.isEmpty()){
list.add(0,temp2);
}
}
}
return list;
}
}
662. 二叉树最大宽度
A two-way queue is used.才可有getFirst()和getLsat()方法
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */
class Solution {
public int widthOfBinaryTree(TreeNode root) {
if(root == null) return 0;
// Queue<TreeNode> queue = new LinkedList<>();
Deque<TreeNode> queue = new ArrayDeque<>();//A two-way queue is required
root.val = 0;
queue.offer(root);
int res = 0;
while(!queue.isEmpty()){
int size = queue.size();
res = Math.max(res,queue.getLast().val-queue.getFirst().val+1);
for(int i=0;i<size;i++){
TreeNode node = queue.poll();
if(node.left != null){
node.left.val = 2*node.val;
queue.offer(node.left);
}
if(node.right != null){
node.right.val = 2*node.val+1;
queue.offer(node.right);
}
}
}
return res;
}
}
559. N 叉树的最大深度
/* // Definition for a Node. class Node { public int val; public List<Node> children; public Node() {} public Node(int _val) { val = _val; } public Node(int _val, List<Node> _children) { val = _val; children = _children; } }; */
class Solution {
public int maxDepth(Node root) {
if(root == null) return 0;
Queue<Node> queue = new LinkedList<>();
queue.offer(root);
int height = 0;
int levelSize = 1;
int sizetemp = 0;
while(!queue.isEmpty()){
Node node = queue.poll();
levelSize--;
for(int i=0;i<node.children.size();i++){
if(node.children.get(i) != null){
queue.offer(node.children.get(i));
sizetemp++; //Record the number of each layer
}
}
if(levelSize == 0){
height++;
levelSize = sizetemp; //重新赋值
sizetemp = 0; //重新置为0
}
}
return height;
}
}
The above are my thoughts,It is not the same as the method of solving the problem,But the operating efficiency is a little worse.
889. 根据前序和后序遍历构造二叉树
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */
class Solution {
public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
if(preorder == null || preorder.length == 0){
return null;
}
return dfs(preorder,postorder);
}
public TreeNode dfs(int[] preorder, int[] postorder){
if(preorder == null || preorder.length == 0){
return null;
}
//数组长度为1时,直接返回即可!!!!!!
if(preorder.length==1) {
return new TreeNode(preorder[0]);
}
TreeNode root = new TreeNode(preorder[0]);
int n = preorder.length;
for(int i=0;i<postorder.length;i++){
if(preorder[1] == postorder[i]){
int line = i+1;
int[] pre_left = Arrays.copyOfRange(preorder,1,line+1);
int[] pre_right = Arrays.copyOfRange(preorder,line+1,n);
int[] post_left = Arrays.copyOfRange(postorder,0,line);
int[] post_right = Arrays.copyOfRange(postorder,line,n-1);
root.left = dfs(pre_left,post_left);
root.right = dfs(pre_right,post_right);
break;
}
}
return root;
}
}
450. 删除二叉搜索树中的节点
class Solution {
public int rightMin(TreeNode root) {
//1.找到以某个结点为根节点的右子树最小值.
root = root.right;
while (root.left != null) root = root.left;//1.1循环往左找到最大值.
return root.val;
}
public int leftMax(TreeNode root) {
//2.找到以某个结点为根节点的左子树最大值.
root = root.left;
while (root.right != null) root = root.right;
return root.val;
}
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) {
//3.递归终止条件
return null;
}
if (key > root.val) {
//4.如果查找的结点比根节点大,继续在右子树查找删除该结点
root.right = deleteNode(root.right, key);
} else if (key < root.val) {
//5.如果查找的结点比根节点小,继续在左子树查找删除该结点
root.left = deleteNode(root.left, key);
} else {
//6.如果找到了该结点,删除它
if (root.left == null && root.right == null) {
//7.以叶子节点为根节点的二叉搜索树只有一个元素,可以直接删除.
root = null;
} else if (root.right != null) {
//8.如果有右子树,只要找到该右子树的最小值来替换,之后将它删除即可.
root.val = rightMin(root);
root.right = deleteNode(root.right, root.val);//9.将这个右子树的最小值替换根节点,此时存在两个相同节点,将这个节点删除即可.
} else {
//10.如果有左子树,只要找到该左子树的最大值来替换,之后将它删除即可.
root.val = leftMax(root);
root.left = deleteNode(root.left, root.val);//9.将这个左子树的最大值替换根节点,此时存在两个相同节点,将这个节点删除即可.
}
}
return root;
}
}
1361. 验证二叉树
class Solution {
public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {
int[] findFather = new int[n]; //先找出入度为0的节点,即为root
for(int i=0;i<n;i++){
if(leftChild[i] != -1){
findFather[leftChild[i]]++;
}
if(rightChild[i] != -1){
findFather[rightChild[i]]++;
}
}
int root = -1;
int count = 0;
for(int i=0;i<n;i++){
if(findFather[i] == 0){
root = i;
count++;
}
if(findFather[i] == 2){
return false;
}
}
if(root == -1 || count > 1){
return false;
}
Queue<Integer> queue = new LinkedList<>();
List<Integer> list = new ArrayList<>(); //记录遍历的节点
queue.offer(root);
list.add(root);
while(!queue.isEmpty()){
int node = queue.poll();
if(leftChild[node] != -1){
if(list.contains(leftChild[node])){
return false;
}
list.add(leftChild[node]);
queue.offer(leftChild[node]);
}
if(rightChild[node] != -1){
if(list.contains(rightChild[node])){
return false;
}
list.add(rightChild[node]);
queue.offer(rightChild[node]);
}
}
return list.size() == n;
}
}
101. 对称二叉树
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root == null) return true;
return check(root.left,root.right); //递归检查
}
public boolean check(TreeNode p,TreeNode q){
if(p == null && q == null){
return true;
}
if(p == null || q == null){
return false;
}
return p.val == q.val && check(p.left,q.right) && check(p.right,q.left);
}
}
边栏推荐
- [问题已处理]-虚拟机报错contains a file system with errors check forced
- Quick question and quick answer - FAQ of Tencent Cloud Server
- 618,你也许可以清醒亿点点
- Hugo builds a personal blog
- DevOps process demo (practical record)
- Vim tutorial: vimtutor
- 从“双卡双待“到”双通“,vivo率先推动DSDA架构落地
- Seven Ways to Center a Box Horizontally and Vertically
- ALC实验
- D39_Vector
猜你喜欢
DevOps流程demo(实操记录)
What's the point of monitoring the involution of the system?
BIO,NIO,AIO实践学习笔记(便于理解理论)
The problem come from line screening process

LeetCode中常用语言的一些基本方法记录

The highlight moment of operation and maintenance starts with intelligence

el-autocomplete use
单臂路由实验和三层交换机实验

Technology Sharing Miscellaneous Technologies

Vim tutorial: vimtutor
随机推荐
Tencent Cloud Message Queue CMQ
NAT实验
VLAN介绍与实验
DevOps流程demo(实操记录)
Insight into the general trend of the Internet, after reading this article, you will have a thorough understanding of Chinese domain names
错误记录集锦(遇到则记下)
618,你也许可以清醒亿点点
Advantages of overseas servers
VRRP overview and experiment
DevOps-了解学习
Take you in-depth understanding of cookies
[issue resolved] - jenkins pipeline checkout timeout
Wireshark packet capture and common filtering methods
DevOps process demo (practical record)
通过反射获取Class对象的四种方式
RAID磁盘阵列
Next-Generation Parsing Technology - Cloud Parsing
Disk management and file systems
[ingress]-ingress exposes services using tcp port
input详解之文件上传