当前位置:网站首页>【4.6 中国剩余定理详解】
【4.6 中国剩余定理详解】
2022-07-26 22:38:00 【浪漫主义狗】
更好的阅读体验 \color{red}{更好的阅读体验} 更好的阅读体验
概念
若存在整数 m 1 , m 2 , m 3 … m n m_1,m_2,m_3\dots m_n m1,m2,m3…mn两两互质,则对于任意的整数 a 1 , a 2 , a 3 … a n a_1,a_2,a_3\dots a_n a1,a2,a3…an,一元线性同余方程组 ( S ) (S) (S)有通解
( S ) : { x ≡ a 1 ( m o d m 1 ) x ≡ a 2 ( m o d m 2 ) x ≡ a 3 ( m o d m 3 ) … x ≡ a n ( m o d m n ) (S): \begin{cases} x\equiv a_1(mod~m_1)\\ x\equiv a_2(mod~m_2)\\ x\equiv a_3(mod~m_3)\\ \dots\\ x\equiv a_n(mod~m_n)\\ \end{cases} (S):⎩⎨⎧x≡a1(mod m1)x≡a2(mod m2)x≡a3(mod m3)…x≡an(mod mn)
思想
对于 ( S ) (S) (S)其中的两个式子进行合并
{ x ≡ a 1 ( m o d m 1 ) x ≡ a 2 ( m o d m 2 ) ⇒ { x = k 1 m 1 + a 1 x = k 2 m 2 + a 2 \begin{cases} x\equiv a_1(mod~m_1)\\ x\equiv a_2(mod~m_2)\\ \end{cases} \Rightarrow \begin{cases} x=k_1m_1+a_1\\ x=k_2m_2+a_2\\ \end{cases} { x≡a1(mod m1)x≡a2(mod m2)⇒{ x=k1m1+a1x=k2m2+a2
将等价转换后的两式进行联立,化简得 k 1 m 1 + k 2 ( − m 2 ) = a 2 − a 1 ① k_1m_1+k_2(-m_2)=a_2-a_1~① k1m1+k2(−m2)=a2−a1 ①
由扩展欧几里得算法可以得到一组解 ( k 1 ′ , k 2 ′ ) ({k_1}',{k_2}') (k1′,k2′),使得: k 1 ′ m 1 + k 2 ′ ( − m 2 ) = g c d ( m 1 , − m 2 ) {k_1}'m_1+{k_2}'(-m_2)=gcd(m_1,-m_2) k1′m1+k2′(−m2)=gcd(m1,−m2)
若 g c d ( m 1 , − m 2 ) gcd(m_1,-m_2) gcd(m1,−m2)不能整除 a 2 − a 1 a2-a1 a2−a1,则无解,否则有通解
设 g c d ( m 1 , − m 2 ) = d , y = ( a 2 − a 1 ) d gcd(m_1,-m_2)=d,y=\frac{(a_2-a_1)}{d} gcd(m1,−m2)=d,y=d(a2−a1)
由扩展欧几里得算法的推论可知: { k 1 = k 1 ′ y k 2 = k 2 ′ y \begin{cases}k_1={k_1}'y\\k_2={k_2}'y\end{cases} { k1=k1′yk2=k2′y
引入通解 { k 1 = k 1 + k m 2 d k 2 = k 2 + m 1 d \begin{cases}k_1={k_1}+k\frac{m_2}{d}\\k_2={k_2}+\frac{m_1}d\end{cases} { k1=k1+kdm2k2=k2+dm1, k ∈ Z k\in \Z k∈Z
将通解带入 ① ① ①得 ( k 1 + k m 2 d ) m 1 + ( k 2 + k m 1 d ) ( − m 2 ) = a 2 − a 1 ({k_1}+k\frac{m_2}{d})m_1+({k_2}+k\frac{m_1}{d})(-m_2)=a_2-a_1 (k1+kdm2)m1+(k2+kdm1)(−m2)=a2−a1
化简得 k 1 m 1 + k 2 ( − m 2 ) = a 2 − a 1 k_1m_1+k_2(-m_2)=a_2-a_1 k1m1+k2(−m2)=a2−a1和 ① ① ①相同,故成立
重复上述步骤,不断合并剩余的式子,即可得到最终的通解
例题 表达整数的奇怪方式
描述
给定 2n 个整数 a1,a2,…,an 和 m1,m2,…,mn,求一个最小的非负整数 x,满足 ∀i∈[1,n],x≡mi(mod ai)。
输入格式
第 1 行包含整数 n。
第 2…n+1 行:每 i+1 行包含两个整数 ai 和 mi,数之间用空格隔开。
输出格式
输出最小非负整数 x,如果 x 不存在,则输出 −1。
如果存在 x,则数据保证 x 一定在 64 位整数范围内。
数据范围
1≤ai≤231−1,
0≤mi<ai
1≤n≤25
输入样例:
2
8 7
11 9
输出样例:
31
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
void exgcd(LL a,LL b, LL &x,LL &y){
if(!b){
x=1,y=0;
return ;
}
else{
exgcd(b,a%b,x,y);
LL t=x;
x=y;
y=t-a/b*y;
}
}
LL gcd(LL a,LL b){
return b ? gcd(b,a%b) : a;
}
int main(){
int n;
cin>>n;
LL x=0,m1,a1; //第一个方程的系数 备份数据
cin>>m1>>a1; //先输入第一个方程
for(int i=0;i<n-1;i++){
//合并接下来的n-1个方程
LL m2,a2;
cin>>m2>>a2;
LL k1,k2;
LL d=gcd(m1,m2);
exgcd(m1,m2,k1,k2);
if((a2-a1)%d){
//此时无解
x=-1;
break;
}
k1*=(a2-a1)/d;//特解
k1=(k1%(m2/d)+m2/d)%(m2/d); //让特解k1取到最小正整数解
x=k1*m1+a1;
LL m=abs(m1/d*m2);
a1=k1*m1+a1;
m1=m;
}
if(x!=-1) x=(a1%m1+m1)%m1 //当循环结束时,此时的值应该与最小公倍数取模,以求得最小正整数解
cout<<x<<endl;
return 0;
}
边栏推荐
- AutoCAD的卸载后重新安装,删除注册表的详细过程
- V-viewer use
- LeetCode——哈希表篇
- Knowledge distillation -- pytorch implementation
- C and pointer Chapter 18 runtime environment 18.7 problems
- Training team lpoj round10 e Jumping Frog
- 1、 Kubernetes basic concept + environment installation (build cross server public network environment)
- Leetcode - hash table
- 蒙着头配置deeplabcut 1
- "Could not load host key" error when xshell connects to the server
猜你喜欢

Matlab simulation of inverted pendulum control system based on qlearning reinforcement learning

Go exceed API source code reading (IV) -- save (), SaveAs (name string)

Today's 20220719 toss deeplobcut

画冲击函数
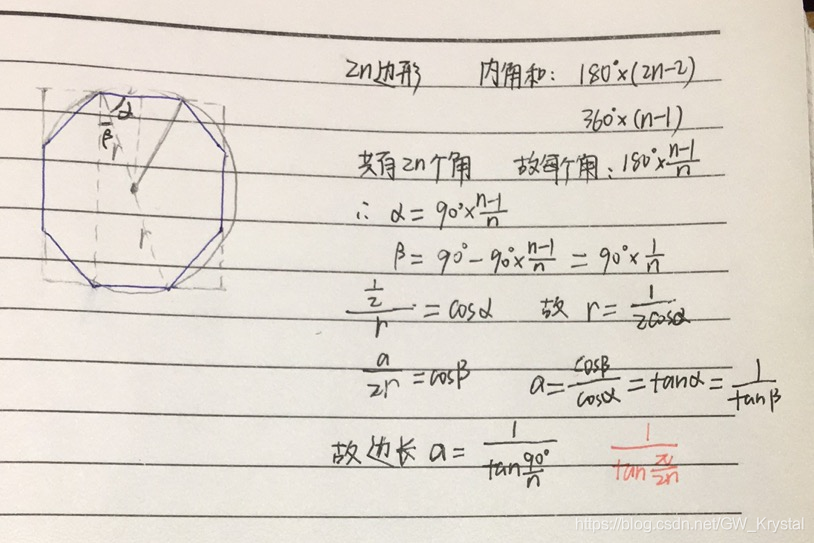
Codeforces C1. Simple Polygon Embedding

Deployment of yolov5 on Jetson nano deepstream

Request attribute in crawler

Leetcode high frequency question: the choice of the inn, how many options to choose accommodation, to ensure that you can find a coffee shop with a minimum consumption of no more than p yuan in the ev

10_评价分类结果(Evaluate classification)

6_梯度下降法(Gradient Descent)
随机推荐
类与对象笔记一
Oracle data guard service, process and protection mode
C and pointer Chapter 18 runtime environment 18.1 judgment of runtime environment
C and pointers Chapter 18 runtime environment 18.4 summary
Drawing warehouse-3 (functional image)
7_ Principal component analysis
Request attribute in crawler
知识蒸馏——pytorch实现
Signal and system impulse response and step response
Transpose convolution correlation
放图仓库-2(函数图像)
UNET notes
Complete review of parsing web pages
3_Jupyter Notebook, numpy和matplotlib
20220720折腾deeplabcut2
LeetCode——链表篇
C and pointer Chapter 18 runtime environment 18.2 interface between C and assembly language
Three tier architecture simulation
Collection of 3D LUT related articles
c语言 比大小的多种描述,不要只拘泥于一种写法