6_梯度下降法（Gradient Descent）

梯度下降法是在机器学习领域的一个重要的搜索策略。在这一章，我们将详细讲解梯度下降法的基本原理，一步一步改进梯度下降算法，让大家理解梯度下降法中各种参数，尤其是学习率的意义。
同时，我们还将引申出随机梯度下降法和小批量梯度下降法两个方法，让大家对梯度下降法家族有一个全方位的认识。…

6-1 什么是梯度下降法

• 导数代表 theta单位变化时,J相应的变化

• 导数可以代表方向,对应J增大的方向
  
  
  
  
  

  • 并不是所有函数都有唯一的极值点（多元多次函数）

6-3 线性回归中的梯度下降法

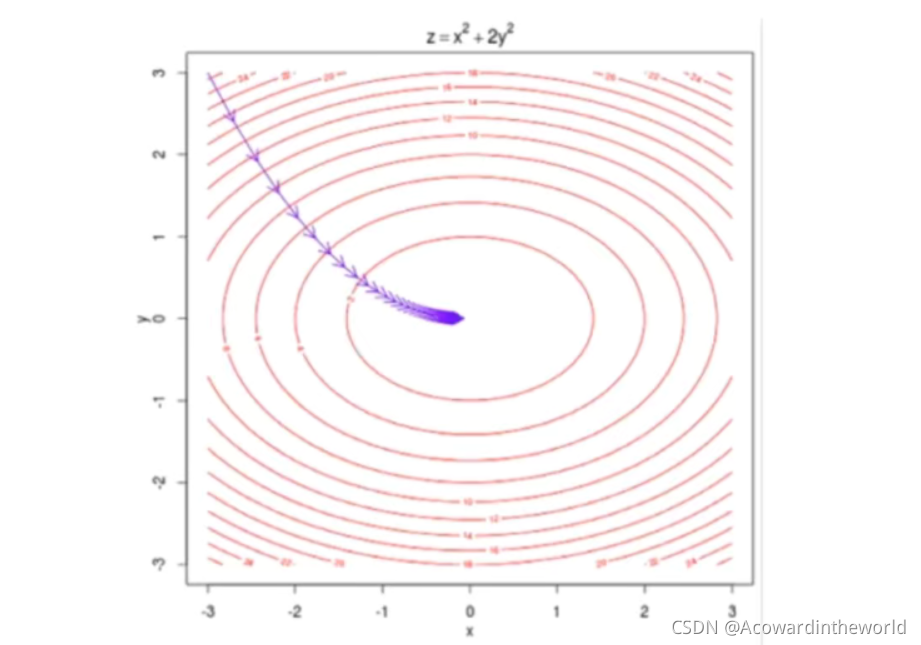
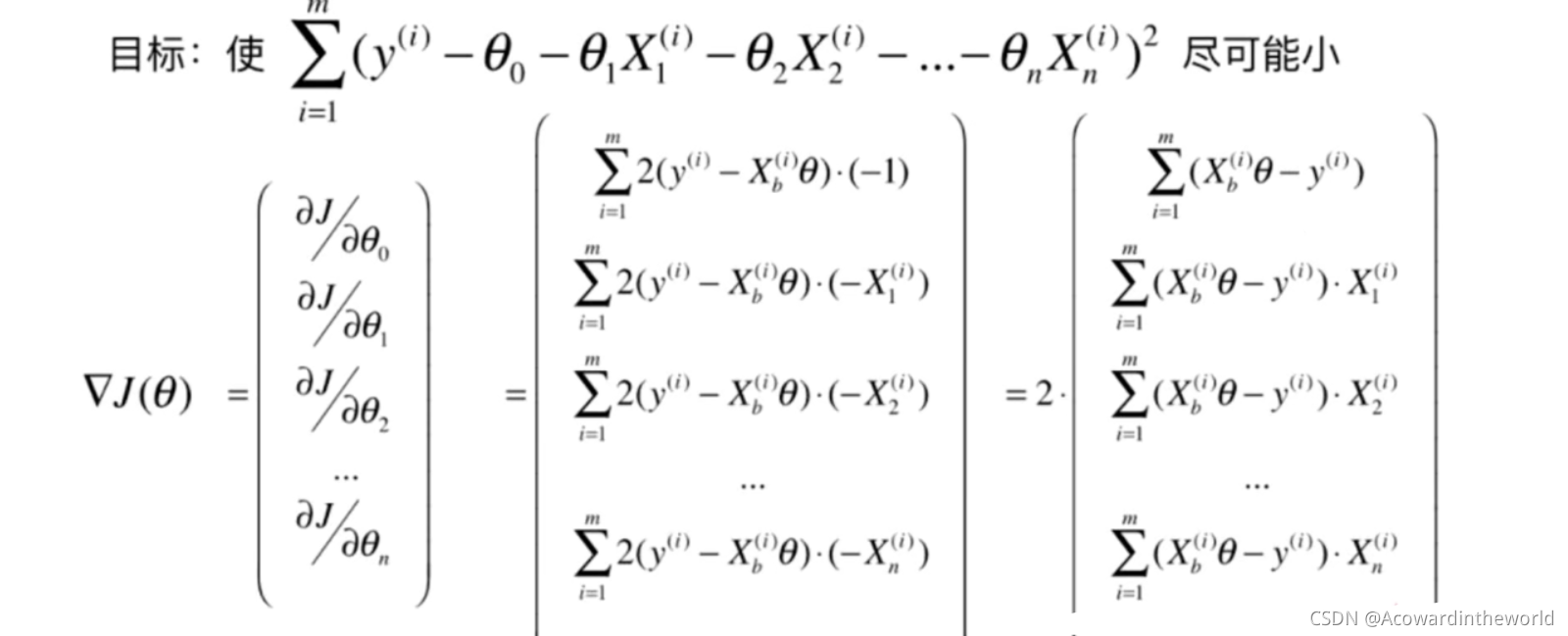
由于梯度的大小受样本数m影响，显然不合理，故除以样本数m，使其不受样本数量的影响。

6-4 实现线性回归中的梯度下降法

6-5 梯度下降法的向量化和数据标准化

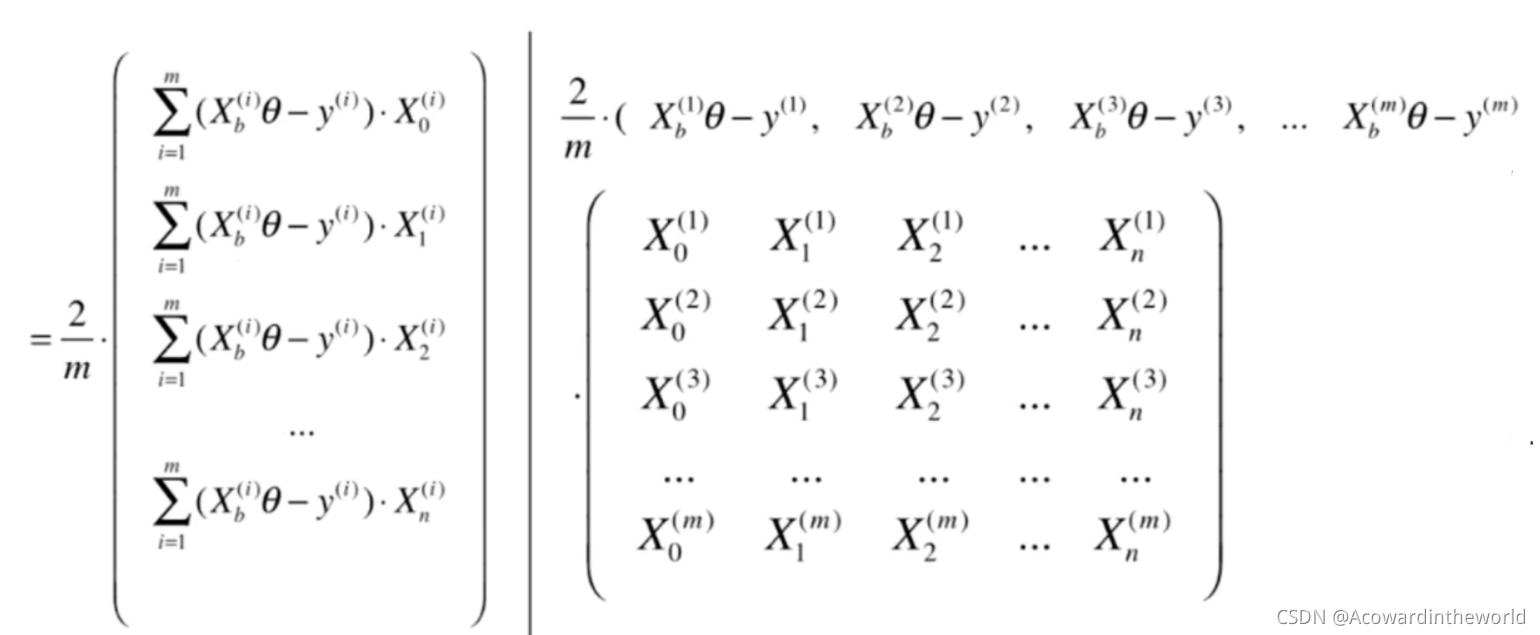
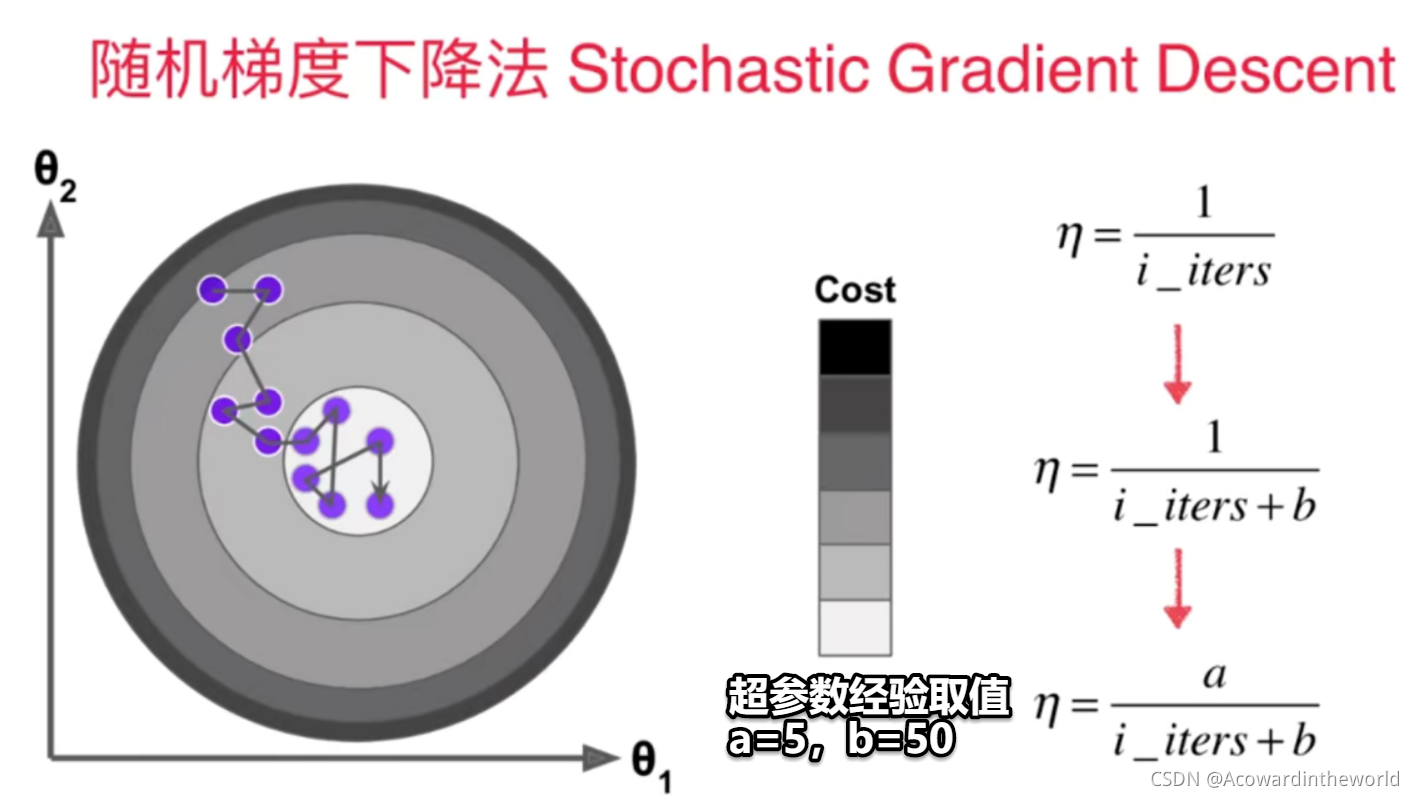
6-6 随机梯度下降法

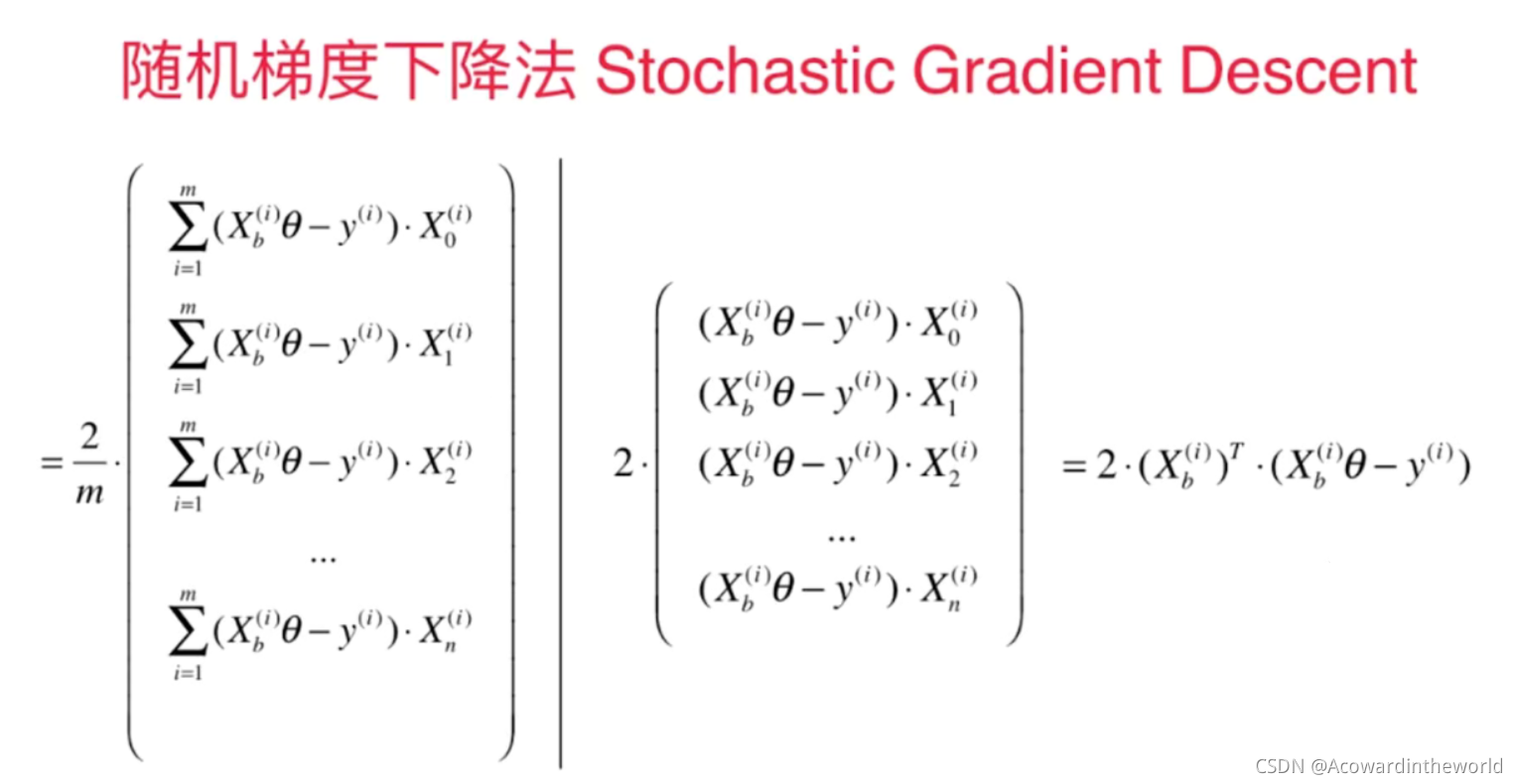
• 模拟退火算法思想：模仿自然界退火现象而得，利用了物理中固体物质的退火过程与一般优化问题的相似性。
  从某一初始温度开始，伴随温度的不断下降，结合概率突跳特性在解空间中随机寻找全局最优解

6-8 如何确定梯度计算的准确性？调试梯度下降法

# ipynb上的代码，没有print()


import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
X = np.random.random(size = (1000,10))

true_theta = np.arange(1,12,dtype = float)

X_b = np.hstack([np.ones((len(X),1)),X]   )
y = X_b.dot(true_theta) + np.random.normal(size = 1000)

print(X.shape)
print(y.shape)
print(true_theta)

def J(theta,X_b,y):  #定义损失函数
    try:
        return np.sum((y-X_b.dot(theta))**2  ) / len(X_b)  
    except:
        return float("inf")

def dJ_math(theta,X_b,y):  # 定义梯度 数学公式计算
    return X_b.T.dot(X_b.dot(theta) - y)*2. / len(y)

def dJ_debug(theta,X_b,y,epsilon=.01):    # 定义梯度 debug计算 
    res = np.empty(len(theta))
    for i in range(len(theta)):
        theta_1 = theta.copy()
        theta_1[i] += epsilon
        theta_2 = theta.copy()
        theta_2[i] -= epsilon
        res[i] = (J(theta_1,X_b,y) - J(theta_2,X_b,y))/(2*epsilon)
    
    return res

def gradient_descent(dJ,X_b,y,initial_theta,eta=1e-2,epsilon=1e-8,n_iters=1e4):
    theta = initial_theta
    i_iters = 0
    while i_iters < n_iters:
        gradient = dJ(theta,X_b,y)
        last_theta = theta
        theta = theta - eta * gradient
        if (abs(J(theta,X_b,y)-J(last_theta,X_b,y)))< epsilon:
            break
        i_iters += 1 

    return theta

X_b = np.hstack( ( np.ones((len(X),1)),X) )
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01

%time theta = gradient_descent(dJ_debug,X_b,y,initial_theta,eta)
theta

%time theta = gradient_descent(dJ_math,X_b,y,initial_theta,eta)
theta

tip
dJ_debug用于验证调试梯度，速度较慢,可以取少量样本用dJ_debug得到正确的结果，再用公式推出数学解，对比结果。

dJ_debug不受当前损失函数J的影响，求梯度具有普适性。

6-9 有关梯度下降法的更多深入讨论

BGD：每次都需要遍历整个样本，每次向梯度下降最快的方向一定，稳定但是慢。
SGD：每次只看一个样本，梯度下降的方向不确定，甚至可能向反方向移动， 快但是不稳定。

MBGD：两种极端方法折中，每次却k个样本，k也成了一个超参数。

总结：有些相关的代码只能在VSC运行，Jupyter就跑不了，特别是hstack()函数。