当前位置:网站首页>[mathematical logic] predicate logic (judge whether the first-order predicate logic formula is true or false | explain | example | predicate logic formula type | forever true | forever false | satisfi
[mathematical logic] predicate logic (judge whether the first-order predicate logic formula is true or false | explain | example | predicate logic formula type | forever true | forever false | satisfi
2022-07-03 03:53:00 【Programmer community】
List of articles
- One 、 Judge whether the predicate logic formula is true or false ( semantics )
- Two 、 Predicate logic " explain "
- 3、 ... and 、 Predicate logic " explain " Example
- Four 、 Predicate logic formula type
One 、 Judge whether the predicate logic formula is true or false ( semantics )
Predicate logic grammar And semantics :
grammar : The above two sections explain Predicate logic Formula , how Write the formula according to the statement , yes grammar Category ;
semantics : How about the formula written Determine whether it is true or false , Belong to semantics Category ;
Determine whether the formula is true or false :
- Propositional logic : In propositional logic , By assigning values to propositional arguments , And calculate according to the rules of connectives , Finally get the true value , This process is called assignment ;
- First order predicate logic : In first-order predicate logic , Use “ explain ” Method , Determine whether a formula is true or false ;
Two 、 Predicate logic “ explain ”
explain :
Given Predicate logic The formula
A
A
A , The formula
A
A
A from Individual words , The predicate , quantifiers form ;
Individual domain : Appoint The formula
A
A
A Of Individual domain by It is known that Individual domain
D
D
D ;
Individual words : Use specific Individual constant yuan replace
A
A
A Medium Individual words ;
function : Use Specific functions , replace
A
A
A Medium Function arguments ;
The predicate : Use specific The predicate , replace
A
A
A Medium Predicate argument ;
After performing the above operations , You can get
A
A
A One of the formulas “ explain ” ;
assignment And explain :
assignment : assignment yes For propositional logic Propositional argument take
0
,
1
0 , 1
0,1 True or false ;
explain : explain yes to Individual words In the individual domain Specify which individual , to The predicate Specify a specific nature or relationship , to quantifiers Appoint Individual domain Determine its scope , To determine the Individual words , The predicate , quantifiers , You can determine the truth of the formula ;
Given a Predicate logic The formula , Give a explain , Can Determine whether it is true or false ;
The same Predicate logic The formula , There can be Different interpretations ;
- individual Appoint Different individual
- The predicate Appoint Different Nature or relationship
- quantifiers Use different Individual domain Explain ;
3、 ... and 、 Predicate logic “ explain ” Example
Given First order predicate logic The formula
A
A
A by
∀
x
(
F
(
x
)
→
G
(
x
)
)
\forall x ( F(x) \to G(x) )
∀x(F(x)→G(x)) , There are several explanations ;
Explain a :
Individual domain : Set of real numbers ;
F
(
x
)
F(x)
F(x) :
x
x
x It's a reasonable number ;
G
(
x
)
G(x)
G(x) :
x
x
x It's a score ;
At this point, the formula
A
A
A It can be explained as : Rational numbers can be expressed as fractions ;
At this time, the corresponding proposition of this explanation is True proposition ;
Explain two :
Individual domain : Total individual domain ;
F
(
x
)
F(x)
F(x) :
x
x
x Is the person ;
G
(
x
)
G(x)
G(x) :
x
x
x Hair is black ;
At this point, the formula
A
A
A It can be explained as : Everyone has black hair ;
At this time, the corresponding proposition of this explanation is False proposition ;
Four 、 Predicate logic formula type
Predicate logic The formula , With the explanation , You can judge the type of formula ;
Predicate logic Formula types are divided into Yongzhen style , Permanent falsehood , Satisfiability , Equivalent formula etc. ;
- Yongzhen style : The formula
A
A
A stay Any explanation is true ;
- Permanent falsehood : The formula
A
A
A stay Any explanation is false ;
- Satisfiability : The formula
A
A
A There is at least one true explanation ;
- Equivalency : If
A
B
A \leftrightarrow B
A
A
A and
B
B
B Is equivalent , Write it down as
A
⇔
B
A \Leftrightarrow B
A⇔B , call
A
⇔
B
A \Leftrightarrow B
A⇔B Is equivalent ;
AB It's Yongzhen style , The formula
边栏推荐
- 2022 mobile crane driver examination registration and mobile crane driver operation examination question bank
- 【刷题篇】多数元素(超级水王问题)
- Nodejs Foundation: shallow chat URL and querystring module
- sigaction的使用
- C language hashtable/hashset library summary
- Reflection and planning of a sophomore majoring in electronic information engineering
- Mongodb master profile
- TCP, the heavyweight guest in tcp/ip model -- Kuige of Shangwen network
- [combinatorics] basic counting principle (addition principle | multiplication principle)
- 没有sXid,suid&sgid将进入险境!-尚文网络xUP楠哥
猜你喜欢

Introduction to mongodb
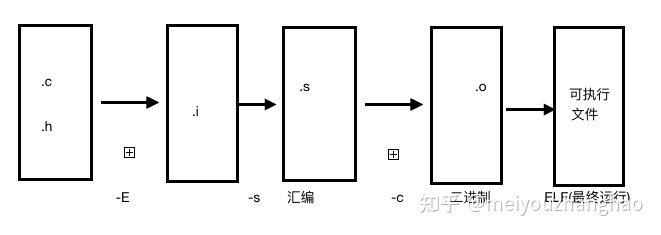
Makefile demo

NPM: the 'NPM' item cannot be recognized as the name of a cmdlet, function, script file, or runnable program. Please check the spelling of the name. If the path is included, make sure the path is corr

2022 tea master (intermediate) examination questions and analysis and tea master (intermediate) practical examination video
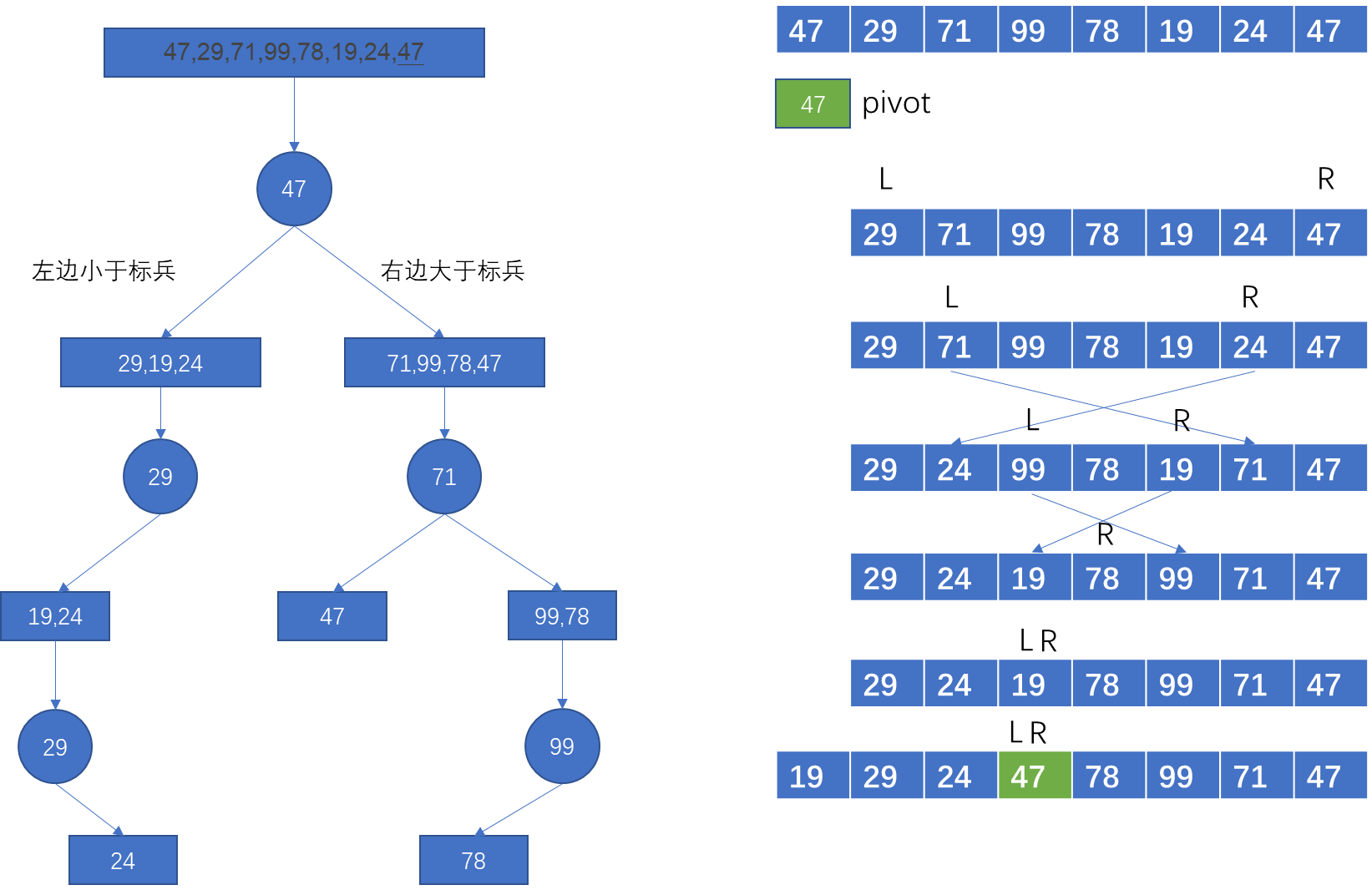
递归:快速排序,归并排序和堆排序
![[home push IMessage] software installation virtual host rental tothebuddy delay](/img/e7/eb20a773e4b674962f856d179a3769.jpg)
[home push IMessage] software installation virtual host rental tothebuddy delay

学会pytorch能干什么?

docker安装及启动mysql服务

What is pytorch? Is pytorch a software?

小程序获取用户头像和昵称
随机推荐
Recursive use and multi-dimensional array object to one-dimensional array object
2022 Shandong Province safety officer C certificate examination questions and Shandong Province safety officer C certificate simulation examination question bank
2022 tea master (primary) examination questions and tea master (primary) examination question bank
Bisher - based on SSM pet adoption center
Mongodb installation & Deployment
毕设-基于SSM宠物领养中心
Summary of electromagnetic spectrum
pytorch是什么?pytorch是一个软件吗?
Error c2694 "void logger:: log (nvinfer1:: ilogger:: severity, const char *)": rewrite the restrictive exception specification of virtual functions than base class virtual member functions
[daily question] dichotomy - find a single dog (Bushi)
Shardingsphere dynamic data source
Docker install and start MySQL service
What is pytorch? Is pytorch a software?
[Blue Bridge Road - bug free code] pcf8591 - code analysis of AD conversion
pytorch项目怎么跑?
Use of sigaction
navicat 导出数据库的表结构
[mathematical logic] propositional logic (judgment of the correctness of propositional logic reasoning | formal structure is eternal truth - equivalent calculus | deduction from premise - logical reas
阿洛对自己的思考
2020-01-01t00:00:00.000000z date format conversion