当前位置:网站首页>[mathematical logic] propositional logic (judgment of the correctness of propositional logic reasoning | formal structure is eternal truth - equivalent calculus | deduction from premise - logical reas
[mathematical logic] propositional logic (judgment of the correctness of propositional logic reasoning | formal structure is eternal truth - equivalent calculus | deduction from premise - logical reas
2022-07-03 03:40:00 【Programmer community】
List of articles
- One 、 Judgment of the correctness of propositional logic reasoning
- Two 、 The formal structure is forever true ( Equivalent calculus )
- 3、 ... and 、 Deduce the conclusion from the premise ( logical reasoning )
One 、 Judgment of the correctness of propositional logic reasoning
Propositional reasoning , according to Premise , Reasoning out Conclusion ;
Such as :
Premise : yes
p
→
(
q
→
r
)
p \to (q \to r)
p→(q→r) ,
p
p
p ,
q
q
q ;
Conclusion : yes
r
r
r
How to judge according to the above premise , The reasoning conclusion is correct ?
The law of reasoning :
A
,
B
A,B
A,B There are two propositions , If
A
→
B
A \to B
A→B It's Yongzhen style , that
A
⇒
B
A \Rightarrow B
A⇒B ;
The formal structure of reasoning
Premise :
A
1
,
A
2
,
⋯
,
A
k
A_1 , A_2 , \cdots , A_k
A1,A2,⋯,Ak
Conclusion :
B
B
B
The formal structure of reasoning is :
(
A
1
∧
A
2
∧
⋯
∧
A
k
)
→
B
(A_1 \land A_2 \land \cdots \land A_k) \to B
(A1∧A2∧⋯∧Ak)→B
Propositional logic The correctness of reasoning determine , There are two ways ;
Method 1 : Write inferential Formal structure , Check whether the formal structure of the reasoning is Yongzhen style ; If it is Yongzhen , Then the reasoning is correct ;
Method 2 : from Premise Deduce Conclusion , according to Equivalence calculus rules , Rules of reasoning , Make a deduction ;
Two 、 The formal structure is forever true ( Equivalent calculus )
Equivalent calculus reference blog : 【 Mathematical logic 】 Propositional logic ( Equivalent calculus | Idempotent law | Commutative law | Associative law | Distributive law | De Morgan law | absorptivity | Law of zero | The same thing | The law of excluded middle | Law of contradiction | Double negative rate | Implication equivalence … )
Premise :
p
→
(
q
→
r
)
p \to (q \to r)
p→(q→r) ,
p
p
p ,
q
q
q ;
Conclusion :
r
r
r
The formal structure of reasoning is :
(
p
→
(
q
→
r
)
)
∧
p
∧
q
→
r
(p \to (q \to r)) \land p \land q \to r
(p→(q→r))∧p∧q→r
Use Equivalent calculus Methods , Verify whether the above formal structure is Yongzhen style ;
Connective The priority for :“
¬
\lnot
¬” Greater than “
∧
,
∨
\land , \lor
∧,∨” Greater than “
→
,
\to, \leftrightarrow
→,” ; Start with the higher priority ;
(
p
→
(
q
→
r
)
)
∧
p
∧
q
→
r
(p \to (q \to r)) \land p \land q \to r
(p→(q→r))∧p∧q→r
Implication equivalence : Use Implication equivalence The rules , Put the above
(
p
→
(
q
→
r
)
)
(p \to (q \to r))
(p→(q→r)) Perform equivalent calculus :
⇔
(
¬
p
∨
(
¬
q
∨
r
)
)
∧
p
∧
q
→
r
\Leftrightarrow (\lnot p \lor (\lnot q \lor r)) \land p \land q \to r
⇔(¬p∨(¬q∨r))∧p∧q→r
Distribution rate : according to Distribution rate , Calculation
(
¬
p
∨
(
¬
q
∨
r
)
)
∧
p
(\lnot p \lor (\lnot q \lor r)) \land p
(¬p∨(¬q∨r))∧p part :
⇔
(
(
¬
p
∧
p
)
∨
(
(
¬
q
∨
r
)
∧
p
)
)
∧
q
→
r
\Leftrightarrow (( \lnot p \land p ) \lor ( (\lnot q \lor r) \land p ) ) \land q \to r
⇔((¬p∧p)∨((¬q∨r)∧p))∧q→r
Law of contradiction : among according to Law of contradiction You know ,
¬
p
∧
p
⇔
0
\lnot p \land p \Leftrightarrow 0
¬p∧p⇔0 :
⇔
(
0
∨
(
(
¬
q
∨
r
)
∧
p
)
)
∧
q
→
r
\Leftrightarrow ( 0 \lor ( (\lnot q \lor r) \land p ) ) \land q \to r
⇔(0∨((¬q∨r)∧p))∧q→r
The same thing : according to The same thing ,
0
∨
(
(
¬
q
∨
r
)
∧
p
)
0 \lor ( (\lnot q \lor r) \land p )
0∨((¬q∨r)∧p) And
(
¬
q
∨
r
)
∧
p
(\lnot q \lor r) \land p
(¬q∨r)∧p It is equivalent. :
⇔
(
(
¬
q
∨
r
)
∧
p
)
∧
q
→
r
\Leftrightarrow ( (\lnot q \lor r) \land p ) \land q \to r
⇔((¬q∨r)∧p)∧q→r
Associative law : according to Associative law , To recombine
(
(
¬
q
∨
r
)
∧
p
)
∧
q
( (\lnot q \lor r) \land p ) \land q
((¬q∨r)∧p)∧q by
(
(
¬
q
∨
r
)
∧
q
)
∧
p
( (\lnot q \lor r) \land q ) \land p
((¬q∨r)∧q)∧p :
⇔
(
(
¬
q
∨
r
)
∧
q
)
∧
p
→
r
\Leftrightarrow ( (\lnot q \lor r) \land q ) \land p \to r
⇔((¬q∨r)∧q)∧p→r
Distribution rate : according to Distribution rate , Calculation
(
¬
q
∨
r
)
∧
q
(\lnot q \lor r) \land q
(¬q∨r)∧q , The result is
(
¬
q
∧
q
)
∨
(
r
∧
q
)
(\lnot q \land q) \lor (r \land q)
(¬q∧q)∨(r∧q)
⇔
(
(
¬
q
∧
q
)
∨
(
r
∧
q
)
)
∧
p
→
r
\Leftrightarrow ( (\lnot q \land q) \lor (r \land q) ) \land p \to r
⇔((¬q∧q)∨(r∧q))∧p→r
Law of contradiction : according to Law of contradiction Calculation
¬
q
∧
q
\lnot q \land q
¬q∧q , As a result,
0
0
0 :
⇔
(
0
∨
(
r
∧
q
)
)
∧
p
→
r
\Leftrightarrow ( 0 \lor (r \land q) ) \land p \to r
⇔(0∨(r∧q))∧p→r
The same thing : According to the same ,
0
∨
(
r
∧
q
)
0 \lor (r \land q)
0∨(r∧q) Equivalent to
(
r
∧
q
)
(r \land q)
(r∧q) :
⇔
(
r
∧
q
)
∧
p
→
r
\Leftrightarrow (r \land q) \land p \to r
⇔(r∧q)∧p→r
Connective priority :
(
r
∧
q
)
∧
p
(r \land q) \land p
(r∧q)∧p in , The conjunctions have the same priority , Brackets can be deleted , Put three propositions in a bracket ;
⇔
(
r
∧
q
∧
p
)
→
r
\Leftrightarrow (r \land q \land p ) \to r
⇔(r∧q∧p)→r
Implication equivalence : according to Implication equivalence , elimination Implicative connectives
→
\to
→ :
⇔
¬
(
r
∧
q
∧
p
)
∨
r
\Leftrightarrow \lnot (r \land q \land p) \lor r
⇔¬(r∧q∧p)∨r
De Morgan law : according to De Morgan law , Assign a negative sign in parentheses ;
⇔
(
¬
r
∨
¬
q
∨
¬
p
)
∨
r
\Leftrightarrow (\lnot r \lor \lnot q \lor \lnot p ) \lor r
⇔(¬r∨¬q∨¬p)∨r
Connective priority :
(
¬
r
∨
¬
q
∨
¬
p
)
∨
r
(\lnot r \lor \lnot q \lor \lnot p ) \lor r
(¬r∨¬q∨¬p)∨r in , The conjunctions have the same priority , Brackets can be deleted , Put three propositions in a bracket ;
⇔
¬
r
∨
¬
q
∨
¬
p
∨
r
\Leftrightarrow \lnot r \lor \lnot q \lor \lnot p \lor r
⇔¬r∨¬q∨¬p∨r
The law of excluded middle : According to the law of exclusion ,
¬
r
∨
r
\lnot r \lor r
¬r∨r And
1
1
1 Equivalent ;
⇔
1
∨
¬
q
∨
¬
p
\Leftrightarrow 1 \lor \lnot q \lor \lnot p
⇔1∨¬q∨¬p
Law of zero : According to the zero law ,
1
1
1 Extract any value , Are equivalent to
1
1
1 :
⇔
1
\Leftrightarrow 1
⇔1
3、 ... and 、 Deduce the conclusion from the premise ( logical reasoning )
Logical reasoning reference blog : 【 Mathematical logic 】 Propositional logic ( Propositional logic inference | The formal structure of reasoning | The law of reasoning | Additional law | The law of simplification | Hypothetical reasoning | Reject | Disjunctive syllogism | Hypothetical syllogism | Equivalent syllogism | constructive dilemma )
Premise :
p
→
(
q
→
r
)
p \to (q \to r)
p→(q→r) ,
p
p
p ,
q
q
q ;
Conclusion :
r
r
r
Connect the prerequisites with conjunctive connectives ,
(
p
→
(
q
→
r
)
)
∧
p
∧
q
(p \to (q \to r)) \land p \land q
(p→(q→r))∧p∧q , Perform equivalent calculus , To calculate the
r
r
r ;
(
p
→
(
q
→
r
)
)
∧
p
∧
q
(p \to (q \to r)) \land p \land q
(p→(q→r))∧p∧q
Equivalent calculus Associative law :
⇔
(
(
p
→
(
q
→
r
)
)
∧
p
)
∧
q
\Leftrightarrow ((p \to (q \to r)) \land p) \land q
⇔((p→(q→r))∧p)∧q
logical reasoning Hypothetical reasoning :
(
A
→
B
)
∧
A
⇒
B
( A \to B ) \land A \Rightarrow B
(A→B)∧A⇒B , So from
(
p
→
(
q
→
r
)
)
∧
p
(p \to (q \to r)) \land p
(p→(q→r))∧p It can be inferred that
q
→
r
q \to r
q→r ;
⇒
(
q
→
r
)
∨
q
\Rightarrow (q \to r) \lor q
⇒(q→r)∨q
logical reasoning Hypothetical reasoning :
(
A
→
B
)
∧
A
⇒
B
( A \to B ) \land A \Rightarrow B
(A→B)∧A⇒B , So from
(
q
→
r
)
∨
q
(q \to r) \lor q
(q→r)∨q It can be inferred that
r
r
r ;
⇒
r
\Rightarrow r
⇒r
logical reasoning Than Equivalent calculus fast , Equivalent calculus is more intuitive , Logical reasoning needs to choose the appropriate reasoning law ;
边栏推荐
- redis在服务器linux下的启动的相关命令(安装和配置)
- Pat class B common function Usage Summary
- 简易版 微信小程序开发之for指令、上传图片及展示效果优化
- Pytoch lightweight visualization tool wandb (local)
- C # webrequest post mode, based on "basic auth" password authentication mode, uploads files and submits other data using multipart / form data mode
- Ffmpeg recording screen and screenshot
- Web session management security issues
- Vs 2019 configuration tensorrt
- Tidal characteristics of the Bohai Sea and the Yellow Sea
- com. fasterxml. jackson. databind. Exc.invalidformatexception problem
猜你喜欢

Captura下载安装及在Captura配置FFmpeg

Limit of one question per day

Vs 2019 configuration tensorrt
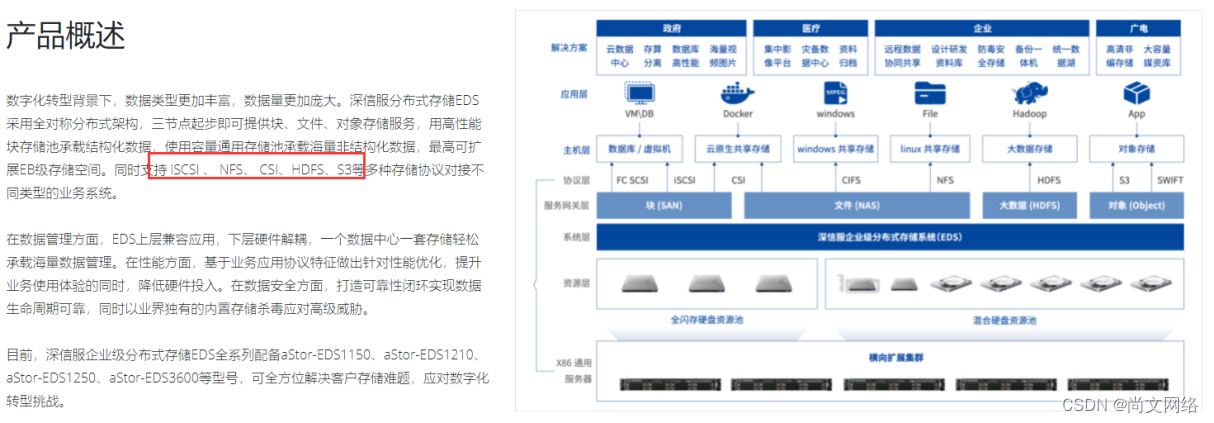
释放数据力量的Ceph-尚文网络xUP楠哥
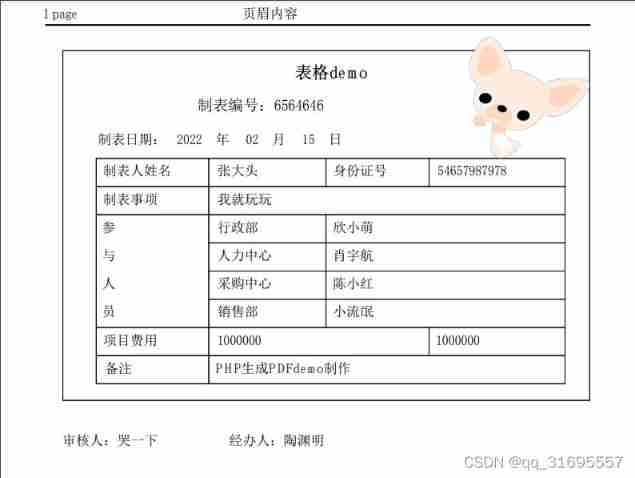
PHP generates PDF tcpdf

Don't use the new Dede collection without the updated Dede plug-in

没有sXid,suid&sgid将进入险境!-尚文网络xUP楠哥

Web会话管理安全问题
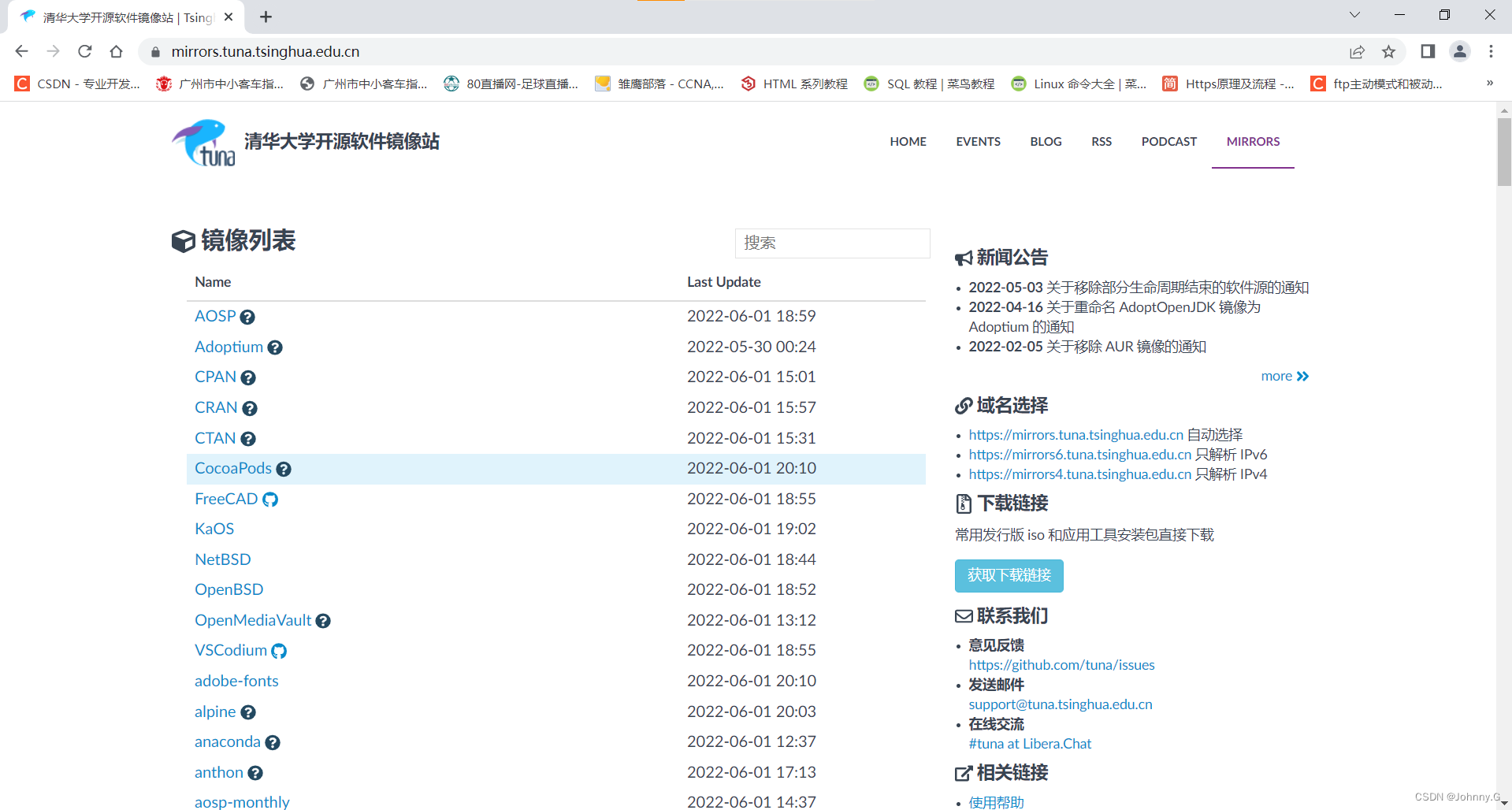
Mongodb installation & Deployment
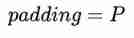
The calculation of stripe, kernel and padding in CNN
随机推荐
Tidal characteristics of the Bohai Sea and the Yellow Sea
[embedded module] OLED display module
[mathematical logic] propositional logic (propositional logic reasoning | formal structure of reasoning | inference law | additional law | simplification law | hypothetical reasoning | refusal | disju
Hi3536C V100R001C02SPC040 交叉编译器安装
简易版 微信小程序开发之for指令、上传图片及展示效果优化
node 开启服务器
Web会话管理安全问题
Recursion: depth first search
Réglez la hauteur et lancez le système. Currenttimemillis catton
MongoDB主配置文件
ffmpeg之 一张/多张图片合成视频
8.8.2-PointersOnC-20220214
The series of hyperbolic function in daily problem
Docker install and start MySQL service
Error in compiled file: error: unmapped character encoding GBK
ffmpeg下载安装教程及介绍
FileZilla client download and installation
[AI practice] Application xgboost Xgbregressor builds air quality prediction model (I)
Elsevier latex 提交文章 pdftex.def Error: File `thumbnails/cas-email.jpeg‘ not found: using draf
Don't use the new Dede collection without the updated Dede plug-in