当前位置:网站首页>动态规划:最长公共子串和最长公共子序列
动态规划:最长公共子串和最长公共子序列
2022-07-03 03:28:00 【我家大宝最可爱】
最长公共子串
给定两个字符串,求出最长的相同的子串,例如给定子串asdfas和werasdfaswer,其中两个子串串中共有的最长子串就是asdfas这个字符串。
同样,这道题一看就是动态规划,我们首先列出状态转移方程,假设两个字符串分别以i,j为结尾的最长公共子串长度为dp[i][j],当A[i]==B[j]时,dp[i][j]=dp[i-1][j-1]+1,如果这两个字符不相等,也就是说以A[i],B[j]为结尾的这两个字符串就不是公共子串,此时dp[i][j]=0
| a | s | d | f | a | s | ||||
| w | e | r | a | s | d | f | a | s | w |
s1 = input()
s2 = input()
n1 = len(s1)
n2 = len(s2)
dp = [[0 for _ in range(n2)] for _ in range(n1)]
max_len = 0
for i,x in enumerate(s1):
for j,y in enumerate(s2):
if x == y:
if i == 0 or j == 0:
dp[i][j] = 1
else:
dp[i][j] = dp[i-1][j-1] + 1
if dp[i][j] > max_len:
max_len = dp[i][j]
print(max_len)
最长公共子序列
公共子序列不需要连续,因此,即使两个字符串不相等,dp[i][j]也不会为0。当前两个字符不等,t1[i]!=t2[j]的话,那么长度最少也是dp[i-1][j-1],但这还不够,因为我们希望拿到之前的比较中尽可能大的长度。那么当前字符已经不相等的情况下,就应该把当前的字符也放入到之前的比较中,那么一定有dp[i][j-1]和dp[i-1][j]>=dp[i][j]。简单来说,dp[i][j]的值应该从dp[i-1][j-1],dp[i][j-1],dp[i-1][j]三者中取,但dp[i][j]≤另外两个,故比较另外两个,取较大的。
我们定义的状态表示f数组和text数组下标均是从1开始的,而题目给出的text数组下标是从0开始的,为了一 一对应,在判断text1和text2数组的最后一位是否相等时,往前错一位,即使用text1[i - 1]和text2[j - 1]来判断。
这里解释一下为什么f数组和text数组均定义成下标从1开始。原因是因为状态转移方程 f[i][j] = max(f[i - 1][j],f[i][j - 1]), 当我们的f数组定义成下标从1开始以后,我们就可以在代码中不用对下标越界问题做出额外判断。其实我们也可以发现一个问题,就是题目给定的原数组,比如text数组,如果下标从1开始的话,状态表示会更加的清晰,推导状态转移方程的过程也会更加好理解。
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
m, n = len(text1), len(text2)
dp = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if text1[i - 1] == text2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
return dp[m][n]
边栏推荐
- Nce detail of softmax approximation
- float与0比较
- Mongodb master profile
- Bid farewell to artificial mental retardation: Mengzi open source project team received RMB 100 million financing to help NLP develop
- PAT乙级常用函数用法总结
- Use of El tree search method
- MongoDB基本操作【增、删、改、查】
- leetcode:动态规划模板
- 小程序获取用户头像和昵称
- 为什么线程崩溃不会导致 JVM 崩溃
猜你喜欢

Vs 2019 configuration du moteur de génération de tensorrt

Bid farewell to artificial mental retardation: Mengzi open source project team received RMB 100 million financing to help NLP develop
PHP generates PDF tcpdf

softmax的近似之NCE详解

为什么线程崩溃不会导致 JVM 崩溃

Pytorch轻量级可视化工具wandb(local)

Nanning water leakage detection: warmly congratulate Guangxi Zhongshui on winning the first famous brand in Guangxi
Unity3d RPG implementation (medium)
Pytorch multi card distributed training distributeddataparallel usage
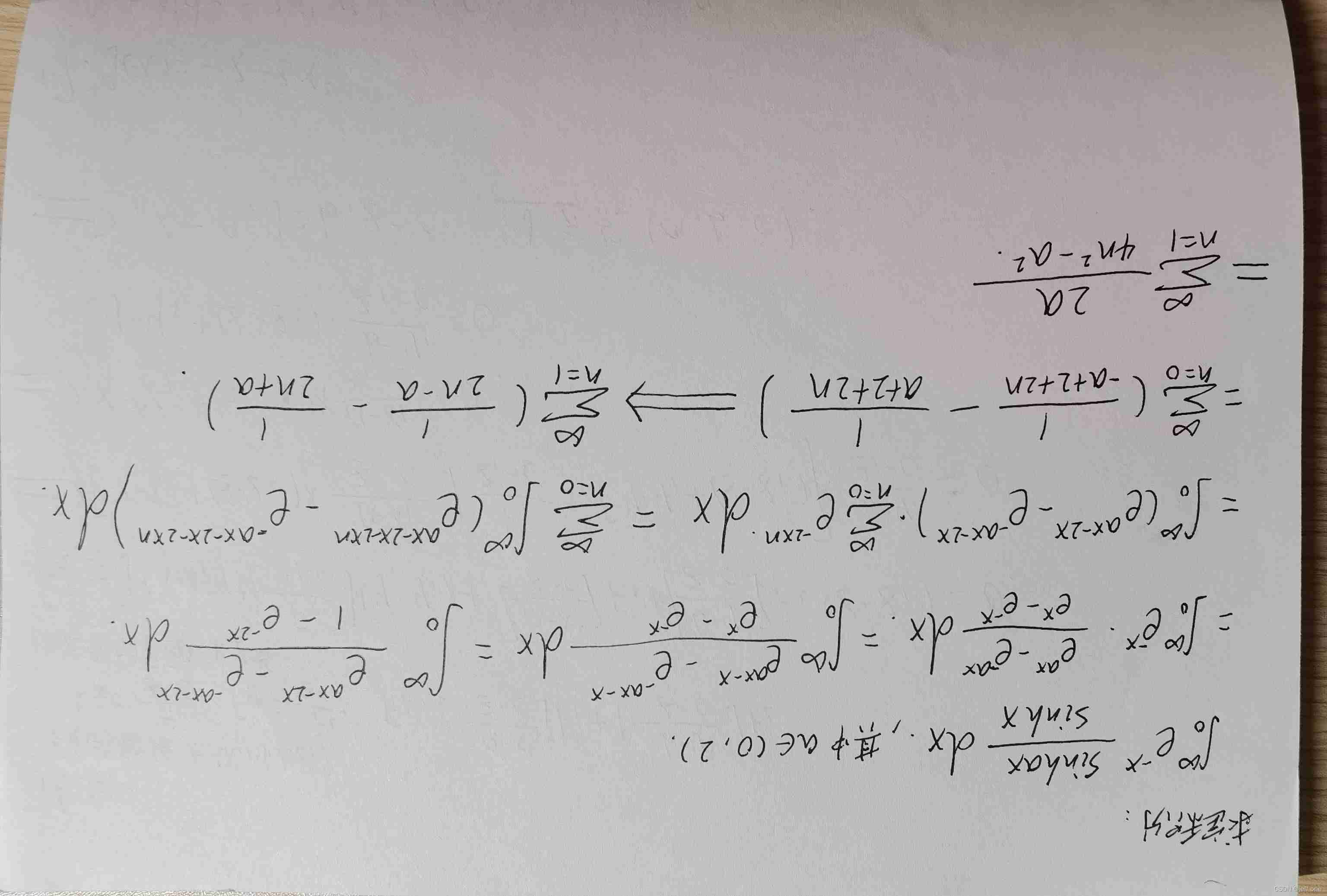
The series of hyperbolic function in daily problem
随机推荐
Convert binary stream to byte array
VS code配置虚拟环境
Agile certification (professional scrum Master) simulation exercises
Nanning water leakage detection: warmly congratulate Guangxi Zhongshui on winning the first famous brand in Guangxi
递归使用和多维数组对象变一维数组对象
[combinatorics] Application of exponential generating function (multiple set arrangement problem | different balls in different boxes | derivation of exponential generating function of odd / even sequ
C programming learning notes [edited by Mr. Tan Haoqiang] (Chapter III sequence programming) 05 data input and output
900w+ data, from 17s to 300ms, how to operate
shardingsphere动态数据源
Ansible简介【暂未完成(半成品)】
MongoDB简介
[leetcode question brushing day 34] 540 Unique element in array, 384 Disrupt array, 202 Happy number, 149 Maximum number of points on a line
UMI route interception (simple and rough)
VS 2019 配置tensorRT生成engine
Idea format code idea set shortcut key format code
为什么线程崩溃不会导致 JVM 崩溃
Use of El tree search method
[set theory] partial order relation (partial order relation definition | partial order set definition | greater than or equal to relation | less than or equal to relation | integer division relation |
Mongodb replication set [master-slave replication]
docker安装及启动mysql服务