当前位置:网站首页>概率与期望部分题解
概率与期望部分题解
2022-08-05 05:40:00 【litian355】
找BUG
dp[i][j]表示已经找到i种bug,j个系统的bug,达到目标状态的天数的期望
dp[n][s]=0;要求的答案是dp[0][0];
dp[i][j]可以转化成以下四种状态:
dp[i][j],发现一个bug属于已经有的i个分类和j个系统。概率为(i/n)*(j/s);
dp[i][j+1],发现一个bug属于已有的分类,不属于已有的系统.概率为 (i/n)*(1-j/s);
dp[i+1][j],发现一个bug属于已有的系统,不属于已有的分类,概率为 (1-i/n)*(j/s);
dp[i+1][j+1],发现一个bug不属于已有的系统,不属于已有的分类,概率为 (1-i/n)*(1-j/s);整理便得到转移方程
code:
#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;
const int MAXN=1010;
double dp[MAXN][MAXN];
int main()
{
int n,s;
while(scanf("%d%d",&n,&s)!=EOF)
{
dp[n][s]=0;
for(int i=n;i>=0;i--)
for(int j=s;j>=0;j--)
{
if(i==n&&j==s)continue;
dp[i][j]=(i*(s-j)*dp[i][j+1]+(n-i)*j*dp[i+1][j]+(n-i)*(s-j)*dp[i+1][j+1]+n*s)/(n*s-i*j);
}
printf("%.4lf\n",dp[0][0]);//POJ上G++要改成%.4f
}
return 0;
}扑克牌
事件发生的期望的线性性E(aX+bY)=aE(X)+bE(Y)=p(X)×E(X)+p(Y)×E(Y)
将问题转为图
起点->终点的路径的期望长度
点(状态) 边(状态转移)
f[a][b][c][d][x][y]:从当前状态跳到终点的期望长度f[a][b][c][d][x][y]:从当前状态跳到终点的期望长度
a张黑桃,b张红桃,c张梅花,d张方块a张黑桃,b张红桃,c张梅花,d张方块
大王状态x,小王状态y:0∼3表示放到abcd4堆中,4表示没有被翻出来大王状态x,小王状态y:0∼3表示放到abcd4堆中,4表示没有被翻出来
则我们只需分析f[a][b][c][d][x][y]能够转移成哪些状态,期望就能用线性公式转移得到
![min3i=01sumf[a][b][c][d][i][y]+min3j=01sumf[a][b][c][d][x][j]](http://img.inotgo.com/imagesLocal/202208/05/202208050540062695_2.gif)
#include<bits/stdc++.h>
using namespace std;
#define db double
typedef long long LL;
const LL N=14;
const db INF=1e20;
db f[N][N][N][N][5][5];
int A,B,C,D;
db dp(int a,int b,int c,int d,int x,int y){
auto &v=f[a][b][c][d][x][y];
if(v>=0) return v;
if((a+(x==0)+(y==0)>=A)&&(b+(x==1)+(y==1)>=B)&&(c+(x==2)+(y==2)>=C)&&(d+(x==3)+(y==3)>=D))
return v=0;
int sum=a+b+c+d+(x!=4)+(y!=4);
sum=54-sum;
if(sum<=0) return INF;
v=1;
if(a<13) v+=(13.0-a)/sum*dp(a+1,b,c,d,x,y);
if(b<13) v+=(13.0-b)/sum*dp(a,b+1,c,d,x,y);
if(c<13) v+=(13.0-c)/sum*dp(a,b,c+1,d,x,y);
if(d<13) v+=(13.0-d)/sum*dp(a,b,c,d+1,x,y);
if(x==4)
{
double t=INF;
for(int i=0;i<4;i++){
t=min(t,dp(a,b,c,d,i,y)/sum);
}
v+=t;
}
if(y==4){
db t=INF;
for(int i=0;i<4;i++){
t=min(t,dp(a,b,c,d,x,i)/sum);
}
v+=t;
}
return v;
}
signed main(){
cin>>A>>B>>C>>D;
memset(f,-1,sizeof f);
auto v=dp(0,0,0,0,4,4);
if(v>=INF/2) v=-1;
printf("%.3lf",v);
return 0;
}Alice和Bob赌糖果
赌徒模型:
建立一个通用模型,两个赌徒甲,乙进行赌博,,每一局输者要付给胜者1元,开始时,甲的资本n,乙的资本是m,直到甲或乙输光,赌博结束,求甲获得所有资本的概率?
假设 A获胜概率是p,失败概率是q,平局概率是1-p-q;
显然游戏最多进行m+n-1局
设为资金在i情况下,资金变为n+m的概率,后面简写为,易知,,根据之前的结论可以分析出:
所以,当甲、乙双方获胜概率相等时,甲获得所有资本的概率为,乙获得所有资本的概率为
。
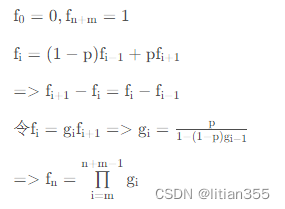
code
#include <bits/stdc++.h>
using namespace std;
#define double long double
int main() {
int n, l, r; cin >> n >> l >> r;
int m, L, R; cin >> m >> L >> R;
if(m == 0) cout << "1.00000" << '\n';
else if(n == 0) cout << "0.00000" << '\n';
else {
double ali = 0, bob = 0;
for(int i = l; i <= r; ++ i) {
for(int j = L; j <= R; ++ j) {
if(i > j) ali ++;
if(i < j) bob ++;
}
}
if(ali == 0) cout << "0.00000" << '\n';
else {
double p = ali / (ali + bob);
double q = 1.0 - p;
vector<double> g(n + m + 1);
for(int i = 1; i < n + m; ++ i) {
g[i] = p / (1.0 - q * g[i - 1]);
}
double res = 1.0;
for(int i = n; i < n + m; ++ i) res *= g[i];
cout << fixed << setprecision(5) << res << '\n';
}
}
return 0;
}概率充电器 NC20589
考虑算出每个点的概率 、Pi,利用期望的线性性, 就是答案。
就是答案。
考虑先求出每个点通过自己或是子树的点通电的概率,设为 fi。
考虑加上一个子树时,概率怎么转移,设 w 为根 u 从子节点 v 及其子树通电的概率,即  ,这里 pu,v 表示连接 u,v 的导线的通电概率。 那么
,这里 pu,v 表示连接 u,v 的导线的通电概率。 那么  。
。
这里利用了一个小的容斥,即 P(A∪B)=P(A)+P(B)−P(A∩B)=P(A)+P(B)−P(A)×P(B)。
然后考虑点 u 如何从父亲 fa 处转移,此时要算出 fa 不从 u 走时通电的概率,设为Pa。
仿照开始求 f 的过程,令 w=fu×pu,fa,则有 fa=Pa+w−Pa×w。
所以 Pa=1−wffa−w。(当w=1 时该式无意义,强行计算会导致 RE)。
所以 fafa 的子节点 uu 真正通电的概率P(u)=fu+(Pa×pu,fa)−fu×(Pa×pu,fa)。
复杂度 O(n)。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
inline void read(int &x)
{
x = 0;
int f = 0;
char ch = getchar();
while(ch < '0' || ch > '9')
{
f |= ch == '-';
ch = getchar();
}
while(ch >= '0' && ch <= '9')
{
x = x * 10 + ch - 48;
ch = getchar();
}
x = f ? -x : x;
return;
}
#define N 500005
int first[N], Next[N << 1], to[N << 1], tot;
double w[N << 1];
inline void add(int &x, int &y, double &z)
{
Next[++tot] = first[x];
first[x] = tot;
to[tot] = y;
w[tot] = z;
return;
}
double f[N];
void dfs1(int u, int pre)
{
for(int i = first[u]; i; i = Next[i])
{
int v = to[i];
if(v == pre)
{
continue;
}
dfs1(v, u);
f[u] = f[u] + w[i] * f[v] - f[u] * w[i] * f[v];
}
return;
}
void dfs2(int u, int pre)
{
for(int i = first[u]; i; i = Next[i])
{
int v = to[i];
if(v == pre)
{
continue;
}
if(f[v] * w[i] != 1)
{
double Pa = w[i] * (f[u] - f[v] * w[i]) / (1 - f[v] * w[i]);
f[v] = f[v] + Pa - f[v] * Pa;
}
dfs2(v, u);
}
return;
}
int n;
signed main()
{
int x, y;
double z;
read(n);
for(int i = 1; i < n; i++)
{
read(x), read(y);
scanf("%lf", &z);
z /= 100.0;
add(x, y, z);
add(y, x, z);
}
for(int i = 1; i <= n; i++)
{
scanf("%lf", &f[i]);
f[i] /= 100.0;
}
dfs1(1, 0);
dfs2(1, 0);
double ans = 0.0;
for(int i = 1; i <= n; i++)
{
ans += f[i];
}
printf("%0.6lf", ans);
return 0;
}Acwing 216. Rainbow的信号
题目描述
Freda发明了传呼机之后,rainbow进一步改进了传呼机发送信息所使用的信号。
由于现在是数字、信息时代,rainbow发明的信号用N个自然数表示。
为了避免两个人的对话被大坏蛋VariantF偷听,rainbow把对话分成A、B、C三部分,分别用a、b、c三个密码加密。
现在Freda接到了rainbow的信息,她的首要工作就是解密。
Freda了解到,这三部分的密码计算方式如下:
在1~N这N个数中,等概率地选取两个数l、r,如果l>r,则交换l、r。把信号中的第l个数到第r个数取出来,构成一个数列P。
A部分对话的密码是数列P的xor和的数学期望值,xor和就是数列P中各个数异或之后得到的数; xor和的期望就是对于所有可能选取的l、r,所得到的数列的xor和的平均数。
B部分对话的密码是数列P的and和的期望,定义类似于xor和。
C部分对话的密码是数列P的or和的期望,定义类似于xor和。
请你帮忙计算这三个密码。
思路
蒟蒻的思路当然是来自《算法竞赛进阶指南》,只是加入一些自己的理解。
按位计算答案。枚举二进制下的每个数位,数的大小不超过10^9^,所以最多枚举到30位。
对每一位,枚举1到n每个数,把当前枚举的第k个数当做选取范围的右端点r,利用先前维护的值来更新答案。
设当前的枚举的数位为k,当前枚举的是第r个数,当前第r个数的数位的值为v(0或1)。
首先知道:l = r 的情况概率为 1 / n^2,其他情况均为 2 / n^2(因为有( l , r ) , ( r , l )两种选法,当r>l时二者交换),在加入答案时注意乘以2。
当前数位的值v为1时
因为有l = r 的情况,所以xor,and,or的答案都要加上该数位的值(若是第3数位则值为100即十进制下的4)除以n^2^的概率(设为pos)。
对于 or 和,l 取 r 前面的任意值,[ l, r ]的或(or)值都为1,共有(r-1)种情况,对答案 ansor 贡献(r-1)* pos。
对于 and 和,我们用 last[v]表示上个v出现的位置,只有当前数位的值为1时才能加入答案,因为如果 [ l, r ] 区间有一个值为0则and值立刻变成0了。而 l 的取值范围的数位 k 的值必须为1,这时候就需要用到 last 数组,l 可以选择的区间即为 [ last[0]+1,r ] 。
当前数位的值v为0时
对于 or 和,l 可以取的区间中的数位值必须有一个 1 ,这样异或后的值才会为一,因为last[1] 到 r 之间的数位值都是0,所以该区间不能取,可取的区间为 [1,last[1] ]。
xor 和的讨论有点麻烦,单独列出来。
对于某个数位上,1到n各个数在该数位的数位值,当前为第 r 个数:
以1为边界将区间分段,为方便理解我将它们编个号:
当l取1、3、5区间时,[ l , r ] 数位值的xor和为0;l取2、4、6区间时,[ l , r ] 数位值的xor和为1。
发现了吗,每个区间都只有一个1。异或0对xor和的值无影响;而每异或一次1,xor和的值就会由1变0或由0变1,所以我们用c1表示奇数区间包含的值的个数,c2表示偶数区间包含的值的个数。
当前数位值为0,l 有c2个可能取值使 [ l , r ] 的xor和为1;当前数位值为1,l 有c1个可能取值使 [ l , r ] 的xor和为1。
c1,c2的维护可通过看下面的代码理解代码:
代码:
#include<bits/stdc++.h>
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=-1; ch=getchar();}
while(ch>='0'&&ch<='9') {x=x*10+ch-'0'; ch=getchar();}
return x*f;
}
const int maxn=1e5+5;
int n,c1,c2;
int w[maxn],p[maxn],last[2];
double ansxor,ansand,ansor;
void solve(int k)
{
c1=c2=0;
last[0]=last[1]=0;
double pos=(double)(1<<k)/n/n;//当前数位的实际值/n方的概率
for(int r=1;r<=n;r++)
{
int v=((w[r]>>k)&1);
if(v)
{
ansxor+=pos;
ansand+=pos;
ansor+=pos;
}
if(v)
{
ansor+=pos*(r-1)*2;
ansand+=pos*(r-1-last[0])*2;
ansxor+=pos*c1*2;
}
else
{
ansor+=pos*last[1]*2;
ansxor+=pos*c2*2;
}
++c1;
if(v) swap(c1,c2);
last[v]=r;
}
}
int main()
{
//freopen("input.txt","r",stdin);
n=read();
for(int i=1;i<=n;i++) w[i]=read();
for(int i=0;i<=30;i++) solve(i);
printf("%.3lf %.3lf %.3lf",ansxor,ansand,ansor);
return 0;
}
低价购买
——因为这个题要输出不同种的方案数
题目要求是“它们构成的价格队列不一样”,那么我准备拿一个数组存下这个最长下降子序列,但是这不现实,检查是否匹配是在最坏的情况下可能达到Θ(N^3)Θ(N3)。
于是有了现在的解法,让我来简单证明说明一下
在dpdp过程中,ff数组存的是最长下降子序列的长度,ff数组的下标ii是以ii结尾的意思,所以最长下降子序列(除了最后一位外)的数据已经丢失,因此不能在方案数相加时再判断是否能加。
我们从头来看,
- 如果一个数列的第一个数与另一个数列的第一个数相同,那么现在可以判断它们相等,即可以把其中一个删掉(在代码中的处理是t[i]=0t[i]=0)。当不同的数接在它的后面时,又可以将它们判断为两个数列,这是不互相影响的。因为两个数列都可以由这个相等的数列转移而来
- 如果一个数列的第一个数与另一个数列的第一个数不同,那么它们不等,且无论后面添加什么,都不相等,即不删去,则按照普通的判断继续做。
由上面的两点,我们已经把重复的删掉,这样可以防止重复计数。
tiptip:本题如果出现在考试中,请不要冒险定义int,因为maxint是2^{31}-1231−1,会爆int,这个题暂不做深究
Code:
#include<cstdio>
#include<cstring>
int max(int x,int y){return x>y?x:y;}
int a[5001],f[5001],t[5001];
//a[i]存的是第i天股票的价格
//f[i]存的是第i天最长下降子序列的长度
//t[i]存的是以i结尾的最长下降子序列的种类(方案)
int main()
{
memset(f,0,sizeof(f));//初始化长度
memset(t,0,sizeof(t));//初始化方案
int n,maxx=0;
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
{
for(int j=1;j<i;j++)
if(a[i]<a[j])//延长已经存在的最长下降子序列
f[i]=max(f[i],f[j]+1);
if(f[i]==0)
f[i]++;//如果当前的数是目前为止最大的,则最长下降子序列是自己
if(f[i]>maxx)
maxx=f[i];//在f数组更新完毕后,存下最长下降子序列的长度
for(int j=1;j<i;j++)
if(f[i]==f[j]&&a[i]==a[j])
t[j]=0;//如果与前面的数列相同,则舍去前面的数列,防止重复计数
else if(f[i]==f[j]+1&&a[i]<a[j])
t[i]+=t[j];//如果可以接上前面的数列,则继承其方案数
if(!t[i])//如果当前的数是目前为止最大的,则是初始方案
t[i]=1;
}
int sum=0;//sum计数,用于存最长下降子序列(方案)的个数
for(int i=1;i<=n;i++)
if(f[i]==maxx)
sum+=t[i];
printf("%d %d",maxx,sum);
return 0;
}
彩票
不知道这道HNOI的题为什么没人发题解~~(是太水了么)~~
先说一下题意:很显然,题意要求从m个自然数中选择n个使得倒数之和为x/y,输出满足条件的方案数。(m<=50,n<=10)
数据范围就一定说明了很多,显然就是一个搜索剪枝。最基本的剪枝就是如果比x/y大就返回。还有两个剪枝就比较常见了。1.如果当前的值加上最大可能的值小于答案那就返回;2.如果当前的值加上最小可能的值大于答案那就返回。我抱着试一试的想法,然后就A了。不过肯定还有更多的剪枝,但是这样已经能过。
下附代码:
#include<bits/stdc++.h>
using namespace std;
inline void read(int &x)
{
x=0;
static int p;p=1;
static char c;c=getchar();
while(!isdigit(c)){if(c=='-')p=-1;c=getchar();}
while(isdigit(c)) {x=(x<<1)+(x<<3)+(c-48);c=getchar();}
x*=p;
}
const double eps=1e-10;
int n,m,x,y,ans;
double tag;
bool vis[60];
void dfs(int x,double sum,int last)
{
if(sum-tag>eps)return;
if(sum+(double)(n-x+1)*1.0/(double)(last+1)+eps<tag)return;
if((sum+(double)(n-x+1)*1.0/(double)m)>tag+eps)return;
if(x==n+1)
{
if(fabs(sum-tag)<=eps)ans++;
return ;
}
for(int i=last+1;i<=m;i++)
{
if(!vis[i])
{
vis[i]=true;
dfs(x+1,sum+1.0/(double)i,i);
vis[i]=false;
}
}
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
read(n);read(m);read(x);read(y);
tag=(double)x/(double)y;
dfs(1,0,0);
cout<<ans<<endl;
return 0;
}
定价
看L和R的范围,显然不能一个一个加,这样会有很多重复情况,会超时,只要看该数有多少个后导0,就把L加上10的多少次方。
很容易可以想到价格后面尽可能多0,在此基础上需要尽量最后一个数字是5。 那么我们可以想到每次更新的时候尽量跳10^N。
用一重while循环,从L开始往R找,因为题目要输出最小的一个值,还有当ANS为1是,代码会跑的飞快,嘿嘿~
我的代码短,希望能通过审核~
#include <bits/stdc++.h>
using namespace std;
long long l,r,T;
long long mn=999999999999,ans;
int main()
{
freopen("price.in","r",stdin);
freopen("price.out","w",stdout);
cin>>T;
while (T--) {
scanf("%lld%lld",&l,&r);
while (l<=r) {
long long x=l,cnt=0;
while (x%10==0) x/=10,++cnt;
long long y=x,len=0,f=x%10;
while (y) y/=10,++len;
long long p=0;
if (f==5) --p;
p+=2*len;
if (mn>p) mn=p,ans=l;
l+=pow(10,cnt);
}
printf("%lld\n",ans);
mn=999999999999;
}
return 0;
}边栏推荐
猜你喜欢

系统基础-学习笔记(一些命令记录)
淘宝客APP带自营商城本地生活CPS外卖优惠电影票话费更新渠道跟单生活特权V3
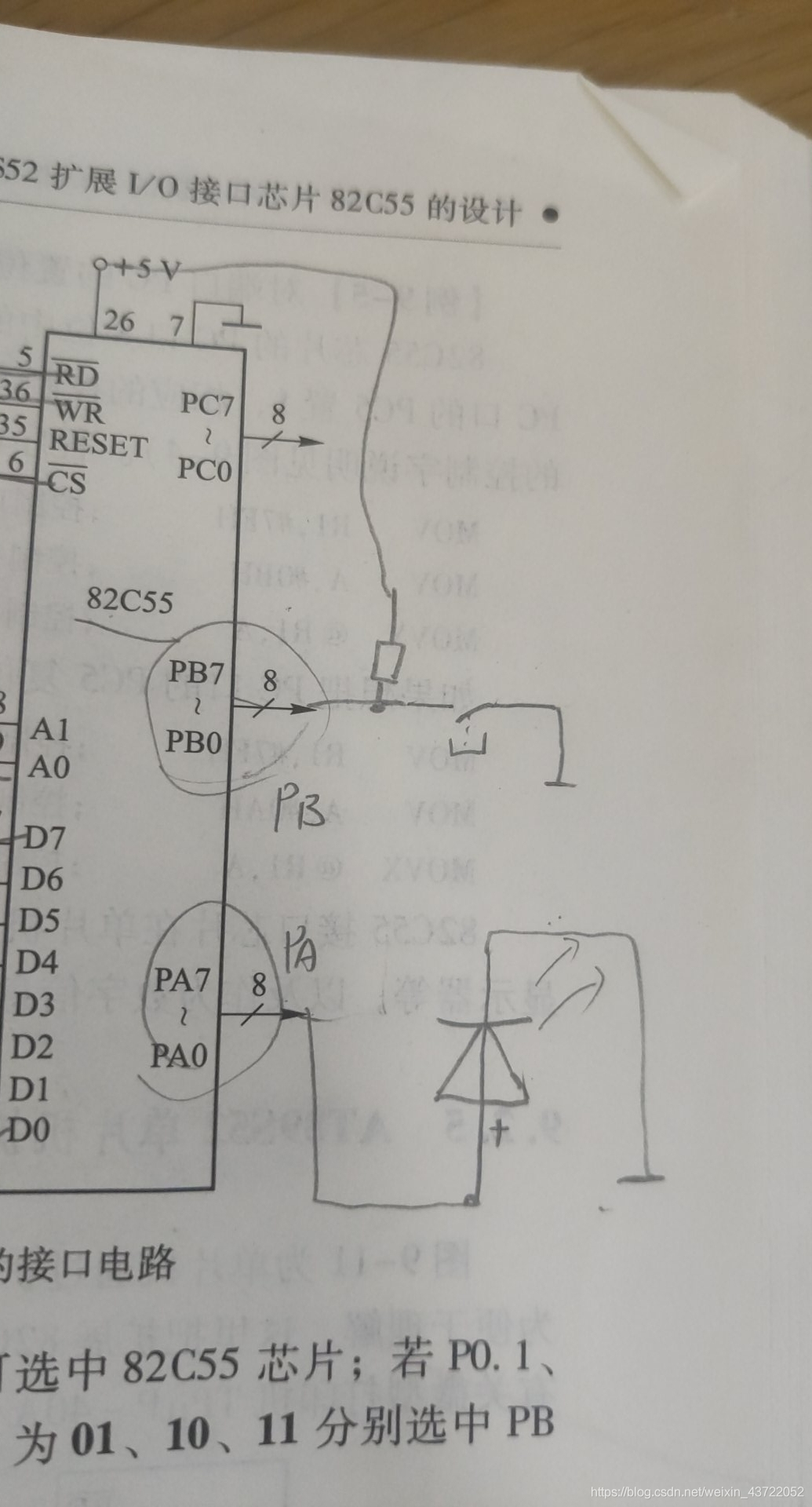
单片机期末复习大题
LaTeX uses frame to make PPT pictures without labels
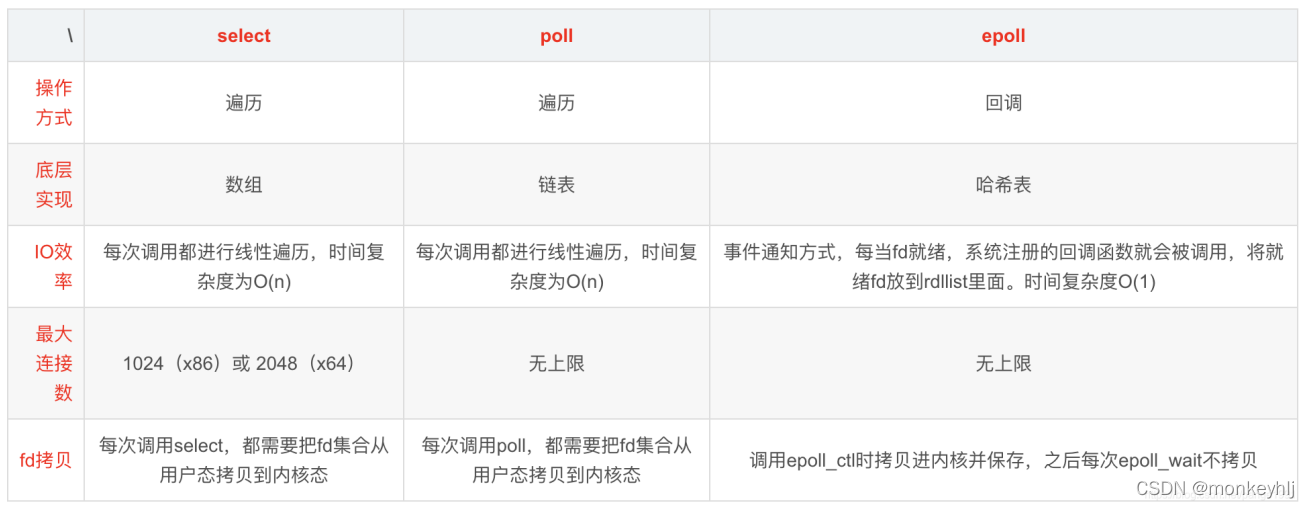
BIO,NIO,AIO实践学习笔记(便于理解理论)
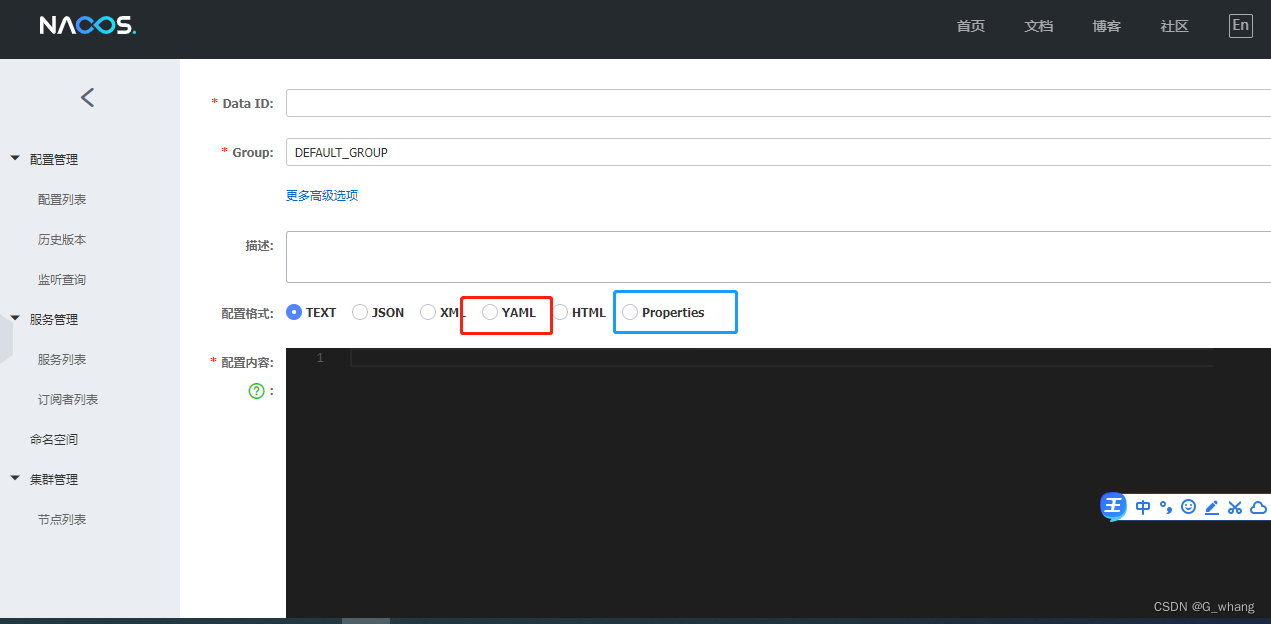
NACOS配置中心设置配置文件
Configuration of routers and static routes

人人AI(吴恩达系列)
D45_Camera assembly Camera
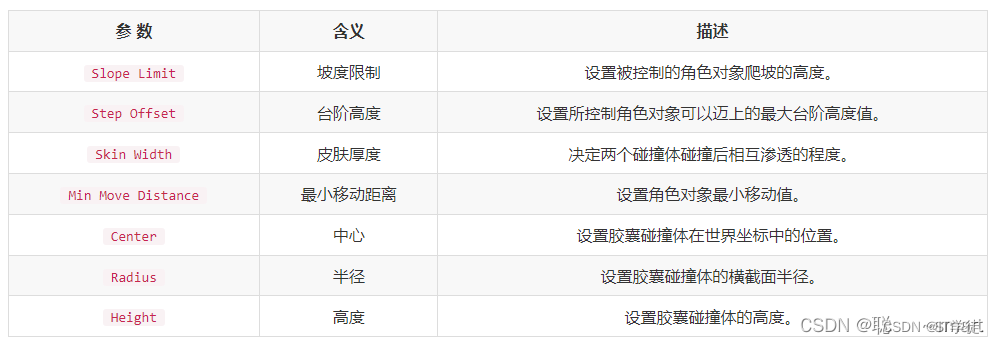
Collision, character controller, Cloth components (cloth), joints in the Unity physics engine
随机推荐
Transformer interprets and predicts instance records in detail
Come, come, let you understand how Cocos Creator reads and writes JSON files
字体样式及其分类
边缘盒子+时序数据库,美的数字化平台 iBUILDING 背后的技术选型
Late night drinking, 50 classic SQL questions, really fragrant~
unity 将Text批量替换为TextMeshProUGUI
Browser Storage for H5
Drools规则引擎快速入门(一)
Cloud Computing Basics - Study Notes
盒子模型大详解
LaTeX image captioning text column automatic line wrapping
Q 2020, the latest senior interview Laya soul, do you know?
Configuration of routers and static routes
js 使用雪花id生成随机id
Some basic method records of commonly used languages in LeetCode
自营商城提高用户留存小技巧,商城对接小游戏分享
document.querySelector() method
D39_Eulerian Angles and Quaternions
export使用
sql server duplicate values are counted after
