lingo入门——河北省第三届研究生建模竞赛B题

一、题干

1.1 题目

投资建模(河北省第三届研究生建模竞赛B题)
        从2021年年初开始到2050年前，未来教育基金会（FFE）向M国部分高等院校捐助一笔经费以帮助贫困学生，将现有的8000万美元资金进行债务投资。
相关投资要求：

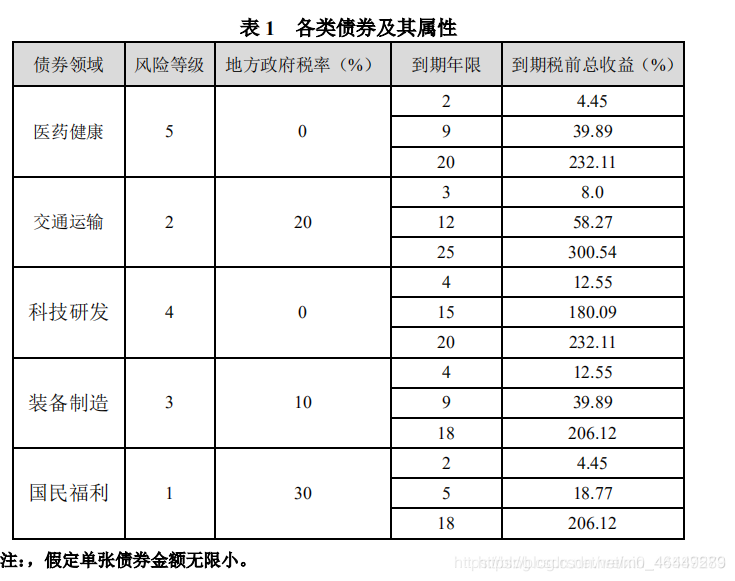
1. 医药健康债券购买金额不能少于购买总金额的20%，交通运输、科技研发、装备制造以及国民福利的债券购买金额不能少于购买总金额的10%。
2. 所购买债券的平均风险等级不得低于2.5，等级数字越大，风险越低。
3. 所购买的债券的平均到期年限不超过10年。
4. 要求捐助活动结束后FFE继续保留8000万美元资金。

        如上所示为各个基金的一些信息，值得注意的是，其对风险等级的约束很小，而收益率又定义为固定值，所以这个模型相对实际问题已经做了很大的简化。

1.2 问题

• 若 SEB 债券投资只允许在第一年初进行，分配8000万美元使收益最大。
• 假定可以进行重复投资，使得 2050 年末的一次性捐款金额达到最大。
• FFE 改变捐助方式，计划从 2021 开始，在未来 30 年内每年年初捐助一笔每年金额固定的经费。允许重复投资。使得每年捐助的金额达到最大。
• FFE 为了帮助疫情防控，决定在每年捐助给高校的金额尽量不低于第 3 问 的金额的前提下，投资尽量向医药健康和科技研发上倾斜。原则上规定：医药健康的投资额，尽量与科技研发相等，尽量是交通运输的 1.2 倍，尽量是装备制造 的 1.5 倍，尽量是国民福利的 2 倍。允许重复投资。
  

二、模型的建立

        第一问没啥写的价值，直接写第二、三、四问。

2.1 符号

符号	意义
$money\_i{n}_i$	第$i$年在收入状态后的总资金
$money\_ou{t}_i$	第$i$年在支出状态后的总资金
$x_{i,j}$	第$i$年对第$j$个债券的购买量
$a_i$	第$i$个产品在一轮周期后的利润率
$b_i$	第$i$个产品一轮周期时常
$c_i$	第$i$个产品增值税率
$d_i$	第$i$个产品风险等级
$p$	每年的捐款数量

2.2、思路

2.2.1、思路1

        观察这道题目在投资时的资金流转过程，可以发现它每年都有这么两组操作：

• 继承一年剩下的资产、获取前几年投资所带来的利润
• 进行各类债券进行投资、对外捐赠（第三问）

        所以我们可以考虑对该问约束时进行状态分离，即先进行$moneyi{n}_i$操作，再进行$moneyou{t}_i$操作。其间的等量关系大致如下，其他的具体情况在正式做的时候再具体讨论：
$$\begin{gathered} money\_i{n}_i=money\_ou{t}_{i-1}+\sum _{j=1}^{15}[x_{i-b_i,j}+x_{i-b_i,j}{a}_i(1-c_i)] \\ money\_i{n}_i=money\_ou{t}_i+p+\sum _{j=1}^{15}{x}_{i,j} \end{gathered}$$

2.2.2、思路2

        首先根据一个很明显的构想：如果你当下有钱，且时间足够充裕到你得到收益，那么你必然会去拿这笔钱去投资。甭管投啥，反正会投（而投啥其实就是我们要去求解的内容）。因为如果你今年不投，今后再投的话，在收益上除了时间线的后移外没有任何变化。所以这里本质上是一个带约束的贪心问题。
        我们可以粗略的建立一个等量关系，其他的具体情况在正式做的时候再具体讨论：
$$\sum _{j=1}^{15}{x}_{i,j}=\sum _{j=1}^{15}[x_{i-b_i,j}+x_{i-b_i,j}{a}_i(1-c_i)]$$

2.3 确定等量关系

        思考了上面两个思路后，发现他们本身其实是并不冲突的，但问题在于以上的贪心算法并没有考虑留每天的捐款的情况。只是表现的形式不一样。所以可以将他们结合起来，建立如下等量关系。
$$\{\begin{array}{l}money\_i{n}_i=money\_ou{t}_{i-1}+\sum _{j=1}^{15}[x_{i-b_i,j}+x_{i-b_i,j}{a}_i(1-c_i)]\\ money\_i{n}_i=money\_ou{t}_i+p+\sum _{j=1}^{15}{x}_{i,j}\end{array}$$
        然后基于我们对于题目的分析与各类情况的思考，可以得到以下几点：

• 当剩余天数少于该债券周期的话，那么必然不买这个债券。
• 因为债券最小周期为2天，且采用贪心策略，所以前两天必定是全部花费。（在第三问及第四问中，应留下用于每天捐赠的钱）
• 因为是贪心策略，所以$money\_ou{t}_i$只有在最后一天不为0（该特性为第二问独有，第三问与第四问需考虑给捐款存钱的情况）

将其转化为符号语言即为：
$$\{\begin{array}{l}\sum _{j=1}^{15}\sum _{i=31-b_j}^{30}{x}_{i,j}=0\\ \sum _{j=1}^{15}{x}_{1,j}+x_{2,j}=2p\end{array}$$

2.4、明确约束

        首先根据常识，可以得到如下几条约束：
$$\{\begin{array}{l}{x}_{i,j}>=0\\ p>=0\\ money\_i{n}_i>=money\_ou{t}_i>=0\end{array}$$
        然后根据那四条投资要求，可得出以下四个约束：
$$\{\begin{array}{l}\sum _{j=1}^{15}(b_j\sum _{i=1}^{30}{x}_{i,j})\le 10\sum _{j=1}^{15}\sum _{i=1}^{30}{x}_{i,j}\\ \sum _{j=1}^{15}(d_j\sum _{i=1}^{30}{x}_{i,j})\ge 2.5\sum _{j=1}^{15}\sum _{i=1}^{30}{x}_{i,j}\\ \sum _{i=1}^{30}(x_{i,1}+x_{i,2}+x_{i,3})>0.2\sum _{j=1}^{15}\sum _{i=1}^{30}{x}_{i,j}\\ \sum _{i=1}^{30}(x_{i,3k}+x_{i,3k-1}+x_{k,3j-2})>0.1\sum _{j=1}^{15}\sum _{i=1}^{30}{x}_{i,j}，(k\in \{2,3,4,5\})\end{array}$$
        暂时想到这些。

三、编写程序

3.1、第二问

3.2、第三问

3.3、第四问

四、总结