当前位置:网站首页>二叉树(Binary Tree)
二叉树(Binary Tree)
2022-07-07 21:50:00 【Yake1965】
二叉树(Binary Tree)
- 二叉搜索树
- [501. 二叉搜索树中的众数](https://leetcode.cn/problems/find-mode-in-binary-search-tree/)
- [剑指 Offer 54. 二叉搜索树的第k大节点](https://leetcode.cn/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof/)
- [剑指 Offer 36. 二叉搜索树与双向链表](https://leetcode.cn/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof/)
- [96. 不同的二叉搜索树](https://leetcode.cn/problems/unique-binary-search-trees/)
- [95. 不同的二叉搜索树 II](https://leetcode.cn/problems/unique-binary-search-trees-ii/)
- [剑指 Offer 34. 二叉树中和为某一值的路径](https://leetcode.cn/problems/er-cha-shu-zhong-he-wei-mou-yi-zhi-de-lu-jing-lcof/)
- [1609. 奇偶树](https://leetcode-cn.com/problems/even-odd-tree/)
- 1609. 奇偶树
- 100. 相同的树
- 101. 对称二叉树
- 104. 二叉树的最大深度
- 108. 将有序数组转换为二叉搜索树
- 110. 平衡二叉树
- 111. 二叉树的最小深度
- 230. 二叉搜索树中第K小的元素
- 559. N 叉树的最大深度
- 563. 二叉树的坡度
- 671. 二叉树中第二小的节点
- 700. 二叉搜索树中的搜索
- 863. 二叉树中所有距离为 K 的结点
- 1104. 二叉树寻路
- 二叉树路径
- 112. 路径总和
- 113. 路径总和 II
- 257. 二叉树的所有路径
- 437. 路径总和 III
- 988. 从叶结点开始的最小字符串
二叉搜索树
501. 二叉搜索树中的众数
二叉搜索树的中序遍历序列是一个非递减的有序序列,相同的数一定是连续的。
class Solution {
List<Integer> ans = new ArrayList<>();
int base, cnt, max;
public int[] findMode(TreeNode root) {
dfs(root);
int[] res = new int[ans.size()];
for(int i = 0; i < ans.size(); i++) res[i] = ans.get(i);
return res;
}
void dfs(TreeNode node){
if(node == null) return;
dfs(node.left);
update(node.val);
dfs(node.right);
}
void update(int x){
if(x == base) cnt++;
else {
cnt = 1;
base = x;
}
if(cnt == max) ans.add(base);
else if(cnt > max){
max = cnt;
ans.clear();
ans.add(base);
}
}
}
用 Morris 中序遍历的方法把中序遍历的空间复杂度优化到 O(1)。
剑指 Offer 54. 二叉搜索树的第k大节点
二叉搜索树的中序遍历为 递增序列,也就是 中序遍历倒序 为 递减序列 。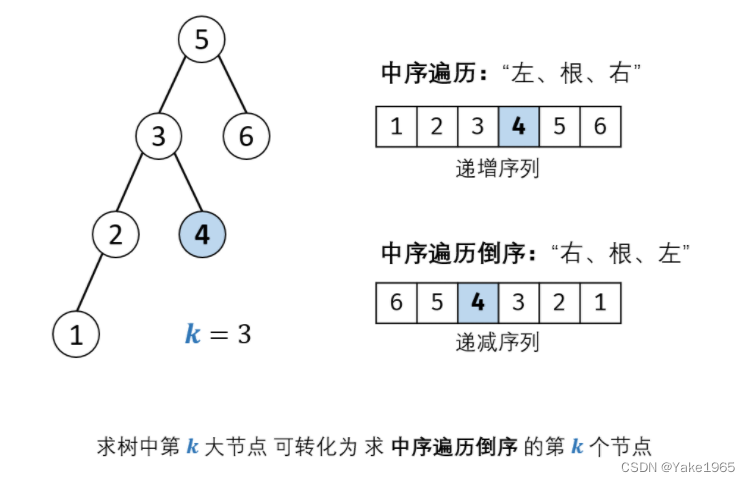
class Solution {
int k, ans = 0;
public int kthLargest(TreeNode root, int k) {
this.k = k;
dfs(root);
return ans;
}
void dfs(TreeNode root) {
if(root == null) return;
dfs(root.right);
if(--k == 0) {
ans = root.val; return;
}
dfs(root.left);
}
}
class Solution {
public int kthLargest(TreeNode root, int k) {
Deque<TreeNode> q = new ArrayDeque<>();
// while(q.size() > 0 || root != null){
while(true){
while(root != null){
q.push(root);
root = root.right;
}
root = q.pop();
if(--k == 0) return root.val;
root = root.left;
}
// return 0;
}
}
剑指 Offer 36. 二叉搜索树与双向链表
class Solution {
Node pre, head;
public Node treeToDoublyList(Node root) {
if(root == null) return null;
dfs(root);
head.left = pre;
pre.right = head;
return head;
}
void dfs(Node cur){
if(cur == null) return;
dfs(cur.left);
if(pre != null) pre.right = cur;
else head = cur;
cur.left = pre;
pre = cur;
dfs(cur.right);
}
}
96. 不同的二叉搜索树
class Solution {
int[] a = new int[20]; // a[0] = 1; a[1] = 1;
public int numTrees(int n) {
if(n == 0 || n == 1) return 1; // 左右相乘需要 t[0] = 1
if(a[n] > 0) return a[n];
int cnt = 0;
for (int i = 1; i <= n; i++) {
// 以 i 为根递归左右,相乘。
int left = numTrees(i-1);
int right = numTrees(n-i);
cnt += left * right;
}
a[n] = cnt;
return cnt;
}
}
95. 不同的二叉搜索树 II
class Solution {
public List<TreeNode> generateTrees(int n) {
return f(1, n);
}
List<TreeNode> f(int s, int e){
List<TreeNode> ans = new LinkedList();
if(s > e){
ans.add(null);
return ans;
}
for(int i = s; i <= e; i++){
List<TreeNode> left = f(s, i - 1);
List<TreeNode> right = f(i + 1, e);
for(TreeNode l : left){
for(TreeNode r : right){
TreeNode cur = new TreeNode(i);
cur.left = l;
cur.right = r;
ans.add(cur);
}
}
}
return ans;
}
}
剑指 Offer 34. 二叉树中和为某一值的路径
class Solution {
List<List<Integer>> ans = new LinkedList<>();
Deque<Integer> path = new ArrayDeque<>();
public List<List<Integer>> pathSum(TreeNode root, int target) {
dfs(root, target);
return ans;
}
void dfs(TreeNode root, int target){
if(root == null) return;
path.add(root.val);
target -= root.val;
if(root.left == null && root.right == null && target == 0){
ans.add(new LinkedList<Integer>(path));
}
dfs(root.left, target);
dfs(root.right, target);
path.pollLast();
}
}
1609. 奇偶树
class Solution {
public boolean isEvenOddTree(TreeNode root) {
Deque<TreeNode> q = new LinkedList<>();
q.offer(root);
boolean even = true;
while(!q.isEmpty()){
int size = q.size(), pre = (even) ? 0 : 1000000;
// for(int i = 0; i < q.size(); i++){ // 不能直接使用 q.size()
while(size-- > 0){
TreeNode node = q.poll();
int x = node.val;
if(even){
// 偶数下标,x 是偶数或递减
if(x % 2 == 0 || pre >= x) return false;
}
else{
// 奇数下标,x 是奇数或递增
if(x % 2 == 1 || pre <= x) return false;
}
pre = x;
if(node.left != null) q.offer(node.left);
if(node.right != null) q.offer(node.right);
}
even = !even;
}
return true;
}
}
1609. 奇偶树
class Solution:
def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:
q = deque([root])
even = True
while q:
pre = 0 if even else 1000000
for i in range(len(q)):
node = q.popleft()
x = node.val
if even:
if not x % 2 or x <= pre: return False
else:
if x % 2 or x >= pre: return False
pre = x
node.left and q.append(node.left)
node.right and q.append(node.right)
even = not even
return True
100. 相同的树
class Solution:
def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
if not p and not q: return True
if not p or not q or p.val != q.val: return False
# return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
# 中序
stackP, stackQ, curP, curQ = [p], [q], p.left, q.left
while stackP or stackQ or curP or curQ:
if not curP and curQ or curP and not curQ: return False
while curP and curQ:
stackP.append(curP)
stackQ.append(curQ)
curP = curP.left
curQ = curQ.left
curP = stackP.pop()
curQ = stackQ.pop()
if curP.val != curQ.val:
return False
curP = curP.right
curQ = curQ.right
return True
101. 对称二叉树
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
# q = [root, root]
q = [(root, root)]
while q:
# u = q.pop()
# v = q.pop()
u, v = q.pop()
if not u and not v: continue
if not u or not v or u.val != v.val:
return False
# q.extend([u.left, v.right])
# q.extend([u.right, v.left])
q.append((u.left, v.right))
q.append((u.right, v.left))
return True
104. 二叉树的最大深度
Leetcode
二叉树结点的深度: 指从根结点到该节点的最长简单路径 边 的条数。
二叉树结点的高度: 指从该结点到叶子节点的最长简单路径 边 的条数。
说明:leetcode 定义用结点为一度,根节点深度是 1;维基百科 定义用边为一度,根节点的深度是 0。
求深度可以从上到下去查,所以需要前序遍历(中左右),而高度只能从下到上去查,所以只能后序遍历(左右中)。
前序遍历
class Solution:
def maxDepth(self, root: TreeNode) -> int:
def getDepth(node, depth):
nonlocal result
result = max(depth, result) # 中
node.left and getDepth(node.left, depth + 1) # 左
node.right and getDepth(node.right, depth + 1) # 右
result = 0
if not root: return 0
getDepth(root, 1)
return result
二叉树的最大深度,也就是根节点的高度,所以也可以使用后序遍历。
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root: return 0
## bfs deque
# que = collections.deque([(root, 1)])
# while que:
# node, depth = que.popleft()
# res = depth # max(res, depth)
# node.left and que.append((node.left, depth + 1))
# node.right and que.append((node.right, depth + 1))
# return res # 不需要变量 res,直接返回 depth 即可。
## bfs list
q = [root]
res = 0
while q:
q = [child for node in q for child in [node.left, node.right] if child]
res += 1
return res
## dfs
# return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1
# return max(self.maxDepth(node) for node in [root.left, root.right]) + 1
108. 将有序数组转换为二叉搜索树
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
if not nums: return None
mid = len(nums) // 2 # 选中间的值
root = TreeNode(nums[mid])
if mid >= 1:
root.left = self.sortedArrayToBST(nums[:mid])
if mid < len(nums) - 1:
root.right = self.sortedArrayToBST(nums[mid+1:])
return root
110. 平衡二叉树
Leetcode
平衡二叉树:一个二叉树每个结点 的左右两个子树的高度差的绝对值不超过 1 。
方法一:自顶向下的递归
class Solution:
def isBalanced(self, root: TreeNode) -> bool:
# 子树的最大高度
def height(root: TreeNode) -> int:
return max(height(root.left), height(root.right)) + 1 if root else 0
return not root or abs(height(root.left) - height(root.right)) <= 1 and self.isBalanced(root.left) and self.isBalanced(root.right)
方法二:自底向上的递归
class Solution:
def isBalanced(self, root: TreeNode) -> bool:
def height(root: TreeNode) -> int:
if not root: return 0
left = height(root.left)
right = height(root.right)
return -1 if left == -1 or right == -1 or abs(left - right) > 1 else max(left, right) + 1
return height(root) >= 0
111. 二叉树的最小深度
方法一:深度优先搜索
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root: return 0
if not root.left and not root.right: return 1
min_depth = 10**9
if root.left:
min_depth = min(self.minDepth(root.left), min_depth)
if root.right:
min_depth = min(self.minDepth(root.right), min_depth)
return min_depth + 1
方法二:广度优先搜索
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root: return 0
que = collections.deque([(root, 1)])
while que:
node, depth = que.popleft()
if not node.left and not node.right: # 叶子结点
return depth
node.left and que.append((node.left, depth + 1))
node.right and que.append((node.right, depth + 1))
230. 二叉搜索树中第K小的元素
方法一:中序遍历
二叉搜索树:
- 结点的左子树只包含小于当前结点的数。
- 结点的右子树只包含大于当前结点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
中序遍历:
按照访问左子树—根结点—右子树的方式遍历二叉树;在访问其左子树和右子树时,也按照同样的方式遍历;直到遍历完整棵树。
「二叉树的中序遍历」参考**「94. 二叉树的中序遍历的官方题解」**
使用迭代方法,这样可以在找到答案后停止,不需要遍历整棵树。
class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
stack = []
while root or stack:
while root:
stack.append(root)
root = root.left
root = stack.pop()
k -= 1
if k == 0:
return root.val
root = root.right
方法二:记录子树的结点数
记录下以每个结点为根结点的子树的结点数,直接查找第 k 小的值。
class Bst:
def __init__(self, root: TreeNode):
self.root = root
# 统计以每个结点为根结点的子树的结点数,并存储在哈希表中
self._node_num = {
}
self._count_node_num(root)
def kth_smallest(self, k: int):
"""返回二叉搜索树中第k小的元素"""
node = self.root
while node:
left = self._get_node_num(node.left)
if left < k - 1: # 左树不够加右树
node = node.right
k -= left + 1
elif left == k - 1: # 左树正好差一,返回结点值。
return node.val
else:
node = node.left # 继续左树
def _count_node_num(self, node) -> int:
"""统计以node为根结点的子树的结点数"""
if not node:
return 0
self._node_num[node] = 1 + self._count_node_num(node.left) + self._count_node_num(node.right)
return self._node_num[node]
def _get_node_num(self, node) -> int:
"""获取以node为根结点的子树的结点数"""
return self._node_num[node] if node is not None else 0
# node is not None 不同于 not node 因为 node 可能为 null
class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
bst = Bst(root)
return bst.kth_smallest(k)
方法三:平衡二叉搜索树(AVL树)
平衡二叉搜索树:
- 平衡二叉搜索树中每个结点的左子树和右子树的高度最多相差 1;
- 平衡二叉搜索树的子树也是平衡二叉搜索树;
一棵存有 n 个结点的平衡二叉搜索树的高度是 O(logn)。
方法二中搜索二叉搜索树的时间复杂度为 O(H),其中 H 是树的高度;当树是平衡树时,时间复杂度取得最小值 O(logN)。因此,在记录子树的结点数的基础上,将二叉搜索树转换为平衡二叉搜索树,并在插入和删除操作中维护它的平衡状态。
其中,将二叉搜索树转换为平衡二叉搜索树,可以参考**「1382. 将二叉搜索树变平衡的官方题解」**。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class AVL:
"""平衡二叉搜索树(AVL树):允许重复值"""
class Node:
"""平衡二叉搜索树结点"""
__slots__ = ("val", "parent", "left", "right", "size", "height")
def __init__(self, val, parent=None, left=None, right=None):
self.val = val
self.parent = parent
self.left = left
self.right = right
self.height = 0 # 结点高度:以 node 为根节点的子树的高度(高度定义:叶结点的高度是 0)
self.size = 1 # 结点元素数:以 node 为根节点的子树的节点总数
def __init__(self, vals):
self.root = self._build(vals, 0, len(vals) - 1, None) if vals else None
def _build(self, vals, l, r, parent):
"""根据vals[l:r]构造平衡二叉搜索树 -> 返回根结点"""
m = (l + r) // 2
node = self.Node(vals[m], parent=parent)
if l <= m - 1:
node.left = self._build(vals, l, m - 1, parent=node)
if m + 1 <= r:
node.right = self._build(vals, m + 1, r, parent=node)
self._recompute(node)
return node
def kth_smallest(self, k: int) -> int:
"""返回二叉搜索树中第k小的元素"""
node = self.root
while node:
left = self._get_size(node.left)
if left < k - 1:
node = node.right
k -= left + 1
elif left == k - 1:
return node.val
else:
node = node.left
def insert(self, v):
"""插入值为v的新结点"""
if self.root is None:
self.root = self.Node(v)
else:
# 计算新结点的添加位置
node = self._subtree_search(self.root, v)
is_add_left = (v <= node.val) # 是否将新结点添加到node的左子结点
if node.val == v: # 如果值为v的结点已存在
if node.left: # 值为v的结点存在左子结点,则添加到其左子树的最右侧
node = self._subtree_last(node.left)
is_add_left = False
else: # 值为v的结点不存在左子结点,则添加到其左子结点
is_add_left = True
# 添加新结点
leaf = self.Node(v, parent=node)
if is_add_left:
node.left = leaf
else:
node.right = leaf
self._rebalance(leaf)
def delete(self, v) -> bool:
"""删除值为v的结点 -> 返回是否成功删除结点"""
if self.root is None:
return False
node = self._subtree_search(self.root, v)
if node.val != v: # 没有找到需要删除的结点
return False
# 处理当前结点既有左子树也有右子树的情况
# 若左子树比右子树高度低,则将当前结点替换为右子树最左侧的结点,并移除右子树最左侧的结点
# 若右子树比左子树高度低,则将当前结点替换为左子树最右侧的结点,并移除左子树最右侧的结点
if node.left and node.right:
if node.left.height <= node.right.height:
replacement = self._subtree_first(node.right)
else:
replacement = self._subtree_last(node.left)
node.val = replacement.val
node = replacement
parent = node.parent
self._delete(node)
self._rebalance(parent)
return True
def _delete(self, node):
"""删除结点p并用它的子结点代替它,结点p至多只能有1个子结点"""
if node.left and node.right:
raise ValueError('node has two children')
child = node.left if node.left else node.right
if child is not None:
child.parent = node.parent
if node is self.root:
self.root = child
else:
parent = node.parent
if node is parent.left:
parent.left = child
else:
parent.right = child
node.parent = node
def _subtree_search(self, node, v):
"""在以node为根结点的子树中搜索值为v的结点,如果没有值为v的结点,则返回值为v的结点应该在的位置的父结点"""
if node.val < v and node.right is not None:
return self._subtree_search(node.right, v)
elif node.val > v and node.left is not None:
return self._subtree_search(node.left, v)
else:
return node
def _recompute(self, node):
"""重新计算node结点的高度和元素数"""
node.height = 1 + max(self._get_height(node.left), self._get_height(node.right))
node.size = 1 + self._get_size(node.left) + self._get_size(node.right)
def _rebalance(self, node):
"""从node结点开始(含node结点)逐个向上重新平衡二叉树,并更新结点高度和元素数"""
while node is not None:
old_height, old_size = node.height, node.size
if not self._is_balanced(node):
node = self._restructure(self._tall_grandchild(node))
self._recompute(node.left)
self._recompute(node.right)
self._recompute(node)
if node.height == old_height and node.size == old_size:
node = None # 如果结点高度和元素数都没有变化则不需要再继续向上调整
else:
node = node.parent
def _is_balanced(self, node):
"""判断node结点是否平衡"""
return abs(self._get_height(node.left) - self._get_height(node.right)) <= 1
def _tall_child(self, node):
"""获取node结点更高的子树"""
if self._get_height(node.left) > self._get_height(node.right):
return node.left
else:
return node.right
def _tall_grandchild(self, node):
"""获取node结点更高的子树中的更高的子树"""
child = self._tall_child(node)
return self._tall_child(child)
@staticmethod
def _relink(parent, child, is_left):
"""重新连接父结点和子结点(子结点允许为空)"""
if is_left:
parent.left = child
else:
parent.right = child
if child is not None:
child.parent = parent
def _rotate(self, node):
"""旋转操作"""
parent = node.parent
grandparent = parent.parent
if grandparent is None:
self.root = node
node.parent = None
else:
self._relink(grandparent, node, parent == grandparent.left)
if node == parent.left:
self._relink(parent, node.right, True)
self._relink(node, parent, False)
else:
self._relink(parent, node.left, False)
self._relink(node, parent, True)
def _restructure(self, node):
"""trinode操作"""
parent = node.parent
grandparent = parent.parent
if (node == parent.right) == (parent == grandparent.right): # 处理需要一次旋转的情况
self._rotate(parent)
return parent
else: # 处理需要两次旋转的情况:第1次旋转后即成为需要一次旋转的情况
self._rotate(node)
self._rotate(node)
return node
@staticmethod
def _subtree_first(node):
"""返回以node为根结点的子树的第1个元素"""
while node.left is not None:
node = node.left
return node
@staticmethod
def _subtree_last(node):
"""返回以node为根结点的子树的最后1个元素"""
while node.right is not None:
node = node.right
return node
@staticmethod
def _get_height(node) -> int:
"""获取以node为根结点的子树的高度"""
return node.height if node is not None else 0
@staticmethod
def _get_size(node) -> int:
"""获取以node为根结点的子树的结点数"""
return node.size if node is not None else 0
class Solution:
def kthSmallest(self, root: TreeNode, k: int) -> int:
def inorder(node):
if node.left:
inorder(node.left)
inorder_lst.append(node.val)
if node.right:
inorder(node.right)
# 中序遍历生成数值列表
inorder_lst = []
inorder(root)
# 构造平衡二叉搜索树
avl = AVL(inorder_lst)
# 模拟1000次插入和删除操作
random_nums = [random.randint(0, 10001) for _ in range(1000)]
for num in random_nums:
avl.insert(num)
random.shuffle(random_nums) # 列表乱序
for num in random_nums:
avl.delete(num)
return avl.kth_smallest(k)
559. N 叉树的最大深度
class Solution:
def maxDepth(self, root: 'Node') -> int:
res = 0
if not root:return 0
q = [root]
while q:
q = [child for node in q for child in node.children]
res += 1
return res
# return max((self.maxDepth(child) for child in root.children), default=0) + 1 if root else 0
563. 二叉树的坡度
class Solution:
def __init__(self):
self.ans = 0
def findTilt(self, root: TreeNode) -> int:
# 返回 node 子树的和,同时累加坡度。
# 可以使用成员变量,也可以用 nonlocal。
def dfs(root):
if not root: return 0
sumLeft = dfs(root.left)
sumRight = dfs(root.right)
self.ans += abs(sumLeft - sumRight)
return sumLeft + sumRight + root.val
dfs(root)
return self.ans
671. 二叉树中第二小的节点
方法一:深度优先搜索
根节点的值是第一最小值。如果第二小的值不存在,则输出 -1,设初值 ans = -1。
假设当前节点为 node,如果 node.val > root.val,并且 ans = -1 (第一次)或者 node.val < ans,那么更新 ans。
此外,如果 node.val > ans,那么当前节点所有子节点的值都 >= ans,无需对该子树进行遍历。
最后遍历完整棵二叉树后,返回 ans。
class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
ans = -1
def dfs(node: TreeNode) -> None:
nonlocal ans
if not node or node.val >= ans > -1: return
if node.val > root.val: # ans 第一次更新 或 更小
ans = node.val
dfs(node.left)
dfs(node.right)
dfs(root)
return ans
用集合实现,判断更简单。
class Solution(object):
def findSecondMinimumValue(self, root: TreeNode)--> int:
res = set()
def dfs(node):
if not node: return
if node.val != root.val:
res.add(node.val)
return
dfs(node.left)
dfs(node.right)
dfs(root)
res = sorted(res)
return -1 if not res else res[0]
方法二:
思路很简单,如果节点不空,保存其值,左右节点不空,加入队列。
class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
s = set()
queue = [root]
while queue:
node = queue.pop()
if len(s)>1 and node.val >= sorted(s)[1]:continue # 优化:不符合条件的去掉
s.add(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return -1 if len(s) < 2 else sorted(s)[1]
进一步优化
class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
ans = -1
queue = [root]
while queue:
node = queue.pop()
# if len(s)>1 and node.val >= sorted(s)[1]:continue
if node.val >= ans > -1: continue
if node.val > root.val: # ans 第一次更新 或 更小
ans = node.val
continue
# if node.val > root.val:
# # ans 还未重新赋值(-1),直接赋值为 node.val 已赋值,取最小值
# ans = node.val if ans == -1 else min(ans, node.val)
# continue
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return ans
遍历二叉树
一棵二叉树由根结点 (val)、左子树 (left) 和右子树 (right) 三部分组成,若规定 M、L、R 分别代表 val、left、right,则二叉树的遍历方式有 6 种:
MLR - MRL - LMR - LRM - RDL - RLD
由于先遍历 left 和先遍历 right 在算法设计上没有本质区别,所以,仅看应用最广泛的 3 种(先左后右,比较符合咱们现在写字的顺序,利于理解)即可(dfs: 深度优化),当然除了这些方法,遍历方法还有层序遍历方法(bfs: 广度优先):
- MLR 前序遍历 : val -> left -> right
- LMR 中序遍历:left -> val -> right
- LRM 后序遍历:left -> right -> val
以上遍历方法,都可以由以下方法来实现:
- Recursive :递归
- Iteration : 迭代
- Morris : 以及为了解决以上实现方案中空间复杂度高的问题所衍生出的方法 ( Morris 遍历)
按递归(前) -> 迭代(中)-> Morris (中)顺序来实现
前序递归 val -> left -> right
class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
''' 根据题意: 一个节点的根是其所有子节点的最小值 因此根节点是二叉树中的最小值 '''
self.minValue = root.val
self.res = -1
# dfs -> preorder
self.preorder(root)
# 返回结果值
return self.res
''' dfs -> inorder @param node '''
def preorder(self, node: TreeNode) -> int:
# 当节点为空时,不需要任何处理
# 当 res 已赋值,且当前节点 val 大于 res 时,直接返回即可
if not node or node.val >= self.res > -1: return
# 当前值不等于最小值,且比之前的 res 要小,更新 res 值
if node.val > self.minValue: self.res = node.val
# 递归 left
self.preorder(node.left)
# 递归 right
self.preorder(node.right)
中序迭代 left -> val -> right
此方法与递归在时间,空间上来说没多大优势,但解决了递归深度如果过高时会栈溢出的风险。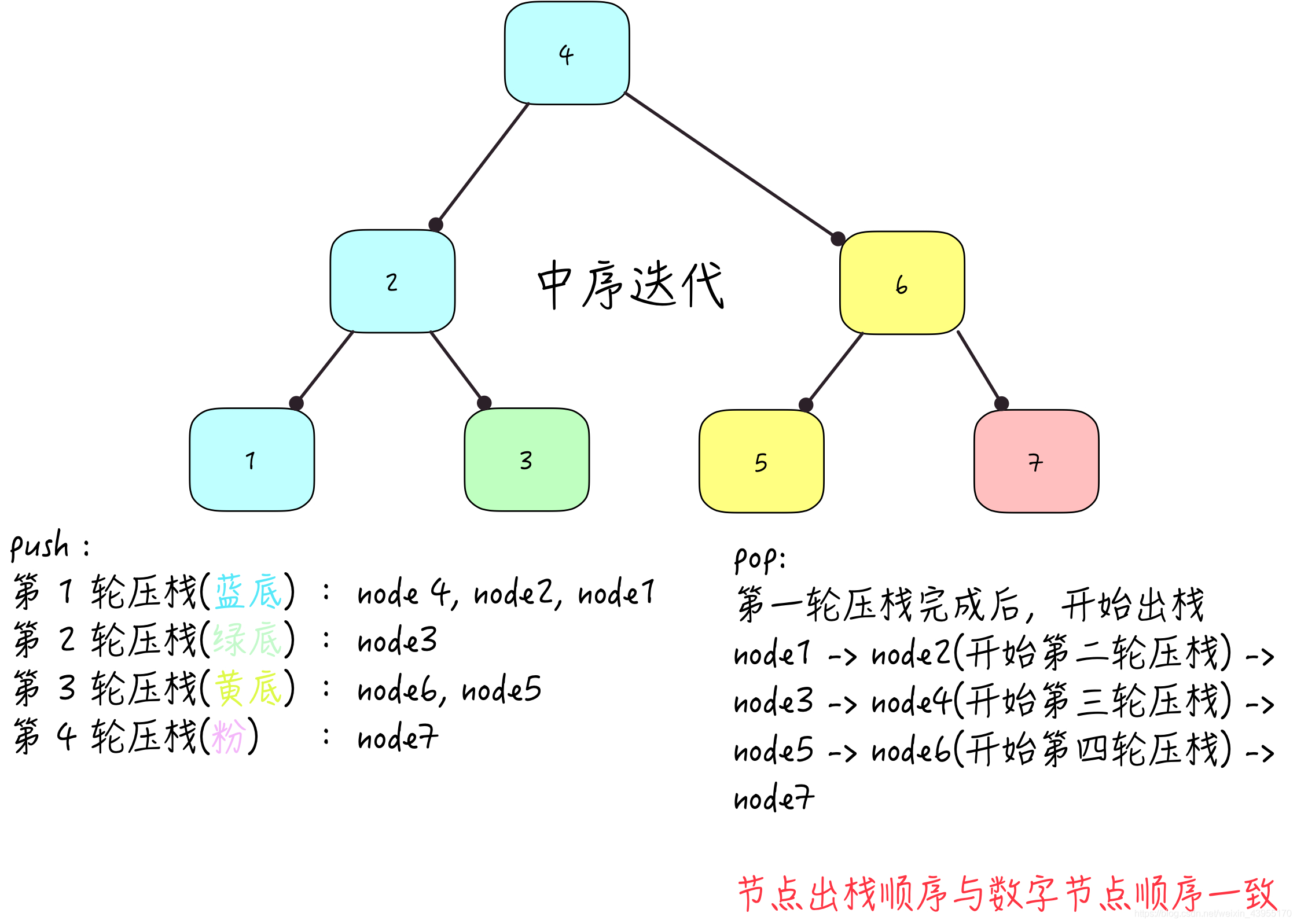
class Stack(object):
"""栈"""
def __init__(self): self.items = []
def isEmpty(self): return self.items == []
def push(self, item): self.items.append(item)
def pop(self): return self.items.pop()
class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
res, minValue = -1, root.val
help = Stack()
help.push(root) # 首先 root 压栈
# 中序遍历,首先遍历 left,定义当前节点为 root.left
cur = root.left
# 当前节点不为空或栈不为空时才进行压栈
while cur or not help.isEmpty():
# cur 不空入栈
while cur:
help.push(cur)
cur = cur.left
''' root < left < left ... None > left ... < right < left ... 每一轮 压栈完成后,cur 当前节点为空 将栈顶节点出栈 '''
cur = help.pop()
if cur.val > minValue:
# res 还未重新赋值(-1),直接赋值为 cur.val 已赋值,取最小值
res = cur.val if res == -1 else min(res, cur.val)
# 将栈顶节点出栈给 cur,如果 cur.right 不空进行下一轮入栈,如果为空继续出栈。
cur = cur.right
return res
中序 Morris
Morris 遍历跟上述两种方法不同点在于,不需要递归或者临时的栈空间来辅助完成中序遍历,空间复杂度: 常数级别, O(1)。
但是为了解决从 child 树 到 parent 树,需要临时修改树的结构,也就是说会失去树本身带来的数据结构优势,仅仅是为了完成遍历,所带来的缺陷,但不要着急,用完以后将指针还原即可
为了更好的理解原理需要当前 cur 和 临时 predecessor 2个指针, 具体步骤如下:
如果左子树节点为空, 将当前节点 val 添加到结果集 res 中(这里的 res 与代码中不大一样,这里的 res 是为了更好的理解
Morris 过程),cur 指向其右子树 right 节点 (cur = cur.right)如果左子树不为空, 遍历左子树的最右侧 right 子节点 (predecessor),在寻找的过程中会出现以下 2 种之一场景:
predecessor.right 为空时,将 right 指针指向 cur 节点, cur 指向其左子树节点 (cur = cur.leftcur=cur.left)
predecessor.right 不为空时, 表示原来的叶子节点连接已经存在(已经遍历完 cur.left)
- 将 predecessor.right = nullpredecessor.right=null
- cur 节点 val 添加到结果集 res 中 res.add(cur.val)res.add(cur.val)
- cur 指向 其 right 节点 (cur = cur.rightcur=cur.right)
重复以上 2 步直到 cur 节点为空
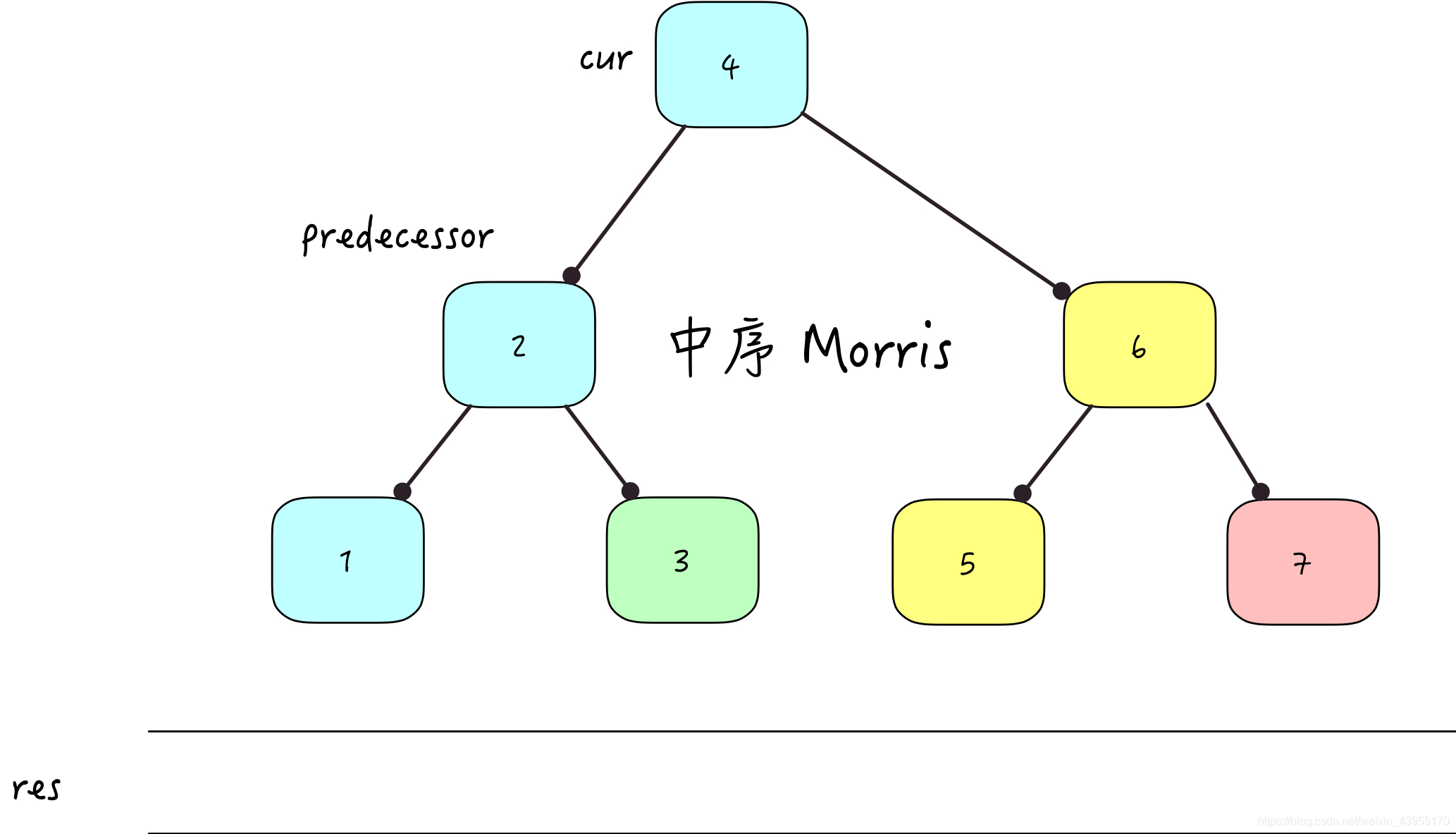
以上过程是为了更好的理解 Morris 遍历过程
此题: 根据以上 res 结果集,找出比 root.val 大的第二小值即可,具体过程看代码注释
class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
res, minValue = -1, root.val
cur = root
while cur:
# cur 左树为空,将其 val 进行判断,是否符合 res 的更新逻辑
# 符合条件将当前节点 val 更新到 res, , `cur` 指向其右子树 `right` 节点 (cur = cur.right)
if not cur.left:
if cur.val > minValue:
res = cur.val if res == -1 else min(res, cur.val)
cur = cur.right
else:
# 如果左子树不为空, 找 predecessor 节点
predecessor = cur.left
while predecessor.right and predecessor.right != cur:
predecessor = predecessor.right
# 下面对应描述中的 2 种场景
# predecessor.right 为空
if not predecessor.right:
# 将 predecessor.right 与 cur 建立链接
predecessor.right = cur
# 当前节点指向其 left 树
cur = cur.left
else:
if cur.val > minValue:
res = cur.val if res == -1 else min(res, cur.val)
predecessor.right = None
cur = cur.right
return res
700. 二叉搜索树中的搜索
class Solution:
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
## 方法一:for
cur = root
while cur:
if cur.val == val: return cur
cur = cur.left if cur.val > val else cur.right
return None
## 方法二:递归
if not root: return None
if root.val == val: return root
return self.searchBST(root.left if root.val > val else root.right, val)
863. 二叉树中所有距离为 K 的结点
方法一:深度优先搜索 + 哈希表
若将 target 当作树的根结点,从 target 出发,使用深度优先搜索与 target 距离为 k 的所有结点。
二叉树没有记录父结点,从根结点 root 出发,使用深度优先搜索遍历整棵树,同时用一个哈希表记录每个结点的父结点。结点值是唯一的,可以用结点值作为哈希表的键。
然后从 target 出发,使用深度优先搜索遍历整棵树,搜索左、右和父节点。
此外,为避免在深度优先搜索时重复访问结点,额外传入来源结点 frm。
class Solution:
def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:
# 所有节点的值对应父节点 pre = {node.val:preNode}
def findPre(node):
# if node.left:
# pre[node.left.val] = node
# findPre(node.left)
# if node.right:
# pre[node.right.val] = node
# findPre(node.right)
for n in [node.left,node.right]:
if n:
pre[n.val] = node
findPre(n)
def findAns(node, frm, depth, k):
if not node: return
if depth == k:
ans.append(node.val)
return
# if node.left != frm:
# findAns(node.left, node, depth + 1, k)
# if node.right != frm:
# findAns(node.right, node, depth + 1, k)
# if pre.get(node.val) != frm:
# findAns(pre.get(node.val), node, depth + 1, k)
# pre.get(node.val) 父节点
for n in [node.left, node.right, pre.get(node.val)]:
if n != frm:
findAns(n, node, depth + 1, k)
pre = {
} # key 节点的值:value 对应父节点
ans = []
# 从 root 出发 DFS,通过节点的值记录每个结点的父结点
findPre(root)
# 从 target 出发 DFS,寻找所有深度为 k 的结点
findAns(target, None, 0, k)
return ans
方法二:
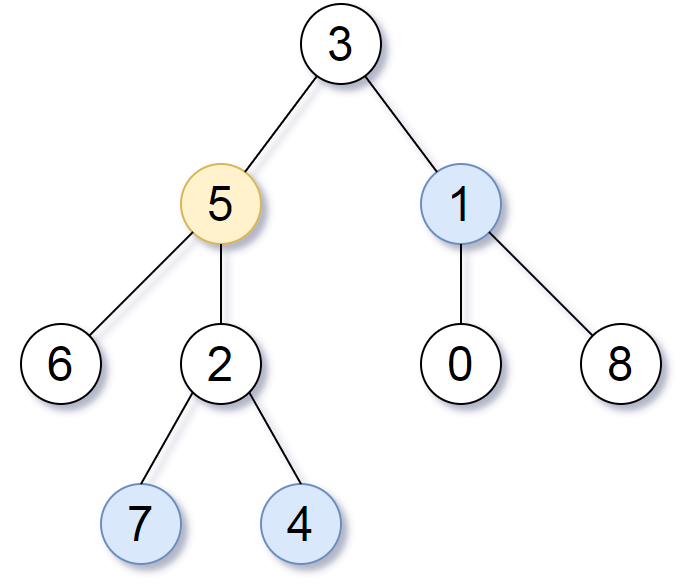
思路 分两种情况:
1、遍历任意节点的所有子节点 findNext()
如:5 => [6, 2, 7, 4] 7, 4 符合答案
3 => [1, 0, 8] 1 符合答案
2、遍历 5 所有父辈节点,只需要标记 target 的父辈节点。也就是 target 到 root 的路径。findPre()
在遍历父辈节点时,用上面 1 的方法遍历另外一个分支。
如:5 => 3
class Solution:
def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]:
# ⑵ 递归遍历 node 的子节点
def findNext(node, depth):
if not node: return
if depth == k:
res.append(node.val)
return
for n in [node.left, node.right]:
if n:
findNext(n, depth + 1)
# ⑶ 递归遍历 node 父辈节点,同时处理另一个分支,需要先标记父辈节点。
def findPre(node, depth):
# pre.get(node.val) 父节点 p
p = pre.get(node.val)
if not p: return # 只有 root.parents = None
if depth + 1 == k:
res.append(p.val)
return
# 用 findNext() 搜索父节点的另一个分支
for x in [p.left, p.right]:
if x != node: # 获取另一分支 node、x 是 p 的左右子节点。
findNext(x, depth + 2)
# 递归遍历 父节点
findPre(p, depth + 1)
res = [] # 符合条件的节点值
pre = {
} # key 节点值 : value 节点 target 到 root 路径
# ⑴ 只标记 k 父辈节点就可以了,实际标记的比较多。
# 也可以用递归的方法,这里用了 list。
help = [root]
pre[root] = None
while help:
node = help.pop()
for cur in [node.left, node.right]:
if cur:
pre[cur.val] = node
help.append(cur)
if cur == target:break # 如果找到 target 终止
findPre(target, 0)
findNext(target, 0)
return res
1104. 二叉树寻路
方法一:
从左到右的二叉树,父节点是子节点 // 2;
- 第 i 行有 2 i-1 个节点,节点标号为 2 i-1 至 2 i - 1;
- 对于标号为 x 的节点,当 x > 1 时,其父节点的标号为 x // 2 。
按一条龙,父节点是子节点对称节点 // 2。
- 每一行 的节点与对称节点标号之和都相等,如:15 ~ 8 节点 14 的对称节点是 15 + 8 - 14 = 9
class Solution:
def pathInZigZagTree(self, label: int) -> List[int]:
row = int(math.log(label,2)) + 1
ans = [0] * row
for i in range(row,0,-1):
ans[i-1] = label
label = (pow(2,i) - 1 - label + pow(2,i-1)) // 2
return ans
二叉树路径
深度优先搜索(DFS)和广度优先搜索(BFS)
左边是 BFS,按照层进行搜索;图右边是 DFS,先一路走到底,然后再回头搜索。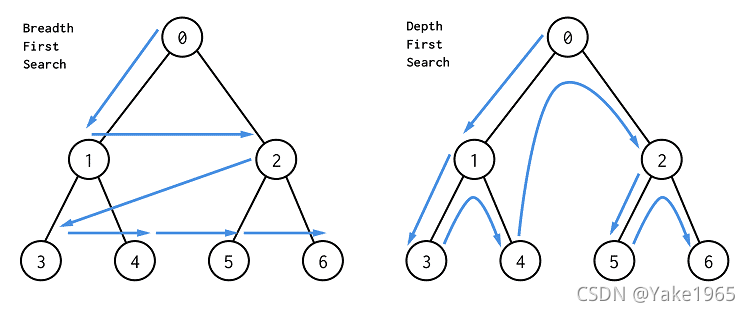
112. 路径总和
Leetcode
根结点到叶子结点的路径上值的和 :在叶子结点上判断。
方法一:递归 DFS
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if not root:return False
if not root.left and not root.right: # 叶子结点
return root.val == targetSum
# 问题转化为左右子树递归
return self.hasPathSum(root.right, targetSum - root.val) or self.hasPathSum(root.left, targetSum - root.val)
方法二:广度优先搜索 BFS
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if not root: return False
q = deque([(root, targetSum)]) # 通过元组携带值
while q:
cur, tem = q.popleft()
tem -= cur.val
if not cur.left and not cur.right: # 叶子结点
if tem == 0: return True
continue
cur.left and q.append((cur.left, tem))
cur.right and q.append((cur.right, tem))
return False
113. 路径总和 II
方法一:DFS
cclass Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
def dfs(cur, tem):
# 如果 path 作为参数传入,此处用 path = path + cur.val,就不用 copy 和回溯了。
path.append(cur.val)
tem -= cur.val
if not (cur.left or cur.right or tem):
res.append(path[:]) # copy
cur.left and dfs(cur.left, tem)
cur.right and dfs(cur.right, tem)
path.pop() # 回溯
if not root:return []
res , path = [], []
dfs(root, targetSum)
return res
方法二:BFS
class Solution:
def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
if not root: return []
res = []
q = deque([(root, [], targetSum)]) # 结点,路径,路径和
while q:
cur, path, tem = q.popleft()
# path += [cur.val]
# path.append(cur.val) # 列表 +=,append 对象不变 !!!
path = path + [cur.val] # 对象变了
tem -= cur.val
# 如果是叶子节点,同时和为零。
if not cur.left and not cur.right and not tem:
res.append(path) # 保存路径
cur.left and q.append((cur.left, path, tem))
cur.right and q.append((cur.right, path, tem))
return res
257. 二叉树的所有路径
DFS
一、空结点处理
1、递归中空结点返回
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
def dfs(node, path):
if not node: return # 空结点返回
path += str(node.val)
if not (node.left or node.right): # 叶子结点
res.append(path)
return
dfs(node.left, path + '->')
dfs(node.right, path + '->')
res = []
dfs(root, '')
return res
2、判断空结点,递归中不含空结点
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
def dfs(node, path):
path += str(node.val)
if not (node.left or node.right): # 叶子结点
res.append(path)
node.left and dfs(node.left, path + '->') # 判断空结点
node.right and dfs(node.right, path + '->')
res = []
dfs(root, '')
return res
二、路径全局变量与传参
全局变量需要拷贝与回溯,参数为不可变对象时不需要,参数各是各的,如上。参数是列表,使用 path = path + [root.val] 添加元素,事实上 path 已经变了。
1、path 定义成 list
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
def dfs(node):
path.append(node.val)
if not (node.left or node.right): # 叶子结点
res.append(path[:]) # copy
node.left and dfs(node.left)
node.right and dfs(node.right)
path.pop() # 回溯
path = []
res = []
dfs(root)
return ['->'.join(map(str,x)) for x in res]
2、path 定义成 str
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
def dfs(node):
nonlocal path
path += str(node.val) if node == root else '->' + str(node.val)
if not (node.left or node.right): # 叶子结点
res.append(path)
node.left and dfs(node.left)
node.right and dfs(node.right)
path = path.rsplit('->', 1)[0] # 回溯
path = ''
res = []
dfs(root)
return res
BFS
class Solution:
def binaryTreePaths(self, root: TreeNode) -> List[str]:
q = deque([(root, str(root.val))]) # 携带路径元组
res = []
while q:
cur, path = q.popleft()
if not cur.left and not cur.right: # 叶子结点
res.append(path)
cur.left and q.append((cur.left, path + '->' + str(cur.left.val)))
cur.right and q.append((cur.right, path + '->' + str(cur.right.val)))
return res
437. 路径总和 III
方法一:双重递归
class Solution:
def pathSum(self, root: TreeNode, targetSum: int) -> int:
def calPathSum(root, sum):
if not root: return 0
tmp = 0
sum -= root.val
if sum == 0:
tmp += 1
return tmp + calPathSum(root.left, sum) + calPathSum(root.right, sum)
if not root: return 0
return calPathSum(root, targetSum) + self.pathSum(root.left, targetSum) + self.pathSum(root.right, targetSum)
方法二:
class Solution:
def pathSum(self, root: TreeNode, targetSum: int) -> int:
def f(r, s):
if r:
s = [i + r.val for i in s] + [r.val]
return s.count(targetSum) + f(r.left, s) + f(r.right, s)
return 0
return f(root, [])
988. 从叶结点开始的最小字符串
方法一:DFS
class Solution:
def smallestFromLeaf(self, root: TreeNode) -> str:
def dfs(node, A):
if node:
A.append(node.val)
if not node.left and not node.right:
self.ans = min(self.ans, A[::-1])
dfs(node.left, A)
dfs(node.right, A)
A.pop()
self.ans = [27]
dfs(root, [])
return ''.join(map(lambda x:chr(x + ord('a')), self.ans))
方法二:BFS
class Solution:
def smallestFromLeaf(self, root: TreeNode) -> str:
res = []
q = deque([(root, [])])
while q:
cur, path = q.popleft()
path = [cur.val] + path
if not cur.left and not cur.right:
res.append(path)
cur.left and q.append((cur.left, path))
cur.right and q.append((cur.right, path))
ans = min(res)
return ''.join(map(lambda x:chr(x + 97), ans))
class Solution:
def smallestFromLeaf(self, root: TreeNode) -> str:
res = [27]
q = deque([(root, [])])
while q:
cur, path = q.popleft()
path = [cur.val] + path
if not cur.left and not cur.right:
res = min(res, path)
cur.left and q.append((cur.left, path))
cur.right and q.append((cur.right, path))
return ''.join(map(lambda x:chr(x + 97), res))
待整理…
124. 二叉树中的最大路径和
687. 最长同值路径
543. 二叉树的直径
vector<vector> res;
vector<vector> pathSum(TreeNode *root, int targetSum)
{
vector path;
dfs(root, targetSum, path);
return res;
}
void dfs(TreeNode*root, int sum, vector path)
{
if (!root)
return;
sum -= root->val;
path.push_back(root->val);
if (!root->left && !root->right && sum == 0)
{
res.push_back(path);
return;
}
dfs(root->left, sum, path);
dfs(root->right, sum, path);
}
437. 路径总和 III
双重递归:先调用dfs函数从root开始查找路径,再调用pathsum函数到root左右子树开始查找
没有通过
class Solution:
def __init__(self):
self.count = 0
def pathSum(self, root: TreeNode, sum: int) -> int:
@lru_cache(None)
def dfs(node, sum):
sum -= root.val
# 注意不要return,因为不要求到叶节点结束,所以一条路径下面还可能有另一条
if sum == 0:
self.count += 1 # 如果找到了一个路径全局变量就 + 1
node.left and dfs(node.left, sum)
node.right and dfs(node.right, sum)
if not root: return 0
dfs(root, sum)
self.pathSum(root.left, sum)
self.pathSum(root.right, sum)
return self.count
- 从叶结点开始的最小字符串
换汤不换药,套用模板1
vector path;
string smallestFromLeaf(TreeNode *root)
{
dfs(root, “”);
sort(path.begin(), path.end()); //升序排序
return path[0];
}
void dfs(TreeNode *root, string s)
{
if (!root)
return;
s += ‘a’ + root->val;
if (!root->left && !root->right)
{
reverse(s.begin(), s.end()); //题目要求从根节点到叶节点,因此反转
path.push_back(s);
return;
}
dfs(root->left, s);
dfs(root->right, s);
}
二、非自顶向下
124. 二叉树中的最大路径和
/left,right分别为根节点左右子树最大路径和,注意:如果最大路径和<0,意味着该路径和对总路径和做负贡献,因此不要计入到总路径中,将它设置为0
int res = INT_MIN; //注意节点值可能为负数,因此要设置为最小值
int maxPathSum(TreeNode *root)
{
maxPath(root);
return res;
}
int maxPath(TreeNode *root) //以root为路径起始点的最长路径
{
if (!root)
return 0;
int left = max(maxPath(root->left), 0);
int right = max(maxPath(root->right), 0);
res = max(res, left + right + root->val); //比较当前最大路径和与左右子树最长路径加上根节点值的较大值,更新全局变量
return max(left + root->val, right + root->val); //返回左右子树较长的路径加上根节点值
}
687. 最长同值路径
int longestUnivaluePath(TreeNode *root)
{
if (!root)
return 0;
longestPath(root);
return res;
}
int longestPath(TreeNode *root)
{
if (!root)
return 0;
int left = longestPath(root->left), right = longestPath(root->right);
// 如果存在左子节点和根节点同值,更新左最长路径;否则左最长路径为0
if (root->left && root->val == root->left->val)
left++;
else
left = 0;
if (root->right && root->val == root->right->val)
right++;
else
right = 0;
res = max(res, left + right);
return max(left, right);
}
543. 二叉树的直径
int res1 = 0;
int diameterOfBinaryTree(TreeNode *root)
{
maxPath(root);
return res1;
}
int maxPath(TreeNode *root)
{
// 这里递归结束条件要特别注意:不能是!root(而且不需要判断root为空,因为只有非空才会进入递归),因为单个节点路径长也是0
if (!root->left && !root->right)
return 0;
int left = root->left ? maxPath(root->left) + 1 : 0; //判断左子节点是否为空,从而更新左边最长路径
int right = root->right ? maxPath(root->right) + 1 : 0;
res1 = max(res, left + right); //更新全局变量
return max(left, right); //返回左右路径较大者
}
边栏推荐
- GEE(四):计算两个变量(影像)之间的相关性并绘制散点图
- Qt Graphicsview图形视图使用总结附流程图开发案例雏形
- Sword finger offer 27 Image of binary tree
- Comparison of various development methods of applets - cross end? Low code? Native? Or cloud development?
- Innovation today | five key elements for enterprises to promote innovation
- 每日一题——PAT乙级1002题
- Use JfreeChart to generate curves, histograms, pie charts, and distribution charts and display them to JSP-1
- There is another problem just online... Warm
- 行测-图形推理-2-黑白格类
- 微信论坛交流小程序系统毕业设计毕设(8)毕业设计论文模板
猜你喜欢
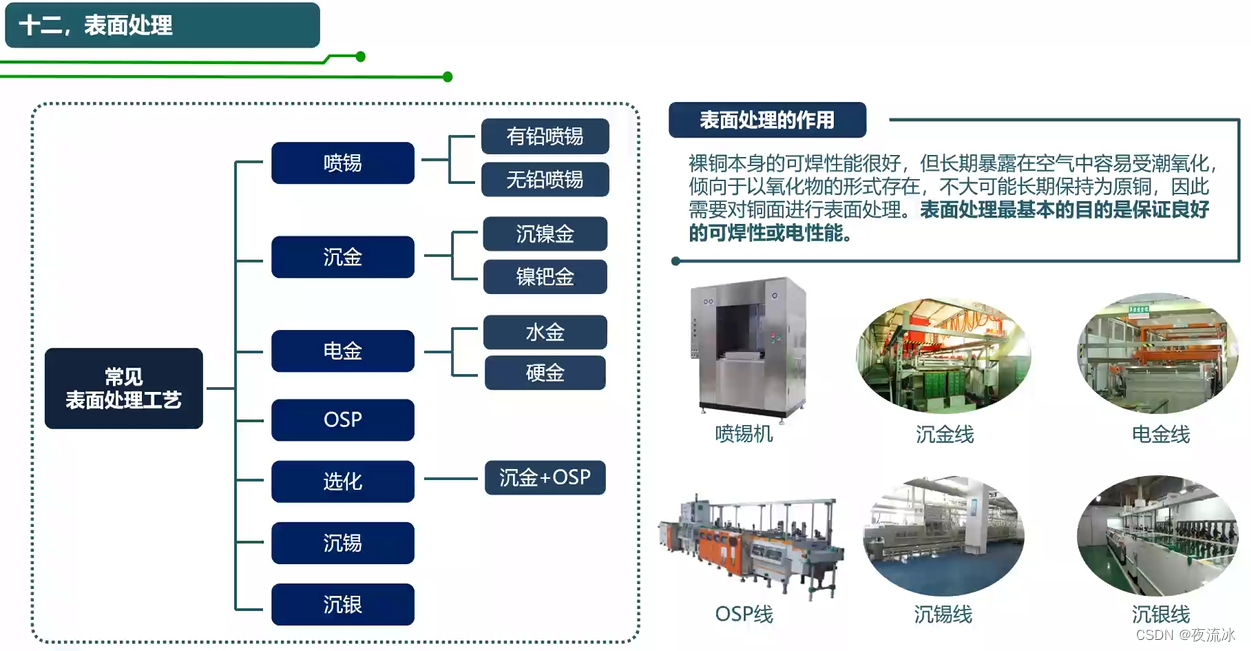
Knowledge drop - PCB manufacturing process flow

Cascade-LSTM: A Tree-Structured Neural Classifier for Detecting Misinformation Cascades-KDD2020
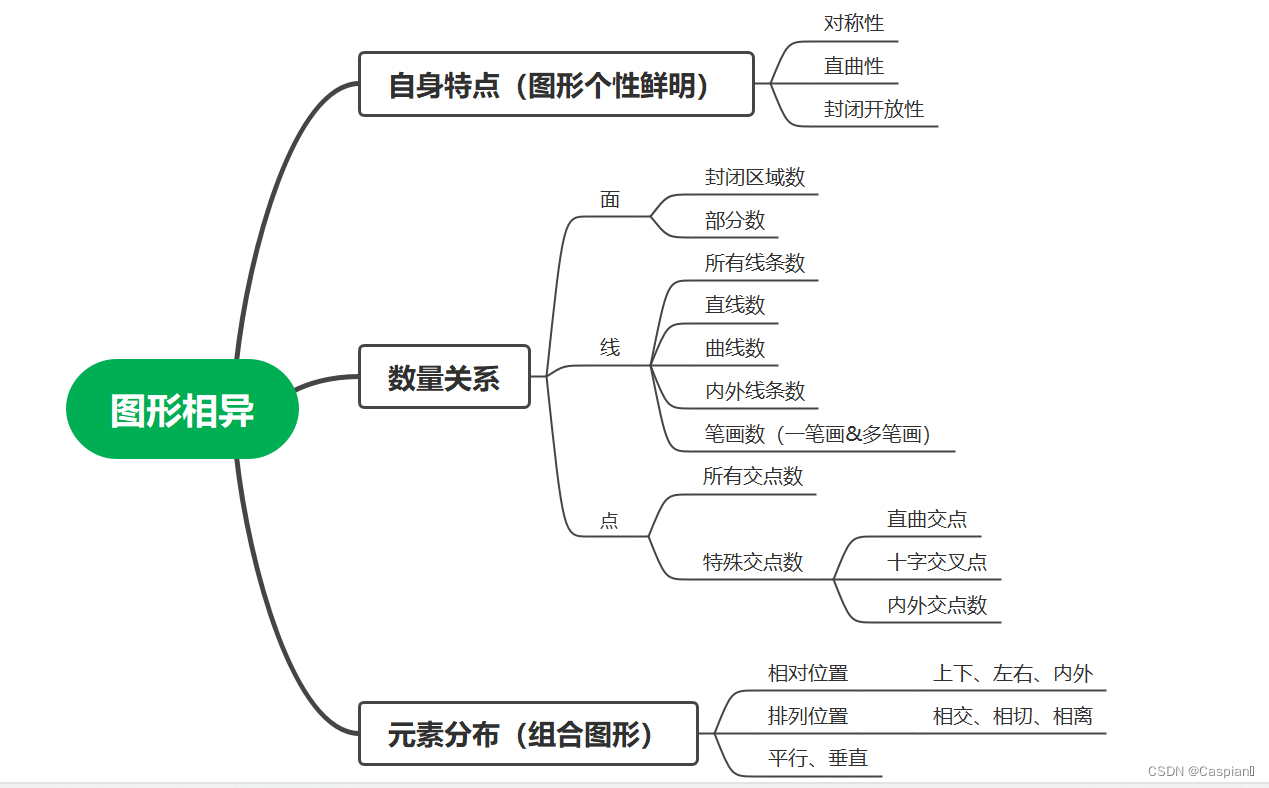
行测-图形推理-7-相异图形类

DTC社群运营怎么做?

Line test - graphic reasoning -7- different graphic classes

Force deduction - question 561 - array splitting I - step by step parsing
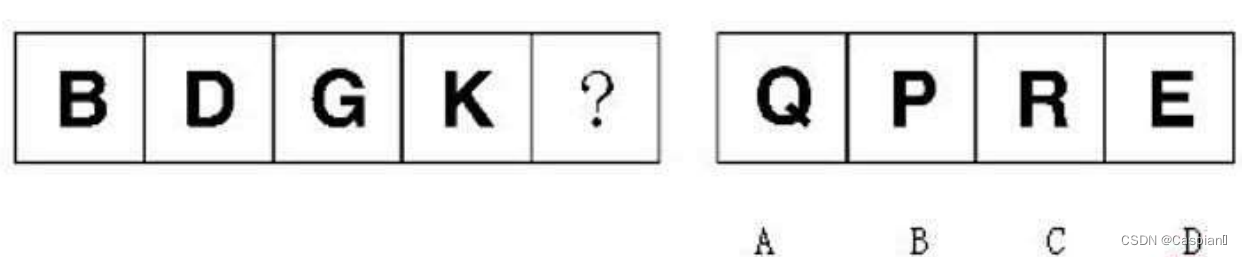
行测-图形推理-4-字母类
CTF exercise
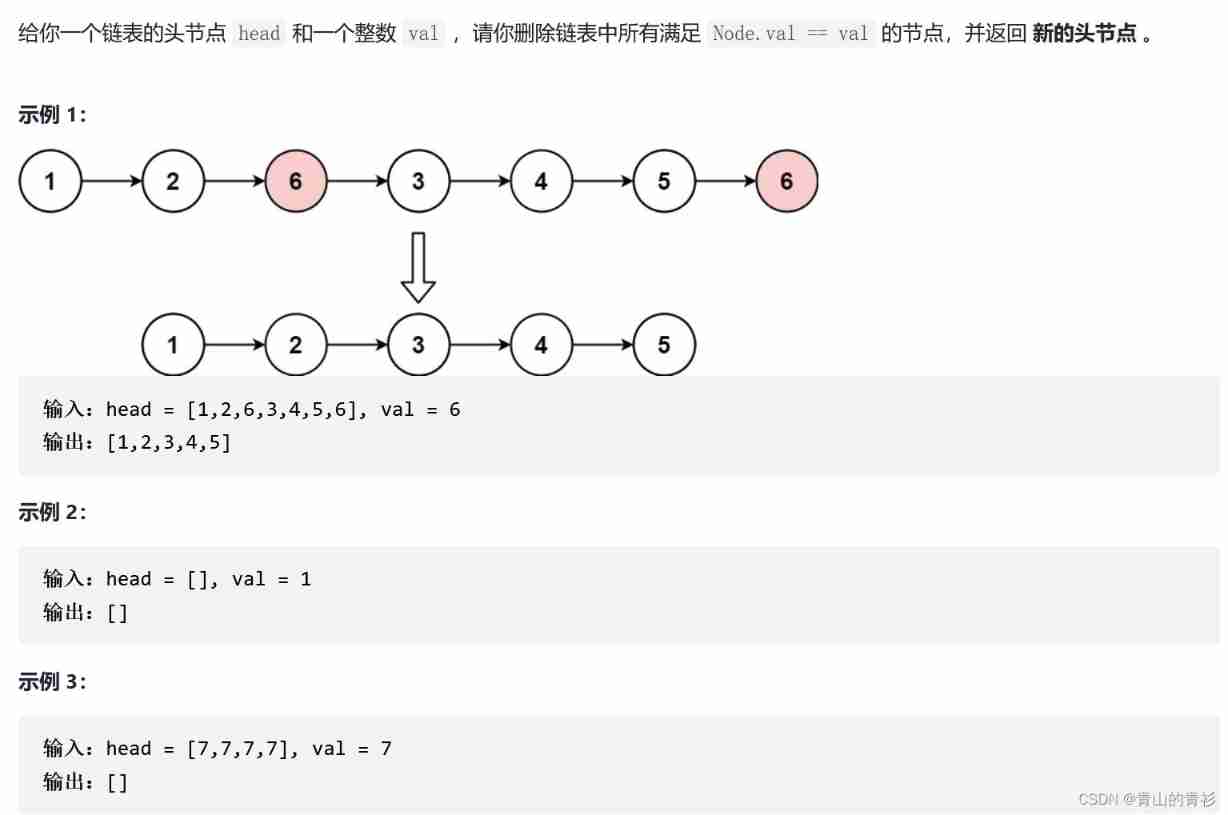
LeetCode203. Remove linked list elements
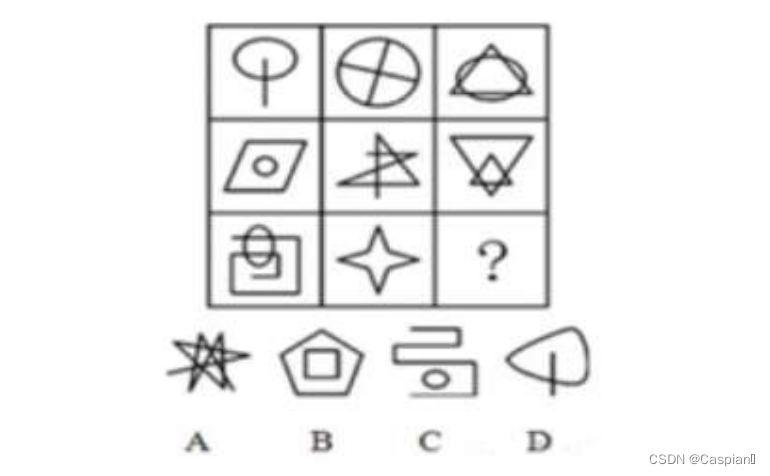
行测-图形推理-9-线条问题类
随机推荐
Transform XL translation
7-51 combination of two ordered linked list sequences
Ligne - raisonnement graphique - 4 - classe de lettres
Line test - graphic reasoning - 2 - black and white lattice class
Line measurement - graphic reasoning -9- line problem class
LeetCode144. Preorder traversal of binary tree
The wonderful relationship between message queue and express cabinet
双非大厂测试员亲述:对测试员来说,学历重要吗?
Lecture 30 linear algebra Lecture 5 eigenvalues and eigenvectors
Explain in detail the communication mode between arm A7 and risc-v e907 on Quanzhi v853
Leetcode19. Delete the penultimate node of the linked list [double pointer]
Talk about DART's null safety feature
GBU1510-ASEMI电源专用15A整流桥GBU1510
ArcGIS:字段赋值_属性表字段计算器(Field Calculator)依据条件为字段赋值
Cases of agile innovation and transformation of consumer goods enterprises
Sword finger offer 27 Image of binary tree
Microbial health network, how to restore microbial communities
行测-图形推理-2-黑白格类
2021-01-12
Mitsubishi PLC SLmP (MC) protocol