当前位置:网站首页>Summary of the mean value theorem of higher numbers
Summary of the mean value theorem of higher numbers
2022-07-07 05:21:00 【Full stack o-jay】
The mean value theorem
Generally used for proof questions , Analysis steps : Determine the interval 、 Determine auxiliary function 、 Determine the theorem used 、 Key point analysis .
f(x) stay [a,b] Continuous on ,
- Bounded and maximum theorem : m ≤ f ( x ) ≤ M m \leq f(x)\leq M m≤f(x)≤M
- Intermediate value theorem : m ≤ μ ≤ M , ∃ ϵ ∈ [ a , b ] , f ( ϵ ) = μ m\leq \mu \leq M, \exists \epsilon \in[a,b], f(\epsilon) = \mu m≤μ≤M,∃ϵ∈[a,b],f(ϵ)=μ
- Mean value theorem : a < x 1 < x 2 < ⋯ < x n < b , ∃ ϵ ∈ [ x 1 , x n ] , f ( ϵ ) = f ( x 1 ) + f ( x 2 ) + ⋯ + f ( x n ) n a<x_1<x_2<\cdots<x_n<b, \exists \epsilon \in[x_1,x_n], f(\epsilon) = \frac{f(x_1)+f(x_2)+\cdots+f(x_n)}{n} a<x1<x2<⋯<xn<b,∃ϵ∈[x1,xn],f(ϵ)=nf(x1)+f(x2)+⋯+f(xn)
- Zero point theorem : f ( a ) ⋅ f ( b ) < 0 , ∃ ϵ ∈ [ a , b ] , f ( ϵ ) = 0 f(a)\cdot f(b)<0, \exists \epsilon \in[a,b], f(\epsilon) = 0 f(a)⋅f(b)<0,∃ϵ∈[a,b],f(ϵ)=0
- Fermat's theorem : x 0 It's about can guide And by extremely value , f ′ ( x 0 ) = 0 x_0 Is differentiable and extremum , f'(x_0) = 0 x0 It's about can guide And by extremely value ,f′(x0)=0
- Rolle's theorem : [ a , b ) can guide , f ( a ) = f ( b ) , ∃ ϵ ∈ [ a , b ] , f ′ ( ϵ ) = 0 [a,b) Derivable , f(a) = f(b), \exists \epsilon \in[a,b], f'(\epsilon) = 0 [a,b) can guide ,f(a)=f(b),∃ϵ∈[a,b],f′(ϵ)=0
- Lagrange mean value theorem : ( a , b ) can guide , ∃ ϵ ∈ [ a , b ] , f ( b ) − f ( a ) = f ′ ( ϵ ) ( b − a ) (a,b) Derivable , \exists \epsilon \in[a,b], f(b) - f(a) = f'(\epsilon)(b-a) (a,b) can guide ,∃ϵ∈[a,b],f(b)−f(a)=f′(ϵ)(b−a)
- Cauchy mean value theorem : ( a , b ) can guide , g ′ ( x ) ≠ 0 , ∃ ϵ ∈ [ a , b ] , f ( b ) − f ( a ) g ( b ) − g ( a ) = f ′ ( ϵ ) g ′ ( ϵ ) (a,b) Derivable , g'(x)\neq 0, \exists \epsilon \in[a,b], \frac{f(b) - f(a)}{g(b) - g(a)} = \frac{f'(\epsilon)}{g'(\epsilon)} (a,b) can guide ,g′(x)=0,∃ϵ∈[a,b],g(b)−g(a)f(b)−f(a)=g′(ϵ)f′(ϵ)
- Taylor formula ( lagrange remainder ): f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + ⋯ + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + f ( n + 1 ) ( ϵ ) ( n + 1 ) ! ( x − x 0 ) n + 1 f(x) = f(x_0) + f'(x_0)(x-x_0)+\cdots+ \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n +\frac{f^{(n+1)}(\epsilon)}{(n+1)!}(x-x_0)^{n+1} f(x)=f(x0)+f′(x0)(x−x0)+⋯+n!f(n)(x0)(x−x0)n+(n+1)!f(n+1)(ϵ)(x−x0)n+1
- Taylor formula ( Payano's remainder ): f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + ⋯ + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + O ( ( x − x 0 ) n ) f(x) = f(x_0) + f'(x_0)(x-x_0)+\cdots+ \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n +O((x-x_0)^n) f(x)=f(x0)+f′(x0)(x−x0)+⋯+n!f(n)(x0)(x−x0)n+O((x−x0)n)
- Mean value theorem of integral : ∃ ϵ ∈ [ a , b ] , ∫ a b f ( x ) d x b − a = f ( ϵ ) \exists \epsilon \in[a,b], \frac{\int_a^bf(x)dx}{b-a} = f(\epsilon) ∃ϵ∈[a,b],b−a∫abf(x)dx=f(ϵ)
There is a memory skill , The most commonly used are seven ,“ Zero dielectric ferroratesi ”, If you see the proof question, you can try it one by one ,
边栏推荐
- Longest common subsequence (LCS) (dynamic programming, recursive)
- Timer创建定时器
- U++4 interface learning notes
- Leetcode(417)——太平洋大西洋水流问题
- c语言神经网络基本代码大全及其含义
- Safe landing practice of software supply chain under salesforce containerized ISV scenario
- Wonderful express | Tencent cloud database June issue
- SQL injection - secondary injection and multi statement injection
- Array initialization of local variables
- 《5》 Table
猜你喜欢

数字化如何影响工作流程自动化
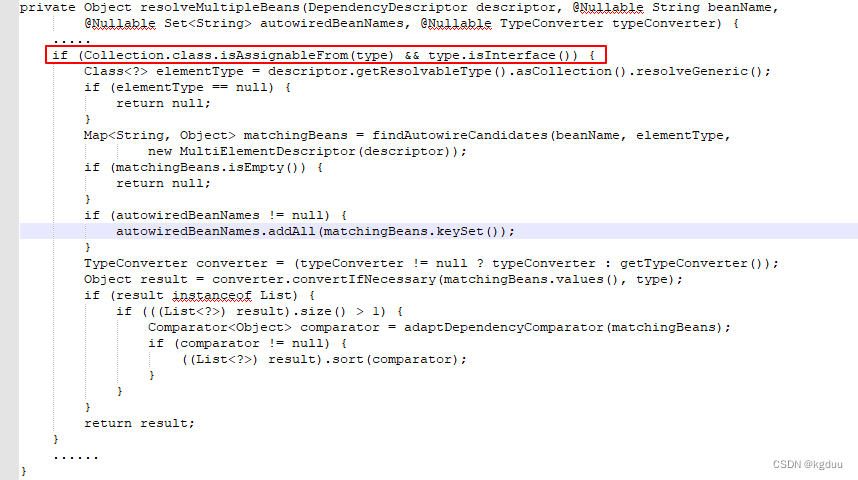
Phenomenon analysis when Autowired annotation is used for list
![[opencv] image morphological operation opencv marks the positions of different connected domains](/img/c3/f437bad9432dedbbb14c8a62ba5180.png)
[opencv] image morphological operation opencv marks the positions of different connected domains

JHOK-ZBL1漏电继电器
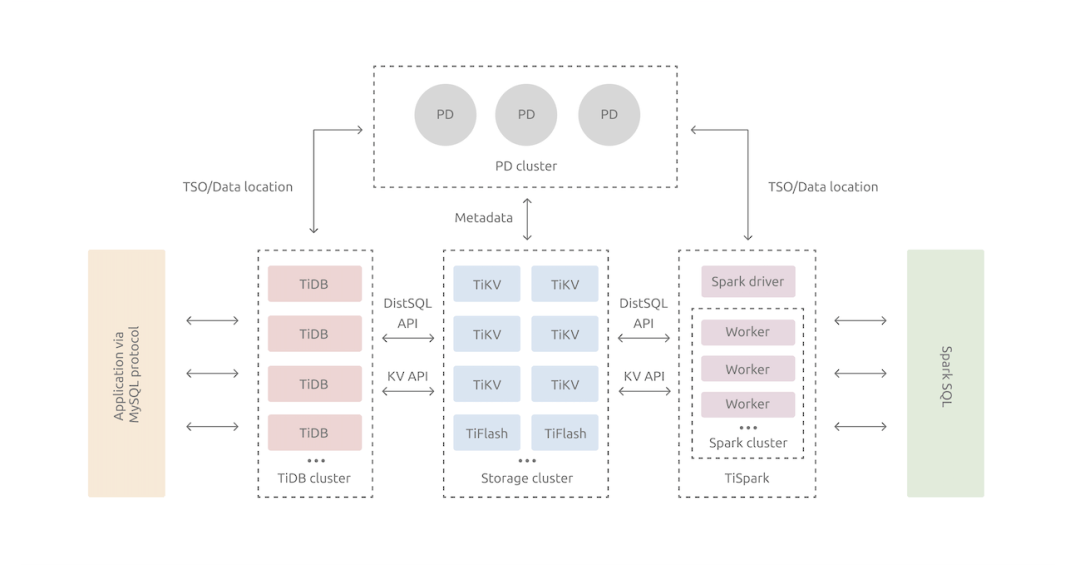
10 distributed databases that take you to the galaxy
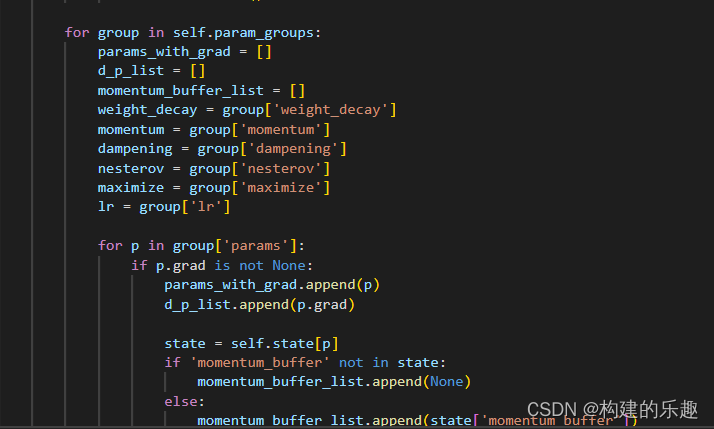
torch optimizer小解析
sublime使用技巧

【js组件】date日期显示。

Dynamically generate tables
SQL injection - secondary injection and multi statement injection
随机推荐
3. Type of fund
JVM(十九) -- 字节码与类的加载(四) -- 再谈类的加载器
最长公共子序列(LCS)(动态规划,递归)
Two methods of thread synchronization
DJ-ZBS2漏电继电器
2. Overview of securities investment funds
照片选择器CollectionView
利用OPNET进行网络任意源组播(ASM)仿真的设计、配置及注意点
Vector and class copy constructors
Linkedblockingqueue source code analysis - initialization
Longest non descent subsequence (LIS) (dynamic programming)
How can project managers counter attack with NPDP certificates? Look here
磁盘监控相关命令
线程池的创建与使用
Batch normalization (Standardization) processing
最全常用高数公式
A cool "ghost" console tool
ASP. Net MVC - resource cannot be found error - asp Net MVC – Resource Cannot be found error
Dynamically generate tables
Simulate thread communication