当前位置:网站首页>最全常用高数公式
最全常用高数公式
2022-07-06 22:42:00 【全栈O-Jay】
文章目录
1 等价无穷小 ( x → 0 x\to 0 x→0)
s i n x ∼ x sinx\sim x sinx∼x, t a n x ∼ x tanx\sim x tanx∼x, a r c s i n x ∼ x arcsinx\sim x arcsinx∼x, a r c t a n x ∼ x arctanx\sim x arctanx∼x, e x − 1 ∼ x e^x -1\sim x ex−1∼x, I n ( 1 + x ) ∼ x In(1+x)\sim x In(1+x)∼x,
a x − 1 = e x I n a − 1 ∼ x I n a a^x-1= e^{xIna}-1\sim xIna ax−1=exIna−1∼xIna, 1 − c o s x ∼ 1 2 x 2 1-cosx\sim \frac{1}{2}x^2 1−cosx∼21x2, ( 1 + x ) a − 1 ∼ a x (1+x)^a -1\sim ax (1+x)a−1∼ax,
小 + 大 ∼ 大 小+大\sim 大 小+大∼大, ∫ 0 x f ( t ) d t ∼ x \int_{0}^{x}f(t)dt\sim x ∫0xf(t)dt∼x
2 常用公式
2.1 和式夹逼准则的两个思路
n → ∞ : n ⋅ u m i n ≤ ∑ i = 1 n u i ≤ n ⋅ u m a x n → 有 限 : 1 ⋅ u m a x ≤ ∑ i = 1 n u i ≤ n ⋅ u m a x n\to \infty : n\cdot u_{min}\leq \sum\limits_{i=1}^{n}u_i \leq n\cdot u_{max}\\ n\to 有限 : 1\cdot u_{max}\leq \sum\limits_{i=1}^{n}u_i \leq n\cdot u_{max} n→∞:n⋅umin≤i=1∑nui≤n⋅umaxn→有限:1⋅umax≤i=1∑nui≤n⋅umax
2.2 小基础
- ( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + b 3 (a+b)^3 = a^3+ 3a^2b + 3ab^2 + b^3 (a+b)3=a3+3a2b+3ab2+b3
- a 3 − b 3 = ( a − b ) ( a 2 + a b + b 3 ) a^3-b^3 = (a-b)(a^2 + ab + b^3) a3−b3=(a−b)(a2+ab+b3)
- ( a + b ) n = ∑ k = 0 n C n k a n − k b k (a+b)^n = \sum\limits_{k=0}^{n}C_n^ka^{n-k}b^k (a+b)n=k=0∑nCnkan−kbk
- ∑ k = 1 n k 2 = n ( n + 1 ) ( 2 n + 1 ) 6 \sum\limits_{k=1}^{n}k^2 = \frac{n(n+1)(2n+1)}{6} k=1∑nk2=6n(n+1)(2n+1)
- ∑ n = 1 ∞ 1 n 2 = π 2 6 \sum\limits_{n=1}^{\infty}\frac{1}{n^2} = \frac{\pi ^2}{6} n=1∑∞n21=6π2
2.3 一元二次方程解
X 1 , 2 = − b ± b 2 − 4 a c 2 a , X 1 + X 2 = − b a , X 1 X 2 = a c , 顶 点 : ( − b 2 a , c − b 2 4 a ) X_{1,2} = \frac{-b\pm \sqrt{b^2-4ac}}{2a}, X_1 + X_2 = -\frac{b}{a}, X_1X_2 = \frac{a}{c},\\顶点: (-\frac{b}{2a} , c-\frac{b^2}{4a}) X1,2=2a−b±b2−4ac,X1+X2=−ab,X1X2=ca,顶点:(−2ab,c−4ab2)
3 * \bigstar *常用展开公式 * \bigstar *
- e x = 1 + x + x 2 2 ! + ⋯ = ∑ n = 0 ∞ x n n ! e^x = 1+x+\frac{x^2}{2!}+\cdots =\sum\limits_{n=0}^{\infty}\frac{x^n}{n!} ex=1+x+2!x2+⋯=n=0∑∞n!xn
- I n ( 1 + x ) = x − x 2 2 + ⋯ = ∑ n = 0 ∞ ( − 1 ) n − 1 x n n ( − 1 < x ≤ 1 ) In(1+x) = x-\frac{x^2}{2}+\cdots =\sum\limits_{n=0}^{\infty}(-1)^{n-1}\frac{x^n}{n}\quad (-1<x\leq 1) In(1+x)=x−2x2+⋯=n=0∑∞(−1)n−1nxn(−1<x≤1)
- I n ( 1 − x ) = − ∑ n = 0 ∞ x n n ( − 1 < x ≤ 1 ) In(1-x) = -\sum\limits_{n=0}^{\infty}\frac{x^n}{n}\quad (-1<x\leq 1) In(1−x)=−n=0∑∞nxn(−1<x≤1)
- 1 1 − x = 1 + x + x 2 + ⋯ = ∑ n = 0 ∞ x n ∣ x ∣ < 1 \frac{1}{1-x} = 1+x+x^2+\cdots =\sum\limits_{n=0}^{\infty}x^n\quad \mid x\mid <1 1−x1=1+x+x2+⋯=n=0∑∞xn∣x∣<1
- s i n x = x − x 3 3 ! + ⋯ = ∑ n = 0 − ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! sinx = x-\frac{x^3}{3!}+\cdots =\sum\limits_{n=0}^{-\infty}(-1)^{n}\frac{x^{2n+1}}{(2n+1)!} sinx=x−3!x3+⋯=n=0∑−∞(−1)n(2n+1)!x2n+1
- c o s x = 1 − x 2 2 ! + ⋯ = ∑ n = 0 − ∞ ( − 1 ) n x 2 n ( 2 n ) ! cosx = 1-\frac{x^2}{2!}+\cdots =\sum\limits_{n=0}^{-\infty}(-1)^{n}\frac{x^{2n}}{(2n)!} cosx=1−2!x2+⋯=n=0∑−∞(−1)n(2n)!x2n
- t a n x = x + x 3 3 + O ( x 3 ) tanx = x+\frac{x^3}{3}+O(x^3) tanx=x+3x3+O(x3)
- a r c s i n x = x + x 3 6 + O ( x 3 ) arcsinx = x+\frac{x^3}{6}+O(x^3) arcsinx=x+6x3+O(x3)
- a r c t a n x = x − x 3 3 + O ( x 3 ) = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 2 n + 1 arctanx = x-\frac{x^3}{3}+O(x^3) = \sum\limits_{n=0}^{\infty}(-1)^{n}\frac{x^{2n+1}}{2n+1} arctanx=x−3x3+O(x3)=n=0∑∞(−1)n2n+1x2n+1
- e x − e − x 2 = ∑ n = 0 ∞ x 2 n + 1 ( 2 n + 1 ) ! \frac{e^x-e^{-x}}{2} = \sum\limits_{n=0}^{\infty}\frac{x^{2n+1}}{(2n+1)!} 2ex−e−x=n=0∑∞(2n+1)!x2n+1
- e x + e − x 2 = ∑ n = 0 ∞ x 2 n ( 2 n ) ! \frac{e^x+e^{-x}}{2} = \sum\limits_{n=0}^{\infty}\frac{x^{2n}}{(2n)!} 2ex+e−x=n=0∑∞(2n)!x2n
- ( 1 + x ) a = 1 + a x + a ( a − 1 ) 2 x 2 + O ( x 2 ) (1+x)^a = 1+ax+\frac{a(a-1)}2{x^2} + O(x^2) (1+x)a=1+ax+2a(a−1)x2+O(x2)
4 常用不等式
- a r c t a n x < x < a r c s i n x ( 0 ≤ x ≤ 1 ) arctanx < x < arcsinx \quad (0\leq x\leq 1) arctanx<x<arcsinx(0≤x≤1)
- e x ≥ x + 1 ( ∀ x ) e^x \geq x+1\quad (∀x) ex≥x+1(∀x)
- x − 1 ≥ I n x ( x > 0 ) x-1 \geq Inx\quad (x>0) x−1≥Inx(x>0)
- x > s i n x ( x > 0 ) x> sinx\quad (x>0) x>sinx(x>0)
- 1 1 + x < I n ( 1 + 1 x ) < 1 x \frac{1}{1+x}<In(1+\frac{1}{x})<\frac{1}{x} 1+x1<In(1+x1)<x1
- x 1 + x < I n ( 1 + x ) < x \frac{x}{1+x}<In(1+x)<x 1+xx<In(1+x)<x
- a b ≤ a + b 2 ≤ a 2 + b 2 2 ( a , b > 0 ) \sqrt{ab}\leq \frac{a+b}{2}\leq \sqrt{\frac{a^2+b^2}{2}}\quad (a,b>0) ab≤2a+b≤2a2+b2(a,b>0)
- a b c 3 ≤ a + b + c 3 ( a , b , c > 0 ) \sqrt[3]{abc}\leq \frac{a+b+c}{3}\quad (a,b,c>0) 3abc≤3a+b+c(a,b,c>0)
- ∣ a ± b ∣ ≤ ∣ a ∣ + ∣ b ∣ \mid a\pm b\mid \leq \mid a\mid + \mid b\mid ∣a±b∣≤∣a∣+∣b∣
- ∣ ∣ a ∣ − ∣ b ∣ ∣ ≤ ∣ a − b ∣ \mid \mid a\mid - \mid b\mid \mid \leq \mid a-b\mid ∣∣a∣−∣b∣∣≤∣a−b∣
- ∣ ∫ a b f ( x ) d x ∣ ≤ ∫ a b ∣ f ( x ) ∣ d x \mid \int_a^bf(x)dx\mid \leq \int_a^b\mid f(x)\mid dx ∣∫abf(x)dx∣≤∫ab∣f(x)∣dx
5 三角变换
- 诱导公式法则:奇变偶不变,符号看象限!
- s i n 2 x = 2 s i n x c o s x sin2x = 2sinxcosx sin2x=2sinxcosx
- c o s 2 x = c o s 2 x − s i n 2 x = 1 − 2 s i n 2 x = 2 c o s 2 − 1 cos2x = cos^2x - sin^2x = 1-2sin^2x = 2cos^2-1 cos2x=cos2x−sin2x=1−2sin2x=2cos2−1
- s i n 3 x = − 4 s i n 3 x + 3 s i n x sin3x = -4sin^3x + 3sinx sin3x=−4sin3x+3sinx
- c o s 3 x = 4 c o s 2 x − 3 c o s x cos3x = 4cos^2x - 3cosx cos3x=4cos2x−3cosx
- s i n x ⋅ c o s y = 1 2 [ s i n ( x + y ) + s i n ( x − y ) ] sinx\cdot cosy = \frac{1}{2}[sin(x+y)+sin(x-y)] sinx⋅cosy=21[sin(x+y)+sin(x−y)]
- s i n 2 x 2 = 1 2 ( 1 − c o s x ) sin^2\frac{x}{2} = \frac{1}{2}(1-cosx) sin22x=21(1−cosx)
- c o s 2 x 2 = 1 2 ( 1 + c o s x ) cos^2\frac{x}{2} = \frac{1}{2}(1+cosx) cos22x=21(1+cosx)
- t a n 2 x 2 = 1 − c o s x s i n x = s i n x 1 + c o s x tan^2\frac{x}{2} = \frac{1-cosx}{sinx} = \frac{sinx}{1+cosx} tan22x=sinx1−cosx=1+cosxsinx
- s i n x = 2 t a n x 2 1 + t a n 2 x 2 sinx = \frac{2tan\frac{x}{2}}{1+tan^2\frac{x}{2}} sinx=1+tan22x2tan2x
- c o s x = 1 − t a n 2 x 2 1 + t a n 2 x 2 cosx = \frac{1-tan^2\frac{x}{2}}{1+tan^2\frac{x}{2}} cosx=1+tan22x1−tan22x
- t a n 2 x = 2 t a n x 1 − t a n 2 x tan2x = \frac{2tanx}{1-tan^2x} tan2x=1−tan2x2tanx
- c o t 2 x = c o t 2 x − 1 2 c o t x cot2x = \frac{cot^2x - 1}{2cotx} cot2x=2cotxcot2x−1
- 1 + t a n 2 x = s e c 2 x 1+tan^2x = sec^2x 1+tan2x=sec2x
- 1 + c o t 2 x = c s c 2 x 1+cot^2x = csc^2x 1+cot2x=csc2x
6 * \bigstar *微分 * \bigstar *
6.1 定义式
- f ′ ( x 0 ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 f'(x_0) = \lim\limits_{\Delta x\to{0}}\frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = \lim\limits_{x\to{x_0}}\frac{f(x) - f(x_0)}{x-x_0} f′(x0)=Δx→0limΔxf(x0+Δx)−f(x0)=x→x0limx−x0f(x)−f(x0)
- f ( n ) ( x 0 ) = lim x → x 0 f ( n − 1 ) ( x ) − f ( n − 1 ) ( x 0 ) x − x 0 f^{(n)}(x_0) = \lim\limits_{x\to{x_0}} \frac{f^{(n-1)}(x) - f^{(n-1)}(x_0)}{x-x_0} f(n)(x0)=x→x0limx−x0f(n−1)(x)−f(n−1)(x0)
- 连续 ⇏ \nRightarrow ⇏ 可导,可导 ⇒ \Rightarrow ⇒ 连续,可导 ⇔ \Leftrightarrow ⇔ 可微
6.2 常用难记微分公式
- ( t a n x ) ′ = s e c 2 x (tanx)' = sec^2x (tanx)′=sec2x
- ( c o t x ) ′ = − c s c 2 x (cotx)' = -csc^2x (cotx)′=−csc2x
- ( s e c x ) ′ = s e c x t a n x , ( c s c x ) ′ = − c s c x c o t x (secx)' = secxtanx, (cscx)' = -cscxcotx (secx)′=secxtanx,(cscx)′=−cscxcotx
- ( a r c s i n x ) ′ = 1 1 − x 2 , ( a r c c o s x ) ′ = − 1 1 − x 2 (arcsinx)' = \frac{1}{\sqrt{1-x^2}},\quad (arccosx)' = -\frac{1}{\sqrt{1-x^2}} (arcsinx)′=1−x21,(arccosx)′=−1−x21
- ( a r c t a n x ) ′ = 1 1 + x 2 , ( a r c c o t x ) ′ = − 1 1 + x 2 (arctanx)' = \frac{1}{1+x^2},\quad (arccotx)' = -\frac{1}{1+x^2} (arctanx)′=1+x21,(arccotx)′=−1+x21
- ( I n ∣ c o s x ∣ ) ′ = − t a n x (In\mid cosx\mid)' = -tanx (In∣cosx∣)′=−tanx
- ( I n ∣ s i n x ∣ ) ′ = c o t x (In\mid sinx\mid)' = cotx (In∣sinx∣)′=cotx
- ( I n ∣ s e c x + t a n x ∣ ) ′ = s e c x (In\mid secx + tanx\mid)' = secx (In∣secx+tanx∣)′=secx
- ( I n ∣ c s c x − c o t x ∣ ) ′ = c s c x (In\mid cscx - cotx\mid)' = cscx (In∣cscx−cotx∣)′=cscx
- [ I n ( x + x 2 ± a 2 ) ] ′ = 1 x 2 ± a 2 [In(x+\sqrt{x^2\pm a^2})]' = \frac{1}{\sqrt{x^2\pm a^2}} [In(x+x2±a2)]′=x2±a21
- d x 2 = ( d x ) 2 dx^2 = (dx)^2 dx2=(dx)2
- d ( x 2 ) = 2 x d x d(x^2) = 2xdx d(x2)=2xdx
- ( u v w ) ′ = u ′ v w + u v ′ w + u v w ′ (uvw)' = u'vw+uv'w+uvw' (uvw)′=u′vw+uv′w+uvw′
- ( u v ) ( n ) = ∑ k = 0 n C n k u ( n − k ) v ( k ) (uv)^{(n)} = \sum\limits_{k=0}^{n}C_n^ku^{(n-k)}v^{(k)} (uv)(n)=k=0∑nCnku(n−k)v(k)
6.3 分析函数关注点
定义域、奇偶性、对称性、图形变换、单调性、极值、最值、凹凸性、拐点、三种渐近线(铅垂、水平、斜)
7 * \bigstar *积分 * \bigstar *
7.1 定积分定义
- ∫ a b f ( x ) d x = lim n → ∞ ∑ i = 1 ∞ f ( a + b − a n i ) b − a n \int_a^bf(x)dx =\lim\limits_{n\to{\infty}} \sum\limits_{i=1}^{\infty} f(a+\frac{b-a}{n}i)\frac{b-a}{n} ∫abf(x)dx=n→∞limi=1∑∞f(a+nb−ai)nb−a
- ∫ 0 1 f ( x ) d x = lim n → ∞ ∑ i = 1 ∞ f ( i n ) 1 n \int_0^1f(x)dx =\lim\limits_{n\to{\infty}} \sum\limits_{i=1}^{\infty} f(\frac{i}{n})\frac{1}{n} ∫01f(x)dx=n→∞limi=1∑∞f(ni)n1
- ∫ 0 x f ( x ) d x = lim n → ∞ ∑ i = 1 ∞ f ( x n i ) x n \int_0^xf(x)dx =\lim\limits_{n\to{\infty}} \sum\limits_{i=1}^{\infty} f(\frac{x}{n}i)\frac{x}{n} ∫0xf(x)dx=n→∞limi=1∑∞f(nxi)nx
7.2 基本积分表
- ∫ x k d x = 1 k + 1 x k + 1 + C \int x^k dx = \frac{1}{k+1}x^{k+1} + C ∫xkdx=k+11xk+1+C
- ∫ a x d x = a x I n a + C \int a^x dx = \frac{a^x}{Ina} +C ∫axdx=Inaax+C
- ∫ s i n x d x = − c o s + C \int sinx dx = -cos +C ∫sinxdx=−cos+C
- ∫ c o s d x = s i n x + C \int cos dx = sinx +C ∫cosdx=sinx+C
- ∫ t a n x d x = − I n ∣ c o s x ∣ + C \int tanx dx = -In\mid cosx\mid +C ∫tanxdx=−In∣cosx∣+C
- ∫ c o t x d x = I n ∣ s i n x ∣ + C \int cotx dx = In\mid sinx\mid +C ∫cotxdx=In∣sinx∣+C
- ∫ s e c x d x = I n ∣ s e c x + t a n x ∣ + C \int secx dx = In\mid secx + tanx\mid +C ∫secxdx=In∣secx+tanx∣+C
- ∫ c s c x d x = I n ∣ c s c x − c o t x ∣ + C \int cscx dx = In\mid cscx - cotx\mid +C ∫cscxdx=In∣cscx−cotx∣+C
- ∫ s e c 2 x d x = t a n x + C \int sec^2x dx = tanx +C ∫sec2xdx=tanx+C
- ∫ c s c 2 x d x = − c o t x + C \int csc^2x dx = -cotx +C ∫csc2xdx=−cotx+C
- ∫ s e c x t a n x d x = s e c x + C \int secxtanx dx = secx +C ∫secxtanxdx=secx+C
- ∫ c s c x c o t x d x = − c s c x + C \int cscxcotx dx = -cscx +C ∫cscxcotxdx=−cscx+C
- ∫ 1 1 − x 2 d x = a r c s i n x + C \int \frac{1}{\sqrt{1-x^2}} dx = arcsinx +C ∫1−x21dx=arcsinx+C
- ∫ 1 a 2 − x 2 d x = a r c s i n x a + C \int \frac{1}{\sqrt{a^2-x^2}} dx = arcsin\frac{x}{a} +C ∫a2−x21dx=arcsinax+C
- ∫ 1 1 + x 2 d x = a r c t a n x + C \int \frac{1}{1+x^2} dx = arctanx +C ∫1+x21dx=arctanx+C
- ∫ 1 a 2 + x 2 d x = 1 a a r c t a n x a + C ( a > 0 ) \int \frac{1}{a^2+x^2} dx = \frac{1}{a}arctan\frac{x}{a} +C\quad (a>0) ∫a2+x21dx=a1arctanax+C(a>0)
- ∫ 1 x 2 + a 2 d x = I n ( x + x 2 + a 2 ) + C \int \frac{1}{\sqrt{x^2+a^2}} dx = In(x+\sqrt{x^2+a^2}) +C ∫x2+a21dx=In(x+x2+a2)+C
- ∫ 1 x 2 − a 2 d x = I n ( x + x 2 − a 2 ) + C ( ∣ x ∣ > ∣ a ∣ ) \int \frac{1}{\sqrt{x^2-a^2}} dx = In(x+\sqrt{x^2-a^2}) +C\quad (\mid x\mid>\mid a\mid) ∫x2−a21dx=In(x+x2−a2)+C(∣x∣>∣a∣)
- ∫ 1 x 2 − a 2 d x = 1 2 a I n ∣ x − a x + a ∣ + C \int \frac{1}{x^2-a^2} dx = \frac{1}{2a}In\mid \frac{x-a}{x+a}\mid +C ∫x2−a21dx=2a1In∣x+ax−a∣+C
- ∫ 1 a 2 − x 2 d x = 1 2 a I n ∣ x + a x − a ∣ + C \int \frac{1}{a^2-x^2} dx = \frac{1}{2a}In\mid \frac{x+a}{x-a}\mid +C ∫a2−x21dx=2a1In∣x−ax+a∣+C
- ∫ a 2 − x 2 d x = a 2 2 a r c s i n x a + x 2 a 2 − x 2 + C ( ∣ x ∣ < a ) \int \sqrt{a^2-x^2} dx = \frac{a^2}{2}arcsin\frac{x}{a} + \frac{x}{2}\sqrt{a^2-x^2} +C\quad (\mid x\mid<a) ∫a2−x2dx=2a2arcsinax+2xa2−x2+C(∣x∣<a)
- ∫ s i n 2 x d x = x 2 − s i n 2 x 4 + C \int sin^2x dx = \frac{x}{2} -\frac{sin2x}{4} +C ∫sin2xdx=2x−4sin2x+C
- ∫ c o s 2 x d x = x 2 + s i n 2 x 4 + C \int cos^2x dx = \frac{x}{2} +\frac{sin2x}{4} +C ∫cos2xdx=2x+4sin2x+C
7.3 常用积分公式
- ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x \int_a^b f(x) dx = \int_a^b f(a+b-x) dx ∫abf(x)dx=∫abf(a+b−x)dx
- ∫ a b f ( x ) d x = 1 2 ∫ a b [ f ( x ) + f ( a + b − x ) ] d x \int_a^b f(x) dx = \frac{1}{2} \int_a^b [f(x)+f(a+b-x)] dx ∫abf(x)dx=21∫ab[f(x)+f(a+b−x)]dx
- ∫ a b f ( x ) d x = ∫ a a + b 2 [ f ( x ) + f ( a + b − x ) ] d x \int_a^b f(x) dx = \int_a^{\frac{a+b}{2}} [f(x)+f(a+b-x)] dx ∫abf(x)dx=∫a2a+b[f(x)+f(a+b−x)]dx
- 点火公式: ∫ 0 π 2 s i n n x d x = ∫ 0 π 2 c o s n x d x = n − 1 n n − 3 n − 2 ⋯ \int_0^\frac{\pi}{2}sin^nxdx = \int_0^\frac{\pi}{2}cos^nxdx = \frac{n-1}{n} \frac{n-3}{n-2} \cdots ∫02πsinnxdx=∫02πcosnxdx=nn−1n−2n−3⋯
- ∫ 0 π x f ( s i n x ) d x = π 2 ∫ 0 π f ( s i n x ) d x = π ∫ 0 π 2 f ( s i n x ) \int_0^{\pi} xf(sinx) dx = \frac{\pi}{2}\int_0^{\pi} f(sinx) dx =\pi \int_0^{\frac{\pi}{2}} f(sinx) ∫0πxf(sinx)dx=2π∫0πf(sinx)dx=π∫02πf(sinx)
- ∫ 0 π 2 f ( s i n x ) d x = ∫ 0 π 2 f ( c o s x ) d x \int_0^{\frac{\pi}{2}} f(sinx) dx = \int_0^{\frac{\pi}{2}} f(cosx) dx ∫02πf(sinx)dx=∫02πf(cosx)dx
- ∫ 0 π 2 f ( s i n x , c o s x ) d x = ∫ 0 π 2 f ( c o s x , s i n x ) d x \int_0^{\frac{\pi}{2}} f(sinx, cosx) dx = \int_0^{\frac{\pi}{2}} f(cosx,sinx) dx ∫02πf(sinx,cosx)dx=∫02πf(cosx,sinx)dx
- ∫ a b f ( x ) d x = ∫ − π 2 π 2 f ( a + b 2 + b − a 2 s i n t ) ⋅ b − a 2 c o s t d t , ( x − a + b 2 = b − a 2 s i n t ) \int_a^b f(x) dx = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} f(\frac{a+b}{2} + \frac{b-a}{2} sint)\cdot \frac{b-a}{2}cost dt, \quad (x-\frac{a+b}{2} = \frac{b-a}{2}sint) ∫abf(x)dx=∫−2π2πf(2a+b+2b−asint)⋅2b−acostdt,(x−2a+b=2b−asint)
- ∫ a b f ( x ) d x = ∫ 0 1 ( b − a ) f [ a + ( b − a ) t ] d t , ( x − a = ( b − a ) t ) \int_a^b f(x) dx = \int_{0}^{1} (b-a) f[a+(b-a)t] dt, \quad (x-a = (b-a)t) ∫abf(x)dx=∫01(b−a)f[a+(b−a)t]dt,(x−a=(b−a)t)
- ∫ − a a f ( x ) d x = ∫ 0 a [ f ( x ) + f ( − x ) ] d x \int_{-a}^a f(x) dx = \int_{0}^{a} [f(x) + f(-x)] dx ∫−aaf(x)dx=∫0a[f(x)+f(−x)]dx
- ∫ 0 n π x ∣ s i n x ∣ d x = n 2 π \int_0^{n\pi} x\mid sinx\mid dx = n^2\pi ∫0nπx∣sinx∣dx=n2π
7.4 积分常用方法
凑微分、换元、分部积分、通分
全部手打,如果觉得有帮助帮忙点个赞啦蟹蟹!之后会继续补全高数下的公式,可以先收藏哦。
边栏推荐
- Gpt-3 is a peer review online when it has been submitted for its own research
- 【736. Lisp 语法解析】
- National meteorological data / rainfall distribution data / solar radiation data /npp net primary productivity data / vegetation coverage data
- npm ERR! 400 Bad Request - PUT xxx - “devDependencies“ dep “xx“ is not a valid dependency name
- Jetson nano configures pytorch deep learning environment / / to be improved
- In depth analysis of kubebuilder
- Ansible overview and module explanation (you just passed today, but yesterday came to your face)
- STM32F103ZE+SHT30检测环境温度与湿度(IIC模拟时序)
- The most complete learning rate adjustment strategy in history LR_ scheduler
- Oracle - views and sequences
猜你喜欢
Function pointer and pointer function in C language

为什么很多人对技术债务产生误解
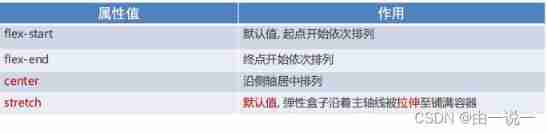
Flex layout and usage

A line of R code draws the population pyramid
指针与数组在函数中输入实现逆序输出
![[line segment tree practice] recent requests + area and retrieval - array modifiable + my schedule I / III](/img/13/d598bb53b71fbadd4a97c603152124.png)
[line segment tree practice] recent requests + area and retrieval - array modifiable + my schedule I / III
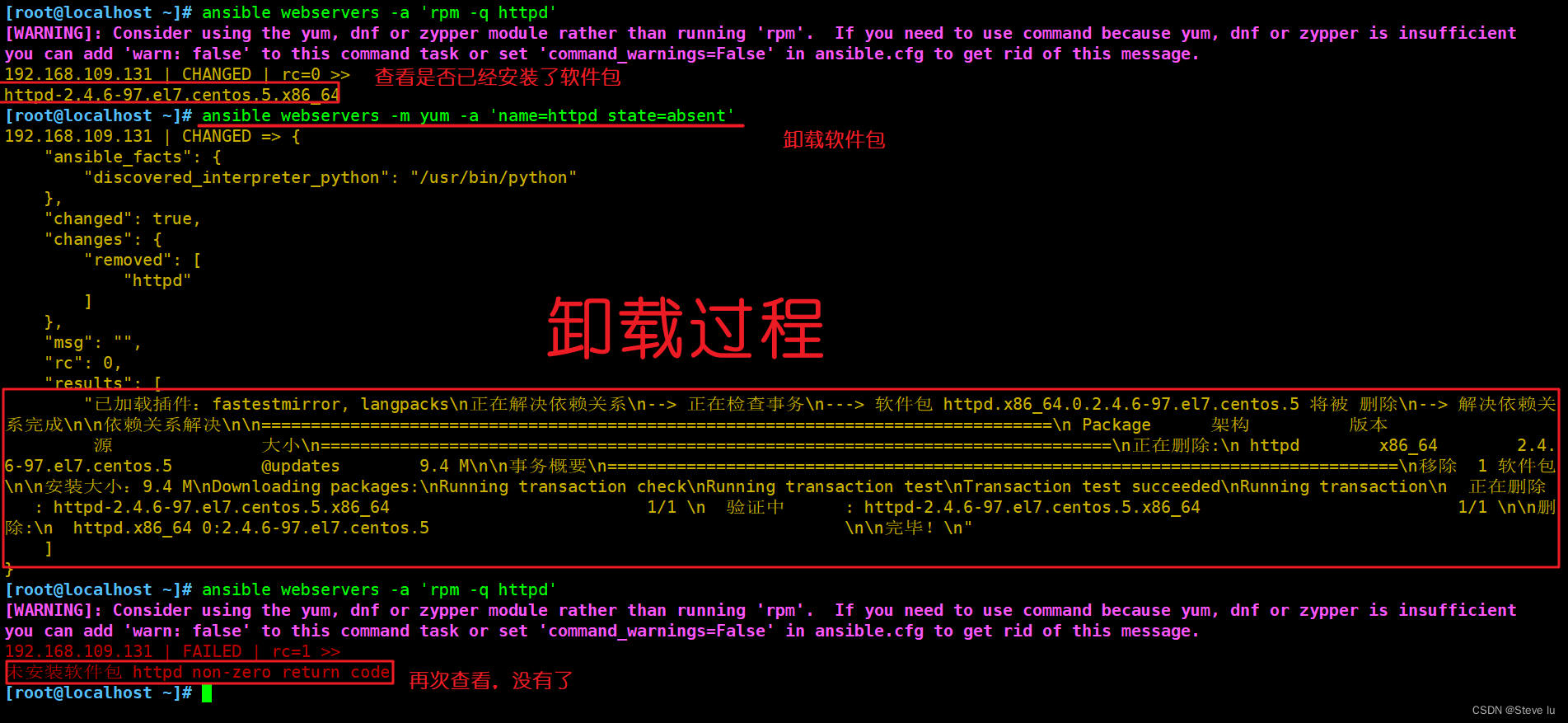
Ansible overview and module explanation (you just passed today, but yesterday came to your face)

Ansible报错:“msg“: “Invalid/incorrect password: Permission denied, please try again.“

U++ 元数据说明符 学习笔记
namespace基础介绍
随机推荐
Depth first traversal template principle of tree and graph
namespace基础介绍
【ArcGIS教程】专题图制作-人口密度分布图——人口密度分析
[line segment tree practice] recent requests + area and retrieval - array modifiable + my schedule I / III
leetcode 53. Maximum subarray maximum subarray sum (medium)
Time complexity & space complexity
组织实战攻防演练的5个阶段
Mysql database (basic)
A detailed explanation of head pose estimation [collect good articles]
Liste des hôtes d'inventaire dans ansible (je vous souhaite des fleurs et de la romance sans fin)
Gavin teacher's perception of transformer live class - rasa project actual combat e-commerce retail customer service intelligent business dialogue robot microservice code analysis and dialogue experim
Can I specify a path in an attribute to map a property in my class to a child property in my JSON?
Servicemesh mainly solves three pain points
MySQL数据库(基础篇)
Meaning of 'n:m' and '1:n' in database design
Stm32f103ze+sht30 detection of ambient temperature and humidity (IIC simulation sequence)
深入解析Kubebuilder
JS variable case
史上最全学习率调整策略lr_scheduler
架构实战训练营|课后作业|模块 6