当前位置:网站首页>acwing 843. N-queen problem
acwing 843. N-queen problem
2022-07-07 04:38:00 【_ Liu Xiaoyu】
n− The Queen's problem means that n Put a queen in n×n On my chess board , So that the queen can't attack each other , That is, no two Queens can be in the same line 、 On the same column or slash .
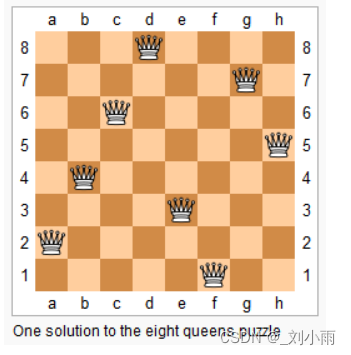
Now, given an integer n, Please output all the pieces that meet the conditions .
Input format
All in one line , Contains integers n.
Output format
Each solution accounts for n That's ok , Each line outputs a length of n String , Used to represent the complete chessboard state .
among . Indicates that the grid status of a position is empty ,Q The queen is placed on the square indicating a certain position .
After the output of each scheme is completed , Output a blank line .
Be careful : There must be no extra spaces at the end of the line .
The order of output schemes is arbitrary , As long as there is no repetition and no omission .
Data range
1≤n≤9
sample input :
4
sample output :
.Q…
…Q
Q…
…Q.
…Q.
Q…
…Q
.Q…
This question is also DFS, It can be arranged according to
solution 1: Enumerate by row ( It's also the same question Full Permutation Allied )
It can be remembered as a template

#include <iostream>
using namespace std;
const int N = 20;
// bool Array is used to determine whether the next location of the search is feasible
// col Column ,dg Diagonals ,udg Anti diagonal
// g[N][N] Used to save path
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
void dfs(int u) {
// u == n It means that we have searched n That's ok , So output this path
if (u == n) {
for (int i = 0; i < n; i ++ ) puts(g[i]); // Equivalent to cout << g[i] << endl;
puts(""); // Line break
return;
}
// enumeration u This business , Search for legal Columns , // Here, we can regard line as y, Column as x
// Here is the enumeration number u That's ok , The first i Column , Whether to release the queen , u= y, i = x after ===》 The diagonal is u + i、u - i + n
for (int i = 0; i < n; i ++ )
// prune ( For points that do not meet the requirements , No more searching )
if (!col[i] && !dg[u + i] && !udg[n - i + u])
{
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - i + u] = true;
dfs(u + 1);
col[i] = dg[u + i] = udg[n - i + u] = false;
g[u][i] = '.'; // Restore the scene
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0);
return 0;
}
Method 2: Enumerate according to each element
Every position has 2 In this case , Put it or not , There is... In all n2
Time complexity : O(2 Of n2 Power ), I can't fight it out , Forgive me
Schematic diagram : Draw like this 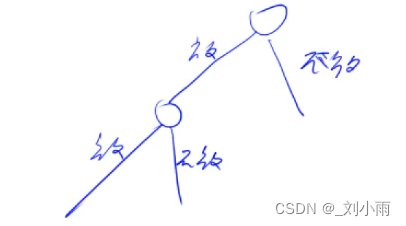
Ideas : Search step by step according to each position .
code:
// Different search order Time complexity is different So the search order is very important !
#include <iostream>
using namespace std;
const int N = 20;
int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N]; // Because it's a search , So I added row
// s Indicates the number of queens that have been put on
void dfs(int x, int y, int s)
{
// Deal with situations beyond the boundary , Whether to put this directly in one line or not , After walking , Jump to the next line to start
if (y == n) y = 0, x ++ ;
if (x == n) {
// x==n Description has been enumerated n^2 It's a place
if (s == n) {
// s==n It means that it was successfully put on n A queen
for (int i = 0; i < n; i ++ ) puts(g[i]);
puts("");
}
return;
}
// Branch 1: Put the queen
if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]) {
g[x][y] = 'Q';
row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
dfs(x, y + 1, s + 1);
row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
g[x][y] = '.';
}
// Branch 2: Don't let the queen go
dfs(x, y + 1, s);
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0, 0, 0);
return 0;
}
边栏推荐
- 機器人(自動化)課程的持續學習-2022-
- A detailed explanation of head pose estimation [collect good articles]
- VM virtual machine operating system not found and NTLDR is missing
- Lecture 3 of "prime mover x cloud native positive sounding, cost reduction and efficiency enhancement lecture" - kubernetes cluster utilization improvement practice
- 程序员上班摸鱼,这么玩才高端!
- 各路行业大佬称赞的跨架构开发“神器”,你get同款了吗?
- Why does WordPress open so slowly?
- leetcode 53. Maximum Subarray 最大子数组和(中等)
- [coded font series] opendyslexic font
- Ssm+jsp realizes enterprise management system (OA management system source code + database + document +ppt)
猜你喜欢
Mathematical analysis_ Notes_ Chapter 10: integral with parameters

MySQL forgot how to change the password
![[coded font series] opendyslexic font](/img/5e/e1512ffe494b5d0e7d6d6765644126.png)
[coded font series] opendyslexic font
Optimization of channel status offline of other server devices caused by easycvr cluster restart

EasyCVR无法使用WebRTC进行播放,该如何解决?
How to open win11 remote desktop connection? Five methods of win11 Remote Desktop Connection
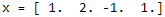
mpf2_线性规划_CAPM_sharpe_Arbitrage Pricin_Inversion Gauss Jordan_Statsmodel_Pulp_pLU_Cholesky_QR_Jacobi
这项15年前的「超前」技术设计,让CPU在AI推理中大放光彩
Win11控制面板快捷键 Win11打开控制面板的多种方法

【实践出真理】import和require的引入方式真的和网上说的一样吗
随机推荐
EasyCVR视频广场点击播放时,主菜单高亮效果消失问题的修复
kivy教程之设置窗体大小和背景(教程含源码)
[ArcGIS tutorial] thematic map production - population density distribution map - population density analysis
Digital chemical plant management system based on Virtual Simulation Technology
深耕开发者生态,加速AI产业创新发展 英特尔携众多合作伙伴共聚
[team learning] [34 sessions] Alibaba cloud Tianchi online programming training camp
Golang compresses and decompresses zip files
测试/开发程序员怎么升职?从无到有,从薄变厚.......
Golang calculates constellations and signs based on birthdays
Detect when a tab bar item is pressed
过气光刻机也不能卖给中国!美国无理施压荷兰ASML,国产芯片再遭打压
Zero knowledge private application platform aleo (1) what is aleo
Win11截图键无法使用怎么办?Win11截图键无法使用的解决方法
Kivy tutorial of setting the size and background of the form (tutorial includes source code)
[system management] clear the icon cache of deleted programs in the taskbar
Ssm+jsp realizes the warehouse management system, and the interface is called an elegant interface
MySQL split method usage
Win11图片打不开怎么办?Win11无法打开图片的修复方法
MySQL forgot how to change the password
Break the memory wall with CPU scheme? Learn from PayPal to expand the capacity of aoteng, and the volume of missed fraud transactions can be reduced to 1/30