当前位置:网站首页>DFS and BFS concepts and practices +acwing 842 arranged numbers (DFS) +acwing 844 Maze walking (BFS)
DFS and BFS concepts and practices +acwing 842 arranged numbers (DFS) +acwing 844 Maze walking (BFS)
2022-07-07 04:38:00 【_ Liu Xiaoyu】
DFS ( Deep search ), It is also said to be recursive
persistent : Keep searching to the end , Then go back to the next node
data structure : stack, Space :O(h) h: It's height
It does not have the shortest circuit property ( The idea is strange , Those with high space requirements )
Important concepts : to flash back , prune
BFS ( Wide search )
Calm and steady : Layer by layer search
data structure : queue, Space :O(2h) h: It's height
It has the shortest circuit property ( When the weight of each path is 1)
DFS Example explanation : Can be used to understand recursive Thought
acwing 842 Arrange numbers
Given an integer n, The digital 1∼n In a row , There will be many ways to arrange .
Now? , Please output all the arrangement methods in dictionary order .
Input format
All in one line , Contains an integer n.
Output format
Output all permutation schemes in dictionary order , One line for each scheme .
Data range
1≤n≤7
sample input :
3
sample output :
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
thought :
For the full permutation problem , You can draw the following search tree 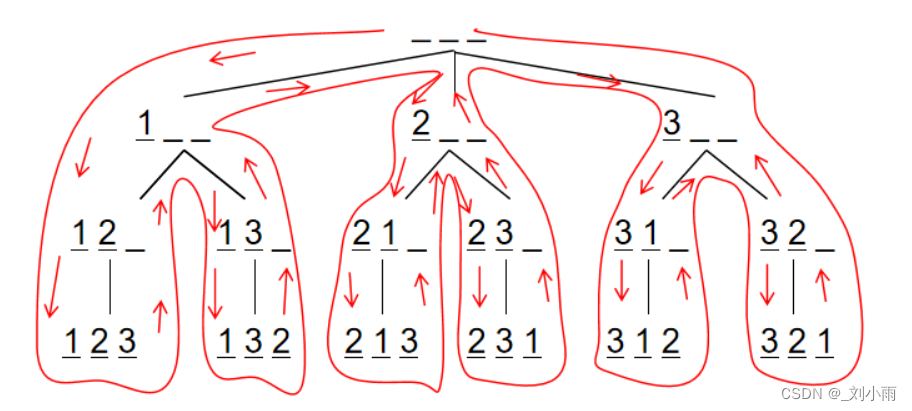
The whole process of recursive function call 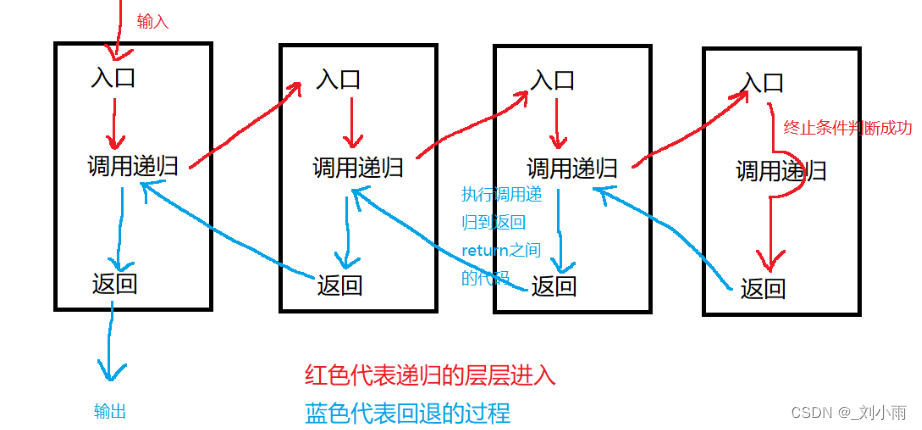
code:
// Backtracking is the stack callback automatically allocated in the system .
#include <iostream>
using namespace std;
const int N = 10;
int n;
int path[N];
bool st[N]; // Whether to traverse the points before saving == true It means that it has passed
void dfs(int u)
{
if(u == n)
{
// Explain that all positions are filled , From here 0 Start , stay main Function , Corresponding from 0 Start
for(int i=0; i<n; i++) cout << path[i] << ' ';
cout << endl;
return;
}
// Here is to determine which points can be selected
for(int i=1; i<=n; i++) // Here we need to find out which points have not been enumerated
{
if(!st[i])
{
path[u] = i;
st[i] = true;
dfs(u+ 1);
// Restore the scene
st[i] = false;
//path[u] = 0; // You can delete , Because the value here is overwritten
}
}
}
int main()
{
cin >> n;
dfs(0); // From 0 Start looking at
return 0;
}
Explain the above code flow :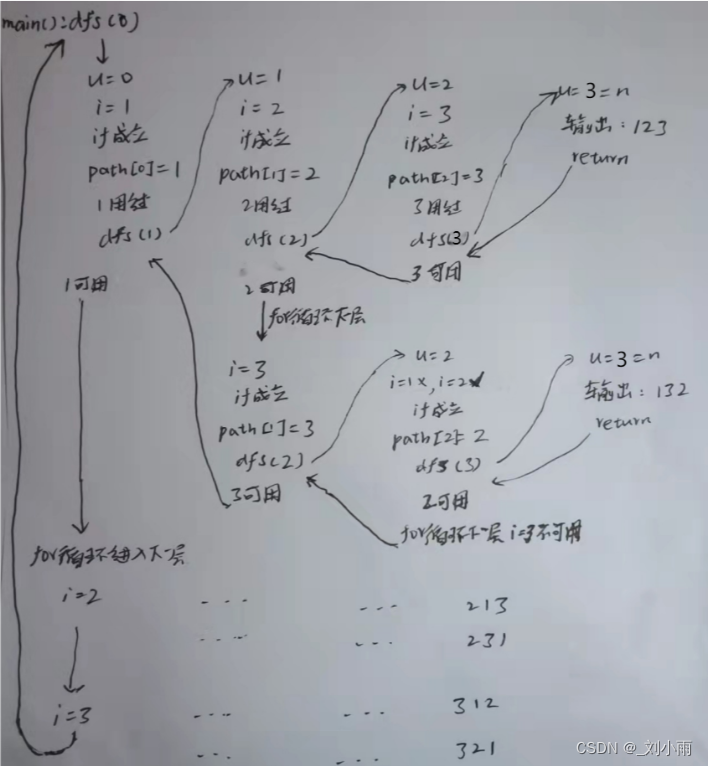
BFS: Why can we find the shortest circuit
It is searched layer by layer , Only when the weights in the graph are the same , This search is the shortest way
DFS Generally, there is no commonly used framework , however BFS Wide search There are commonly used frameworks , So look down
Common solution steps :
- The initial state is put into the queue
- Put in while, Not empty
- stay while in Every time I get to the head of the team
- Expand Team head
- end
Pseudo code :
queue <- The initial state
while queue Not empty
{
t <- Team head
Expand t
}
Examples : acwing 844. Labyrinth
Given a n×m A two-dimensional array of integers , Used to represent a maze , The array contains only 0 or 1, among 0 Means the way to go ,1 Indicates an impassable wall .
first , There is a man in the upper left corner (1,1) It's about , It is known that the person can go up every time 、 Next 、 Left 、 Move a position in any right direction .
Excuse me, , The person moves from the upper left corner to the lower right corner (n,m) It's about , At least how many times you need to move .
Data assurance (1,1) Place and (n,m) The number at is 0, And there must be at least one path .
Input format
The first line contains two integers n and m.
Next n That's ok , Each row contains m It's an integer (0 or 1), Represents a complete two-dimensional array .
Output format
Output an integer , Represents the minimum number of moves from the upper left corner to the lower right corner .
Data range
1≤n,m≤100
sample input :
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
sample output :
8
Ideas :
- use g[][] Store maps , use d[][] Store starting point to n,m Distance of
- From the starting point, breadth first traverse the map
- When the map is traversed , The distance from the starting point to each point is calculated , Output d[n][m] that will do

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int g[N][N]; // Store maps
int d[N][N]; // Storage distance
int n, m;
int bfs()
{
queue<PII> q;
q.push({
0, 0});
memset(d, -1, sizeof d);
d[0][0] = 0;
while(!q.empty())
{
PII start = q.front();
q.pop();
g[start.first][start.second] = 1; // I've been through
int dx[4] = {
-1, 0, 1, 0}, dy[4] = {
0, 1, 0 ,-1};
for(int i =0; i < 4; i++)
{
int x = start.first + dx[i], y = start.second + dy[i];
if(!g[x][y] && x >= 0 && x < n && y >= 0 && y < m && d[x][y] == -1) // It means you haven't walked , Description optional
{
g[x][y] = 1;
d[x][y] = d[start.first][start.second] + 1;
//cout << d[x][y] << endl;
q.push({
x, y});
}
}
}
// d The shortest distance of the path that can be walked has been saved in the array ( To {0,0})
return d[n - 1][m - 1];
}
int main()
{
cin >> n >> m;
memset(g, 1, sizeof g); // You can't go without initialization
for(int i = 0; i < n; i ++)
for(int j =0; j < m; j ++)
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
The following is the path code if you want to output
Ideas : Output backward from the last position
Method : use Pre[][] Save the location information of the previous point
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int g[N][N]; // Store maps
int d[N][N]; // Storage distance
int n, m;
PII Pre[N][N]; // Save the points passed
int bfs()
{
queue<PII> q;
q.push({
0, 0});
memset(d, -1, sizeof d);
d[0][0] = 0;
while(!q.empty())
{
PII start = q.front();
q.pop();
g[start.first][start.second] = 1; // I've been through
int dx[4] = {
-1, 0, 1, 0}, dy[4] = {
0, 1, 0 ,-1};
for(int i =0; i < 4; i++)
{
int x = start.first + dx[i], y = start.second + dy[i];
if(!g[x][y] && x >= 0 && x < n && y >= 0 && y < m && d[x][y] == -1) // It means you haven't walked , Description optional
{
g[x][y] = 1;
Pre[x][y] = start;
d[x][y] = d[start.first][start.second] + 1;
//cout << d[x][y] << endl;
q.push({
x, y});
}
}
}
// The following is the output of the path from the end
int x = n - 1, y = m - 1;
while(x || y)
{
cout << x << ' ' << y << endl;
auto t = Pre[x][y];
x = t.first, y= t.second;
}
// d The shortest distance of the path that can be walked has been saved in the array ( To {0,0})
return d[n - 1][m - 1];
}
int main()
{
cin >> n >> m;
memset(g, 1, sizeof g); // You can't go without initialization
for(int i = 0; i < n; i ++)
for(int j =0; j < m; j ++)
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
The operation results are as follows :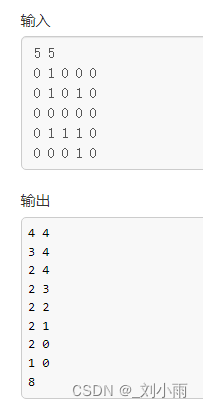
边栏推荐
- Deeply cultivate the developer ecosystem, accelerate the innovation and development of AI industry, and Intel brings many partners together
- Poor math students who once dropped out of school won the fields award this year
- [team learning] [34 issues] scratch (Level 2)
- Win11远程桌面连接怎么打开?Win11远程桌面连接的五种方法
- A picture to understand! Why did the school teach you coding but still not
- Zhou Yajin, a top safety scholar of Zhejiang University, is a curiosity driven activist
- 组织实战攻防演练的5个阶段
- Zero knowledge private application platform aleo (1) what is aleo
- SSM+jsp实现仓库管理系统,界面那叫一个优雅
- Win11图片打不开怎么办?Win11无法打开图片的修复方法
猜你喜欢
System framework of PureMVC
Video fusion cloud platform easycvr video Plaza left column list style optimization
namespace基础介绍

NFT meta universe chain diversified ecosystem development case

DFS和BFS概念及实践+acwing 842 排列数字(dfs) +acwing 844. 走迷宫(bfs)

【线段树实战】最近的请求次数 + 区域和检索 - 数组可修改+我的日程安排表Ⅰ/Ⅲ
Ssm+jsp realizes enterprise management system (OA management system source code + database + document +ppt)

See Gardenia minor
Win11图片打不开怎么办?Win11无法打开图片的修复方法
機器人(自動化)課程的持續學習-2022-
随机推荐
[team learning] [phase 34] Baidu PaddlePaddle AI talent Creation Camp
英特尔与信步科技共同打造机器视觉开发套件,协力推动工业智能化转型
Digital chemical plants realize the coexistence of advantages of high quality, low cost and fast efficiency
过气光刻机也不能卖给中国!美国无理施压荷兰ASML,国产芯片再遭打压
Win11控制面板快捷键 Win11打开控制面板的多种方法
Introduction to the PureMVC series
Lecture 3 of "prime mover x cloud native positive sounding, cost reduction and efficiency enhancement lecture" - kubernetes cluster utilization improvement practice
Different meat customers joined hands with Dexter to launch different hamburgers in some stores across the country
Optimization of channel status offline of other server devices caused by easycvr cluster restart
leetcode 53. Maximum Subarray 最大子数组和(中等)
Ssm+jsp realizes the warehouse management system, and the interface is called an elegant interface
案例大赏:英特尔携众多合作伙伴推动多领域AI产业创新发展
Hardware development notes (10): basic process of hardware development, making a USB to RS232 module (9): create ch340g/max232 package library sop-16 and associate principle primitive devices
AI表现越差,获得奖金越高?纽约大学博士拿出百万重金,悬赏让大模型表现差劲的任务
MySQL split method usage
Digital chemical plant management system based on Virtual Simulation Technology
Unity3d can change colors and display samples in a building GL material
B站大佬用我的世界搞出卷积神经网络,LeCun转发!爆肝6个月,播放破百万
On the 110th anniversary of Turing's birth, has the prediction of intelligent machine come true?
论文上岸攻略 | 如何快速入门学术论文写作