当前位置:网站首页>acwing 843. n-皇后问题
acwing 843. n-皇后问题
2022-07-06 22:04:00 【_刘小雨】
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
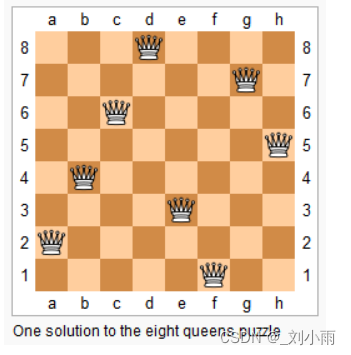
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
4
输出样例:
.Q…
…Q
Q…
…Q.
…Q.
Q…
…Q
.Q…
这题也是DFS, 可以根据全排列的
解法1:按行枚举 (也是跟上一题 全排列类似的)
可以作为模版进行记忆

#include <iostream>
using namespace std;
const int N = 20;
// bool数组用来判断搜索的下一个位置是否可行
// col列,dg对角线,udg反对角线
// g[N][N]用来存路径
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
void dfs(int u) {
// u == n 表示已经搜了n行,故输出这条路径
if (u == n) {
for (int i = 0; i < n; i ++ ) puts(g[i]); // 等价于cout << g[i] << endl;
puts(""); // 换行
return;
}
// 枚举u这一行,搜索合法的列, // 这里可将行看成y, 列看成x
// 这里是枚举第u行, 第i 列, 是否放皇后, u= y, i = x 后 ===》 对角线就是 u + i、u - i + n
for (int i = 0; i < n; i ++ )
// 剪枝(对于不满足要求的点,不再继续往下搜索)
if (!col[i] && !dg[u + i] && !udg[n - i + u])
{
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - i + u] = true;
dfs(u + 1);
col[i] = dg[u + i] = udg[n - i + u] = false;
g[u][i] = '.'; // 恢复现场
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0);
return 0;
}
方法2: 按照每个元素进行枚举
每个位置都有2种情况,放还是不放,总共就有n2
时间复杂度: O(2的n2次方), 打不出来了,见谅
原理图: 就类似这样画下去
思路: 按照每个位置放不放的步骤一点一点进行搜索。
code:
// 不同搜索顺序 时间复杂度不同 所以搜索顺序很重要!
#include <iostream>
using namespace std;
const int N = 20;
int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N]; // 因为是一个个搜索,所以加了row
// s表示已经放上去的皇后个数
void dfs(int x, int y, int s)
{
// 处理超出边界的情况, 这个是直接一行进行放还是不放, 一行走完了,跳到下一行开始
if (y == n) y = 0, x ++ ;
if (x == n) {
// x==n说明已经枚举完n^2个位置了
if (s == n) {
// s==n说明成功放上去了n个皇后
for (int i = 0; i < n; i ++ ) puts(g[i]);
puts("");
}
return;
}
// 分支1:放皇后
if (!row[x] && !col[y] && !dg[x + y] && !udg[x - y + n]) {
g[x][y] = 'Q';
row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
dfs(x, y + 1, s + 1);
row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
g[x][y] = '.';
}
// 分支2:不放皇后
dfs(x, y + 1, s);
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0, 0, 0);
return 0;
}
边栏推荐
- Network Security Learning - Information Collection
- 1.19.11. SQL client, start SQL client, execute SQL query, environment configuration file, restart policy, user-defined functions, constructor parameters
- UltraEdit-32 warm prompt: right association, cancel bak file [easy to understand]
- 浙江大学周亚金:“又破又立”的顶尖安全学者,好奇心驱动的行动派
- Imitate Tengu eating the moon with Avatar
- What is CGI, IIS, and VPS "suggested collection"
- VIM - own active button indent this command "suggestions collection"
- sscanf,sscanf_s及其相关使用方法「建议收藏」
- Highly paid programmers & interview questions. Are you familiar with the redis cluster principle of series 120? How to ensure the high availability of redis (Part 1)?
- 【实践出真理】import和require的引入方式真的和网上说的一样吗
猜你喜欢
AI 落地新题型 RPA + AI =?

CUDA Programming
数学分析_笔记_第10章:含参变量积分
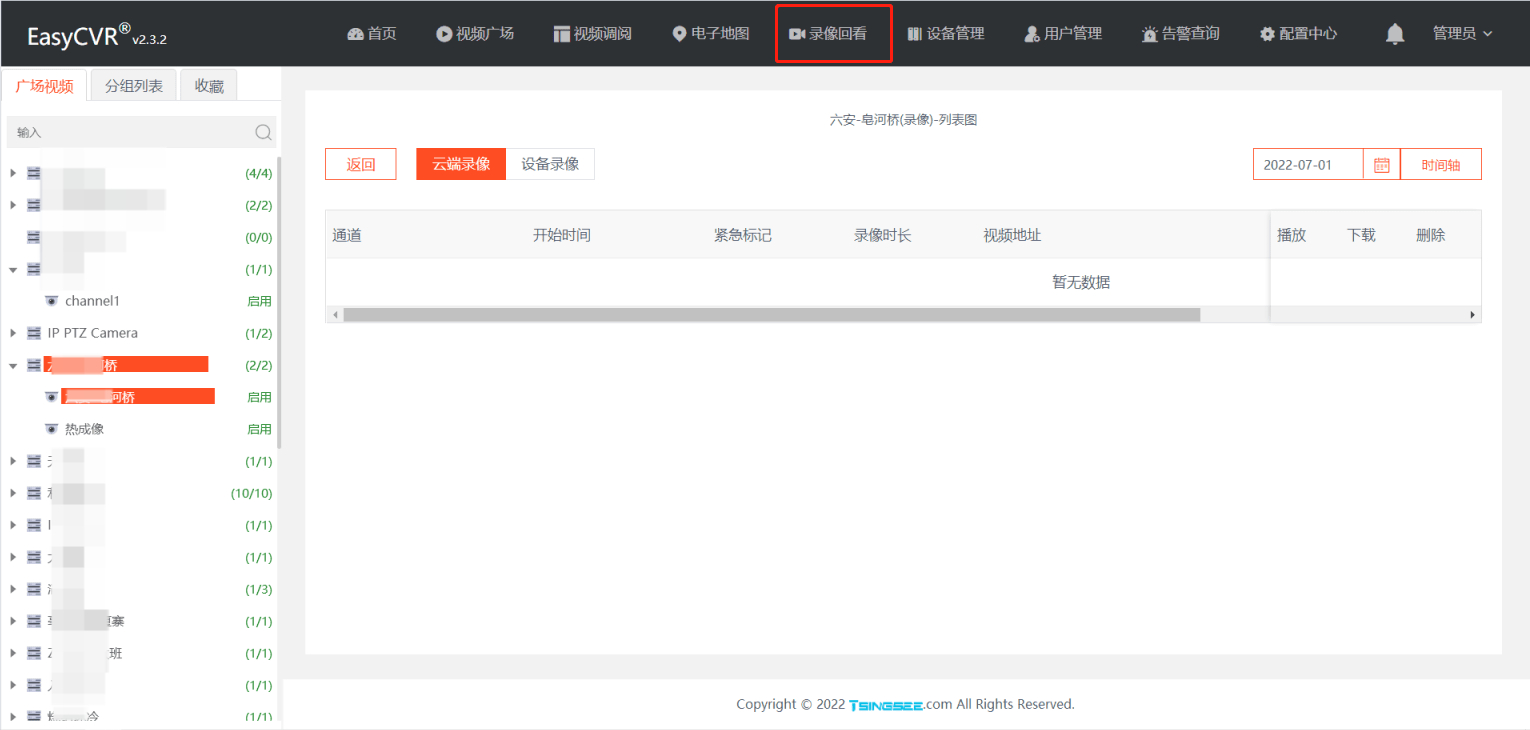
Fix the problem that the highlight effect of the main menu disappears when the easycvr Video Square is clicked and played

Common methods of list and map
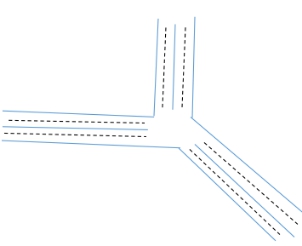
Analysis on urban transportation ideas of 2022 Zhongqing cup C
![[ArcGIS tutorial] thematic map production - population density distribution map - population density analysis](/img/82/8f5b6f388d5676cb7ff902ba80d9d2.jpg)
[ArcGIS tutorial] thematic map production - population density distribution map - population density analysis
![[OA] excel document generator: openpyxl module](/img/e3/e6a13a79ad9023cf263d1926a224b5.png)
[OA] excel document generator: openpyxl module

Dab-detr: dynamic anchor boxes are better queries for Detr translation

EasyCVR视频广场点击播放时,主菜单高亮效果消失问题的修复
随机推荐
JetBrain Pycharm的一系列快捷键
SSM+JSP实现企业管理系统(OA管理系统源码+数据库+文档+PPT)
Why does WordPress open so slowly?
什么是Web3
Win11远程桌面连接怎么打开?Win11远程桌面连接的五种方法
Win11图片打不开怎么办?Win11无法打开图片的修复方法
On the 110th anniversary of Turing's birth, has the prediction of intelligent machine come true?
EasyCVR无法使用WebRTC进行播放,该如何解决?
The worse the AI performance, the higher the bonus? Doctor of New York University offered a reward for the task of making the big model perform poorly
Comment les tests de logiciels sont - ils effectués sur le site Web? Testez la stratégie!
程序员上班摸鱼,这么玩才高端!
EasyCVR视频广场点击播放时,主菜单高亮效果消失问题的修复
What if the win11 screenshot key cannot be used? Solution to the failure of win11 screenshot key
Intel and Xinbu technology jointly build a machine vision development kit to jointly promote the transformation of industrial intelligence
Five years of automated testing, and finally into the ByteDance, the annual salary of 30W is not out of reach
機器人(自動化)課程的持續學習-2022-
[coded font series] opendyslexic font
Kotlin compose text supports two colors
ESG全球领导者峰会|英特尔王锐:以科技之力应对全球气候挑战
1.19.11. SQL client, start SQL client, execute SQL query, environment configuration file, restart policy, user-defined functions, constructor parameters