当前位置:网站首页>DDTL:远距离的域迁移学习
DDTL:远距离的域迁移学习
2022-08-04 01:11:00 【一瞬にして失う】
DDTL问题:目标域可以与源域完全不同。
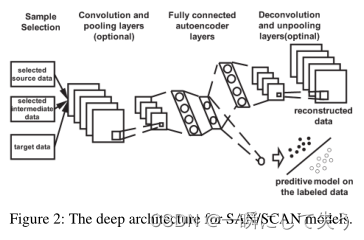
1、提出了一种选择性学习算法(SLA),以有监督自动编码器或有监督卷积自动编码器作为处理不同类型输入的基础模型。
2、SLA算法从中间域中逐渐选择有用的未标记数据作为桥梁,以打破两个远距离域之间传递知识的巨大分布差异。
迁移学习:从源领域借用知识来增强目标域学习能力的学习方法
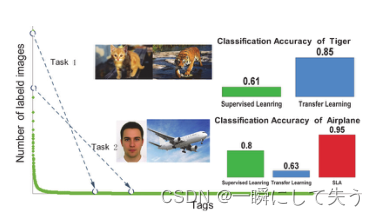
Task1:在猫和老虎图像之间传递知识。迁移学习算法比一些监督学习算法获得更好的性能。
Task2:在人脸和飞机图像之间传递知识。迁移学习算法失败,因为其性能比监督学习算法差。然而,当应用SLA算法时,获得了更好的性能。
1、DDTL问题定义
大小为
的源域标记数据:
;
大小为
的目标域标记数据:
;
多个中间域未标记数据的混合:
。
一个域对应于特定分类问题的一个概念或类别,例如从图像中识别人脸或飞机。
问题描述:假设源域和目标域中的分类问题都是二进制的。所有数据点都应位于同一特征空间中。设
、
和
分别是源域数据的边际分布、条件分布和联合分布;相对于目标域的三个分布为
,
,
;
是中间域的边际分布。在DDTL问题中:
;
;
。
目标:利用中间域中的未标记数据,在原本彼此距离较远的源域和目标域之间建立桥梁,并通过借助桥梁从源域迁移监督知识来训练目标域的准确分类器。
PS:并不是所有中间域中的数据都应该与源域数据相似,其中一些数据可能非常不同。因此,简单地使用所有中间数据来建造桥梁可能会失败。
2、SLA:选择性学习算法
2.1自动编码器及其变体
自动编码器是一种无监督前馈神经网络,具有输入层、一个或多个隐藏层和输出层,它通常包括两个过程:编码和解码。
输入:
;
编码函数:
对其进行编码以将其映射到隐藏表示;
解码函数:
进行解码以重构x。
自动编码器的过程可以总结为:
编码:
;
解码:
.
其中
是近似于原输入x的重构输入。通过最小化所有训练数据上的重构误差,即
2.2通过重构误差进行实例选择
在实践中,由于源域和目标域相距较远,可能只有一部分源域数据对目标域有用,中间域的情况相似。因此,为了从中间域中选择有用的实例,并从源域中移除目标域的相关实例,通过最小化源域和中间域中所选实例以及目标域中所有实例的重建误差来学习一对编码和解码函数。要最小化的目标函数公式如下:
、
∈ {0,1}:源域中第i个实例和中间域中第j个实例的选择指示符。当值为1时,将选择相应的实例,否则将取消选择。
:
和
上的正则化项,通过将
和
的所有值设置为零来避免一些不重要的解。将其定义为:
最小化该项等同于鼓励从源域和中间域中选择尽可能多的实例。两个正则化参数
和
控制该正则化项的重要性。
2.3辅助信息的阐述
在学习不同领域的隐藏表示时纳入辅助信息。
源域和目标域:数据标签可以用作辅助信息;
中间域:没有标签信息。
将中间域上的预测视为辅助信息,并使用预测的置信度来指导隐藏表示的学习。具体而言,我们建议通过最小化以下函数将辅助信息纳入学习:
:是输出分类概率的分类函数;
g(·):定义为
,其中0≤ z≤ 1;
将
用于选择中间域中的高预测置信度的实例。
2.4总体目标函数
DDTL的最终目标函数如下:
其中
;Θ表示函数
、
和
的所有参数。
使用块坐标decedent(BCD)方法,在每次迭代中,在保持其他变量不变的情况下,顺序优化每个块中的变量。
在
中选择具有低重建误差和低训练损失;在
中选择具有低重建误差和低训练损失。
深度学习体系结构如下图所示。
3、总结
本文研究了一个新的DDTL问题,其中源域和目标域距离较远,但可以通过一些中间域连接。为了解决DDTL问题,提出了SLA算法,从中间域中逐渐选择未标记数据,以连接两个距离较远的域。
边栏推荐
- 静态文件快速建站
- Google Earth Engine - Calculates the effective width of rivers using publicly available river data
- nodejs+npm的安装与配置
- Electronics manufacturing enterprise deployment WMS what are the benefits of warehouse management system
- 2022 China Computing Power Conference released the excellent results of "Innovation Pioneer"
- LDO investigation
- 互斥锁、读写锁、自旋锁,以及原子操作指令xaddl、cmpxchg的使用场景剖析
- How to copy baby from Taobao (or Tmall store) through API interface to Pinduoduo interface code docking tutorial
- 数组_滑动窗口 | leecode刷题笔记
- Linux安装mysql最简单教程(一次成功)
猜你喜欢
Installation and configuration of nodejs+npm

WMS仓储管理系统能解决电子行业哪些仓库管理问题
静态文件快速建站
【store商城项目01】环境准备以及测试
600MHz频段来了,它会是新的黄金频段吗?
typescript58 - generic classes

The 600MHz band is here, will it be the new golden band?
LeetCode第三题(Longest Substring Without Repeating Characters)三部曲之三:两次优化
typescript55-泛型约束

快速入门EasyX图形编程
随机推荐
Mvc, Mvp and Mvvm
KunlunBase 1.0 发布了!
优秀的测试/开发程序员,是怎样修炼的?步步为营地去执行......
boot issue
XSS - Bypass for loop filtering
MongoDB数据接入实践
Apache DolphinScheduler新一代分布式工作流任务调度平台实战-中
【虚拟户生态平台】虚拟化平台安装时遇到的坑
Google Earth Engine - Calculates the effective width of rivers using publicly available river data
The 600MHz band is here, will it be the new golden band?
appium软件自动化测试框架
Demand analysis of MES management system in electronic assembly industry
Analysis: What makes the Nomad Bridge hack unique
GraphQL背后处理及执行过程是什么
jmeter分布式压测
C# WPF设备监控软件(经典)-下篇
C 学生管理系统 显示链表信息、删除链表
观察者模式
nodejs+npm的安装与配置
typescript48 - type compatibility between functions
 的
的 ;
; 的
的 ;
; 。
。 、
、 和
和 分别是源域数据的
分别是源域数据的 ,
, ,
, ;
; 是中间域的边际分布。在DDTL问题中:
是中间域的边际分布。在DDTL问题中: ;
; ;
; 。
。 ;
; 对其进行编码以将其映射到隐藏表示;
对其进行编码以将其映射到隐藏表示; 进行解码以重构x。
进行解码以重构x。 ;
; .
. 是近似于原输入x的重构输入。通过最小化所有训练数据上的重构误差,即
是近似于原输入x的重构输入。通过最小化所有训练数据上的重构误差,即

 、
、 ∈ {0,1}:
∈ {0,1}: :
: 和
和 上的正则化项,通过将
上的正则化项,通过将
 和
和 控制该正则化项的重要性。
控制该正则化项的重要性。
 :是输出分类概率的分类函数;
:是输出分类概率的分类函数; ,其中0≤ z≤ 1;
,其中0≤ z≤ 1; 用于选择
用于选择
 ;Θ表示函数
;Θ表示函数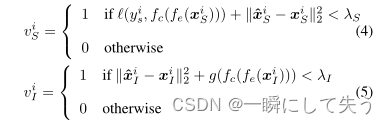
 中选择具有低重建误差和低训练损失。
中选择具有低重建误差和低训练损失。