当前位置:网站首页>哈夫曼树(暑假每日一题 15)
哈夫曼树(暑假每日一题 15)
2022-08-04 17:46:00 【sweetheart7-7】
给定 N N N 个权值作为 N N N 个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
现在,给定 N N N 个叶子结点的信息,请你构造哈夫曼树,并输出该树的带权路径长度。
相关知识:
1、路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为 1 1 1,则从根结点到第 L L L 层结点的路径长度为 L − 1 L−1 L−1。
2、结点的权及带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
3、树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为 W P L WPL WPL。
输入格式
第一行包含整数 N N N,表示叶子结点数量。
第二行包含 N N N 个整数,表示每个叶子结点的权值。
输出格式
输出一个整数,表示生成哈夫曼树的带权路径长度。
数据范围
2 ≤ N ≤ 1000 , 2≤N≤1000, 2≤N≤1000,
叶子结点的权值范围 [ 1 , 100 ] [1,100] [1,100]。
输入样例:
5
1 2 2 5 9
输出样例:
37
#include<iostream>
#include<queue>
#include<cstring>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 2010;
int n;
int a[N], l[N], r[N];
priority_queue<PII, vector<PII>, greater<PII>> q;
int get(int u, int d){
if(l[u] == -1 && r[u] == -1) return a[u] * d;
return get(l[u], d + 1) + get(r[u], d + 1);
}
int main(){
memset(l, -1, sizeof l);
memset(r, -1, sizeof r);
cin >> n;
for(int i = 0; i < n; i++)
cin >> a[i], q.push({
a[i], i});
PII t1, t2;
while(q.size() > 1){
t1 = q.top(), q.pop();
t2 = q.top(), q.pop();
int s = t1.x + t2.x;
l[n] = t1.y, r[n] = t2.y;
q.push({
s, n});
n++;
}
PII root = q.top();
cout << get(root.y, 0) << endl;
return 0;
}
边栏推荐
- 【技术笔记】let 和 var和const的异同
- 设置表头颜色
- 租房小程序登顶码云热门
- Thrift IDL示例文件
- pyhon爬虫之爬取图片(亲测可用)
- Catering Supply Chain Management System
- (一)、线性表的顺序存储结构链式存储结构
- The second step through MySQL in four steps: MySQL index learning
- 】 【 LeetCode daily one problem - 540. The order of a single element of the array
- Introduction of three temperature measurement methods for PT100 platinum thermal resistance
猜你喜欢
Clearance sword refers to Offer——The sword refers to Offer II 010. and the sub-array of k
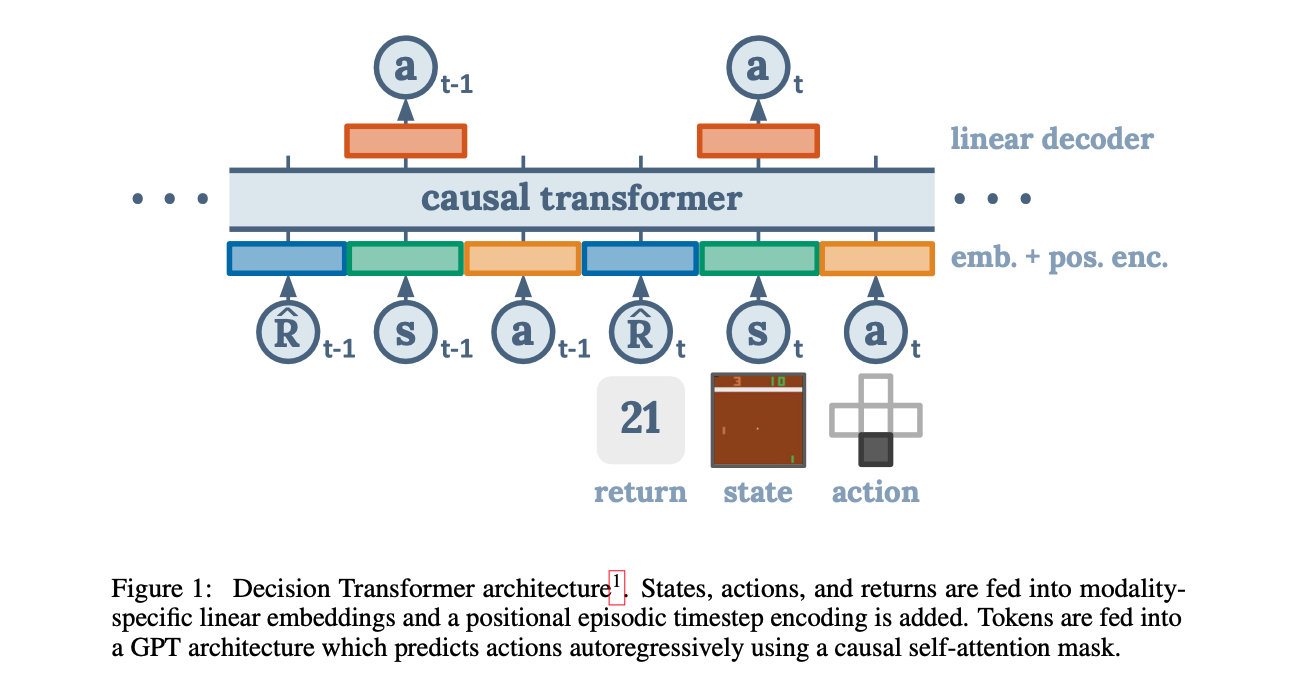
【论文阅读】Decision Transformer: Reinforcement Learning via Sequence Modeling

LeetCode Question of the Day - 1403. Minimum Subsequence in Non-Increasing Order

Cholesterol-PEG-DBCO,CLS-PEG-DBCO,胆固醇-聚乙二醇-二苯基环辛炔科研试剂

Kotlin挂起函数原理是什么
LVS+Keepalived群集

使用scikit-learn计算文本TF-IDF值

88. (the home of cesium) cesium polymerization figure
【无标题】

mysqlbinlog 超过500g自动删除,保留7个,求大深给个版本
随机推荐
小程序笔记1
LeetCode Question of the Day - 1403. Minimum Subsequence in Non-Increasing Order
init和destory方法
网络靶场监控系统的安全加固纪实(1)—SSL/TLS对日志数据加密传输
软件测试高频面试题真实分享/网上银行转账是怎么测的,设计一下测试用例。
OpenInfra Days China 2022 | SelectDB to share with you the Apache Doris in Internet advertising business practices
Clearance sword refers to Offer——The sword refers to Offer II 010. and the sub-array of k
JS中null与undefined的异同点
【 Gazebo introductory tutorial] speak the second model library into robot modeling and visualization (editor) model
Cholesterol-PEG-DBCO,CLS-PEG-DBCO,胆固醇-聚乙二醇-二苯基环辛炔科研试剂
容器化 | 在 NFS 备份恢复 RadonDB MySQL 集群数据
C# Sqlite database construction and use skills
《机器学习理论到应用》电子书免费下载
R语言dplyr包group_by函数和summarise_at函数计算dataframe计算不同分组的计数个数和均值、使用%>%符号将多个函数串起来
Thrift安装配置
租房小程序登顶码云热门
Cholesterol-PEG-Maleimide,CLS-PEG-MAL,胆固醇-聚乙二醇-马来酰亚胺一种修饰性PEG
OpenInfra Days China 2022|SelectDB与你共享 Apache Doris 在互联网广告业务中的实践
darknet源码阅读笔记-02-list.h和lish.c
clickhouse 上下线表