当前位置:网站首页>[线性代数] 1.3 n阶行列式
[线性代数] 1.3 n阶行列式
2022-07-06 14:21:00 【Michael_Lzy】
先研究三阶行列式:
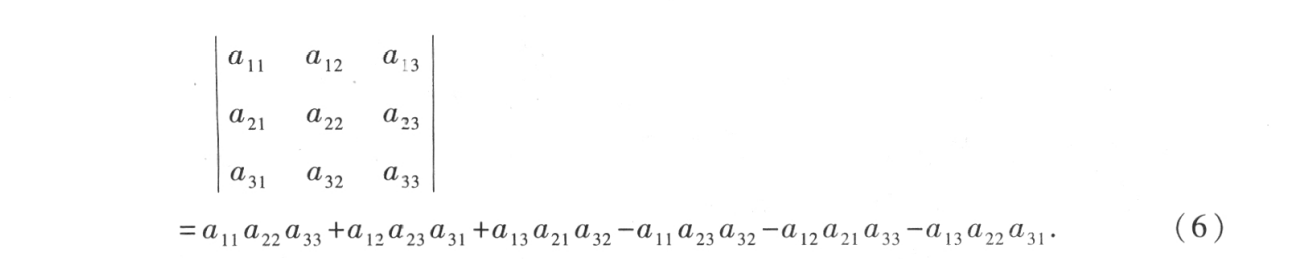
容易看出:
1) (6)式的每一项都恰好是三个元素的乘积,这三个元素位于不同行、不同列。
因此任一项除正负号外都可以写成 .
.
这里每一项的第一个下标(行标)排成标准次序123。
即:![]()
而每一项的第二个下标(列标),排成p1p2p3,它是1,2,3三个数的某个排列。这样的排列共有6种,对应(6)式共含6项。
2)各项的正负号与列标的排列对照
带正号的三项列标排列是123,231,312.(都是偶排列)
![]()
带负号的三项列标排列是132,213,321.(都是奇排列)
经计算可知前三个排列都是偶排列,而后三个排列都是奇排列。
因此,各项所带的正负号可以表示为 ,其中t为列标排列的逆序数。
,其中t为列标排列的逆序数。
总之,三阶行列式可以写成:
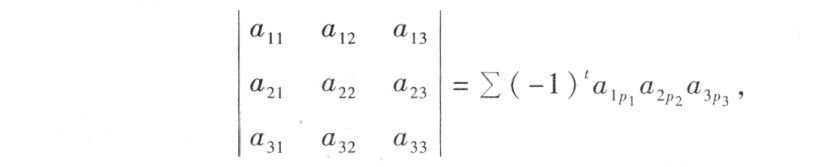
其中t为排列 p1p2p3 的逆序数,∑表示对所有排列种类取和。
把行列式推广到一般形式:
设有 个数,排成n行n列的数表:
个数,排成n行n列的数表:
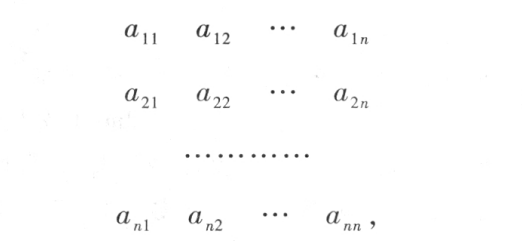
作出表中位于不同行不同列的 n 个数的乘积,并冠以符号 ,得到形如
,得到形如
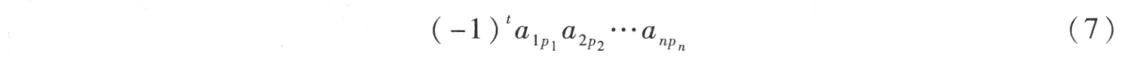
其中p1p2...pn为自然数1,2...,n的一个排列,t为这个排列的逆序数。
由于这样的排列共有n!个,因而形如(7)式的项共有n!项。
所有这n!项的代数和
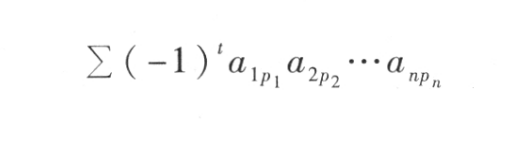
称为n阶行列式,记作:

简记作det( ),其中数
),其中数 为行列式的(i,j)元。
为行列式的(i,j)元。
当n=1时,一阶行列式|a|=a,注意不要与绝对值号弄混。
主对角线以下的元素都为0的行列式叫做上三角行列式。
主对角线以上的元素都为0的行列式叫做下三角行列式。
主对角线以上和以下的元素都为0的行列式叫做对角行列式。
边栏推荐
- GPS从入门到放弃(十五)、DCB差分码偏差
- Intelligent online customer service system source code Gofly development log - 2 Develop command line applications
- 3DMax指定面贴图
- 2500个常用中文字符 + 130常用中英文字符
- Sparkshuffle process and Mr shuffle process
- Aggregate function with key in spark
- [asp.net core] set the format of Web API response data -- formatfilter feature
- 二叉(搜索)树的最近公共祖先 ●●
- 中国固态氧化物燃料电池技术进展与发展前景报告(2022版)
- 关于程序员的职业操守,从《匠艺整洁之道》谈起
猜你喜欢
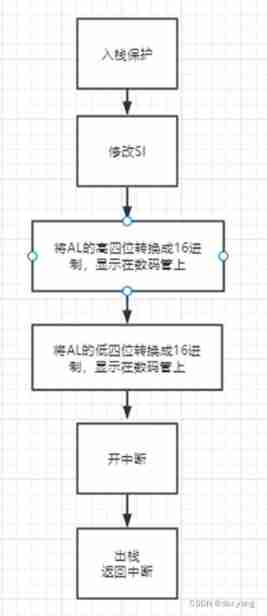
Assembly and Interface Technology Experiment 6 - ADDA conversion experiment, AD acquisition system in interrupt mode

用aardio写一个旋转验证码标注小工具

Oracle-控制文件及日志文件的管理

【MySQL】Online DDL详解
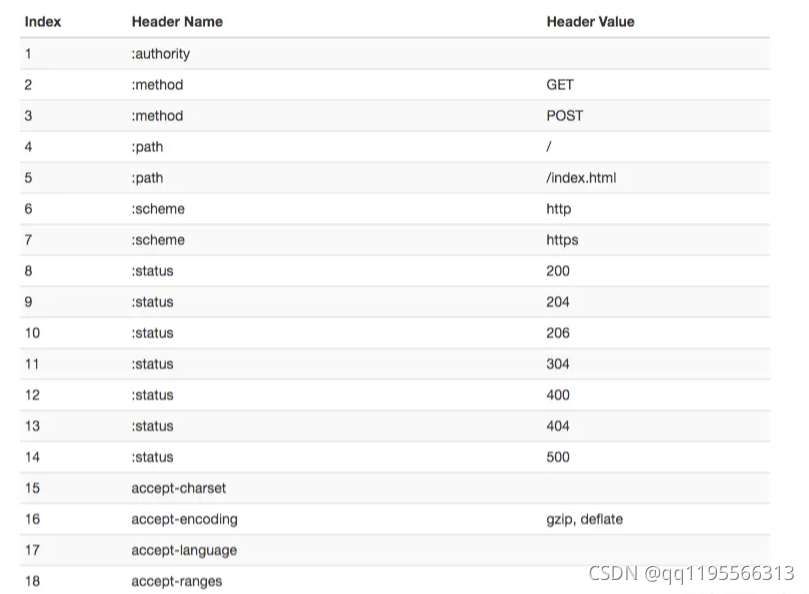
小满网络模型&http1-http2 &浏览器缓存

How does the uni admin basic framework close the creation of super administrator entries?
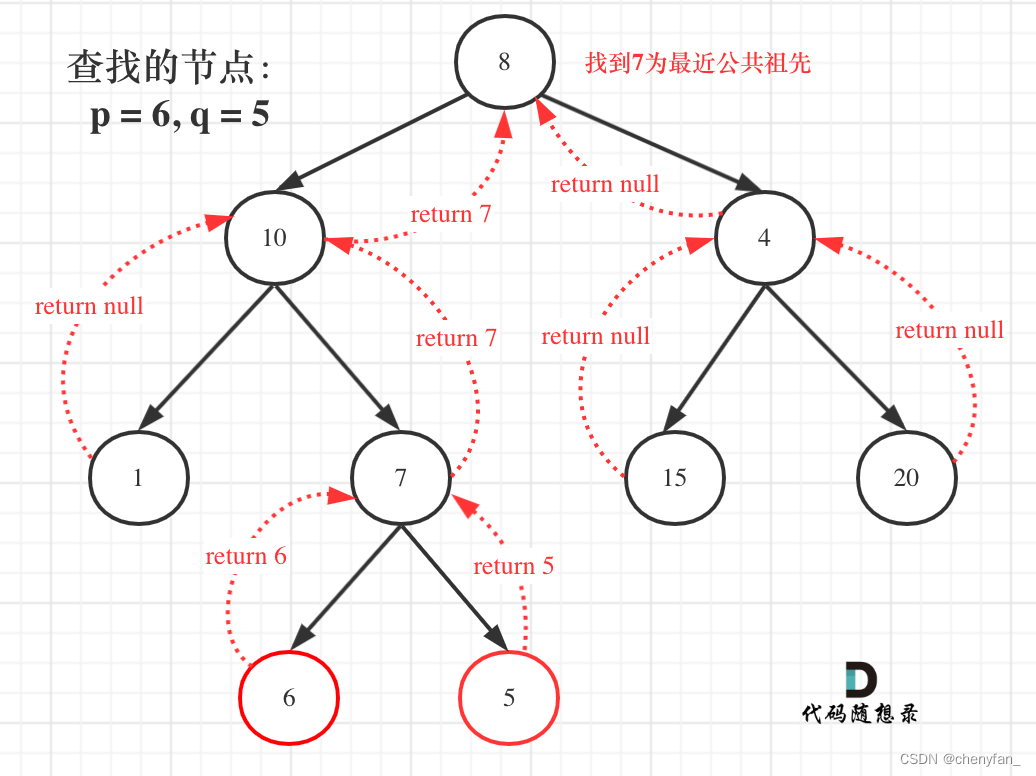
二叉(搜索)树的最近公共祖先 ●●

Unity3D学习笔记6——GPU实例化(1)
LeetCode刷题(十一)——顺序刷题51至55
![[10:00 public class]: basis and practice of video quality evaluation](/img/d8/a367c26b51d9dbaf53bf4fe2a13917.png)
[10:00 public class]: basis and practice of video quality evaluation
随机推荐
GNN,请你的网络层数再深一点~
GNN, please deepen your network layer~
Yyds dry goods inventory C language recursive implementation of Hanoi Tower
Management background --2 Classification list
Unity3d Learning Notes 6 - GPU instantiation (1)
搜素专题(DFS )
[Chongqing Guangdong education] Tianjin urban construction university concrete structure design principle a reference
中国VOCs催化剂行业研究与投资战略报告(2022版)
Oracle性能分析3:TKPROF简介
i.mx6ull搭建boa服务器详解及其中遇到的一些问题
[sdx62] wcn685x will bdwlan Bin and bdwlan Txt mutual conversion operation method
设置状态栏样式Demo
C#實現水晶報錶綁定數據並實現打印4-條形碼
[leetcode daily clock in] 1020 Number of enclaves
GPS from getting started to giving up (XX), antenna offset
2020 Bioinformatics | GraphDTA: predicting drug target binding affinity with graph neural networks
The golden age of the U.S. technology industry has ended, and there have been constant lamentations about chip sales and 30000 layoffs
LeetCode学习记录(从新手村出发之杀不出新手村)----1
十二、启动流程
中国1,4-环己烷二甲醇(CHDM)行业调研与投资决策报告(2022版)