Leetcode+ 81 - 85 monotone stack topic

Search rotation sort array II

Algorithm tags ： Array 、 Two points search

 

Refer to the first 33 topic

LeetCode+ 31 - 35 Two sub topics _ Xiaoxuecai's blog -CSDN Blog

( Linear scanning ) O(n)

Refer to the explanation of the question

LeetCode 81 Search in Rotated Sorted Array II - AcWing

This problem is similar to that in No 33 topic , The difference is that the array in this problem may contain the same elements .
At present, the worst time complexity of the conceivable dichotomy is O(n), So we simply did linear scanning ^^

Time complexity analysis ： The whole array is scanned only once , So time complexity is O(n)

class Solution {
public:
    bool search(vector<int>& nums, int target) {
        for (auto &v : nums)
            if (v == target)
                return true;
        return false;
    }
};

With the first 33 The difference between questions is that there may be repeated elements , That means that the number before the first paragraph and after the second paragraph may be the same

 

If there is no such situation , We can divide the dividing point in two , Why can we divide the dividing point in two ？

Suppose no first paragraph is equal to the next one , Suppose there is no later paragraph , There will be later numbers that are strictly smaller than the number in the first paragraph , This property is binary , Any property with duality can distinguish the dividing point

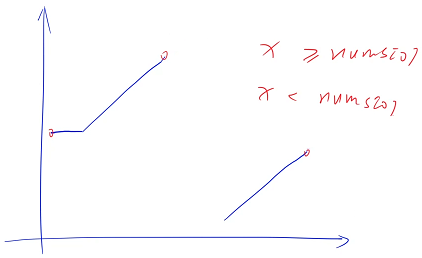
But this question does not have the above properties , It is possible that the latter paragraph is equal to the first paragraph , The nature of this paragraph is not tenable

When we are about a x, If it is greater than or equal to nums[ 0 ] Words , It is not certain whether it is at the beginning or at the end , So we can't divide , In order to make it binary, we can do some optimization , But in the worst case, the time complexity cannot be optimized

Just delete the part with the same beginning or end first , Only the end is the same as the beginning , Just delete the end , So you can split in two

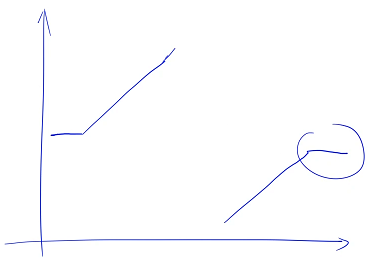
Because the deleted scores are repeated in the front , The deleted numbers are all duplicate numbers , So it will not affect our judgment , It does not affect the accuracy of the answer , But after we delete all the repeated numbers , We can split in two , Into the first 33 Problem solving

The question requires to judge whether the given target value exists in the array . If nums There is a target value in target , Then return to true , Otherwise return to false .

The idea is to remove the equal parts of the back and the front first , After removing it, divide it into two parts first , After the dividing point , Divide it in two in each paragraph , Just see if there is an answer

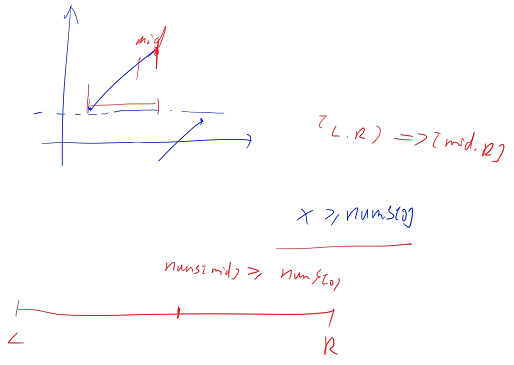
while (R >= 0 && nums[R] == nums[0]) R- -; Will execute n Time , The worst case of time complexity is O( n )

class Solution {
public:
    bool search(vector<int> &nums, int target) {
        // Array is empty and returns  false
        if(nums.empty()) return false;
        // Define the end point 
        int R = nums.size() - 1;
        // When the end point is greater than  0  also  nums[R]  If it is equal to the beginning, you can delete this number 
        while (R >= 0 && nums[R] == nums[0]) R--;
        // If you find that the entire array has been deleted   All numbers of the whole array are the same 
        if (R < 0) 
        // Because all numbers are the same, they are equal to nums[0], Just judge nums[0] Is it equal to target That's all right. 
        return nums[0] == target; 
        // Delete the same part at the end   Into the first 33 Problem solving 
        // Bisection dividing point 
        int l = 0, r = R;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            // If  nums[mid]  Greater than or equal to  nums[0]  Explain that it is in the first half   The dividing point to be bisected is actually the last number that satisfies this property 
            if (nums[mid] >= nums[0]) l = mid;
            else r = mid - 1;
        }
        // Judge after getting the dividing point target Which part does it belong to , If target >= nums[0], explain target It's in the first part , The range of two points should be from 0 To the dividing point just now 
        if (target >= nums[0]) l = 0,r = r;
        // Otherwise, the interval of two points is in the right half   It should be the next position of the dividing point just now 
        else l++, r = R;
        // Last in l ~ R Between two points to find whether there is target This value is enough 
        while (l < r) {
            int mid = l + r >> 1;
            // Two points greater than or equal to target The first number of , If nums[mid] > = target, Explain that the answer is mid Left or mid Location 
            if (nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        // Finally, judge nums[r] Is it equal to target That's all right. 
        return nums[r] == target;
    }
};

Delete duplicate elements from the sort list II

Algorithm tags ： Linked list 、 Double pointer

 

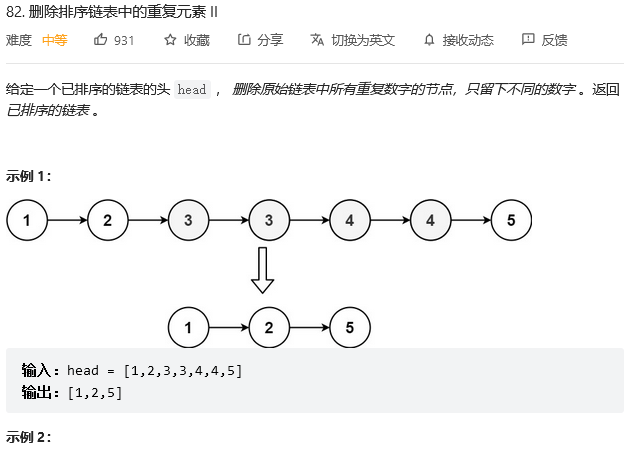
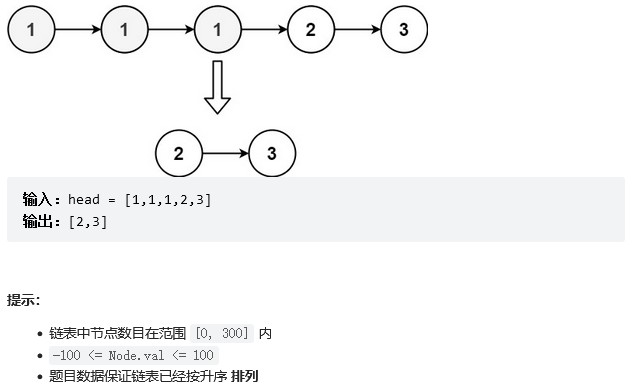
Give us a sort list , Sorting a linked list means that all the same elements are arranged together , Delete all repeated elements inside , As long as an element appears twice or more, delete it , Note that it is not to delete the repeated elements, leaving only one

Simulation example

3 Repeat , Two 3 All have to be deleted , Similar to ancient punishment " Continuous sitting "

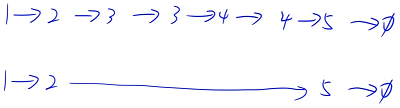
Sorting a linked list means that all adjacent elements are next to each other , When traversing to the position of a certain point , I want to see if the length of the continuous equal part behind this point is greater than 1

Look at the back 4 How many are there , If 4 The number of is greater than 1, You need to delete the following , If 4 There are only 1 There is no need to delete , The next thing to do is to count how many there are 4, It can be regarded as a double pointer algorithm , Scan the current continuous equal segment , First, use a pointer to record the first number of a paragraph , Another pointer , Start with the second number in the next paragraph , As long as the second pointer and the first pointer point to the same number , Just move the second pointer back one bit , Until it is not equal or empty . When we move to 5 Found that 5 and 4 Dissimilarity , Stop moving , In this way, we can find this equal interval

This section is equal to an interval that is left closed and right open , How to judge how many elements there are in the current paragraph ？

Just judge whether the next position of the first pointer is equal to the second pointer , If there is only one number in this paragraph , The next position of the first pointer is the position of the second pointer , If there is more than one number in this paragraph , It means that the next position of the first pointer and the position of the second pointer are not equal , In this way, we can judge how many elements there are in this paragraph

① If there is only one number in the next paragraph , Just move the first pointer back one bit

② If there is more than one number in the next paragraph , You need to delete all the numbers in the next paragraph , Put the last node's next Just point to the second pointer directly

Every time the pointer points to the previous number of a certain section , The previous number of the head node should also exist , In order to facilitate the establishment of a virtual head node

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        auto dummy = new ListNode(-1);
        // Of the virtual head node  next  The pointer is equal to the real head node 
        dummy->next = head;
        // Define a pointer to the front of a paragraph 
        auto p = dummy;
        // When there is the next paragraph   Find the second one in the next paragraph every time 
        while(p->next) {
            auto q = p->next->next;
            // The second number of the next paragraph exists and the value of the second number of the next paragraph is equal to the value of the first number of the next paragraph   The second pointer goes straight back 
            while(q && q->val == p->next->val) q = q->next;
            // If the first pointer  next  If it's equal to  q  Words , Explain that there is only one number in the next paragraph 
            if(p->next->next == q)
            //p  Just go to the next position 
            p = p->next;
            // Otherwise, delete the next paragraph 
            else p->next = q;
        }
        // Return to the next position of the virtual head node 
        return dummy->next;
    }
};

Delete duplicate elements from the sort list

Algorithm tags ： Linked list

 

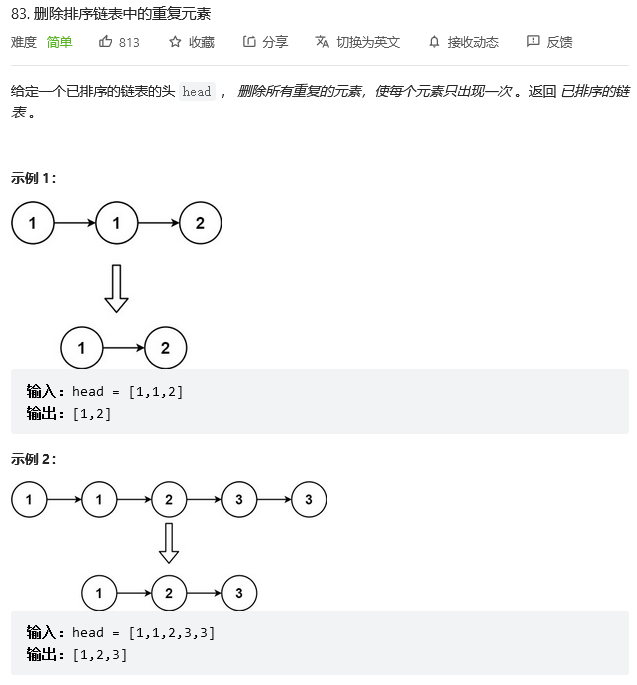
Because the linked list is sorted , Explain that all the same elements are arranged together

For the same number in a certain paragraph , In order to keep only one , We stipulate that the first item should be reserved for the same number of each item

Simulation example

There's a lot of 2, Choose only the first 2, There's a lot of 3, Choose only the first 3 , Next, let's see how to store the first number of each paragraph . First , The first number of the whole linked list must be stored , Because it must be the first number of a certain paragraph , After the first number is stored , Then traverse from the second number of the whole linked list , Each time, judge whether the number currently traversed is the first number of this section , If it is the first number in this paragraph , Just move this node , If not, skip

How to judge whether the current number is the first number in this paragraph ？

Just check whether the current number is the same as the last number of the linked list we stored , You can find 2 ！= 1, So this 2 It must be the first 2, Put this 2 Move over here , Continue to look back at the next number 2 == 2, explain 2 It already exists , Just skip . Let's look at 3, because 3 ！= 2, So this 3 Is the first 3, Put this 3 Move over here , And so on , At last, just add a null pointer

/**
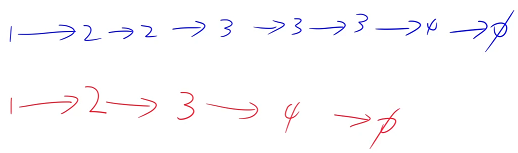
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        // It's empty   Returns an empty 
        if(!head) return head;
        // use cur Represents the last node of the new linked list  
        auto cur = head;
        // Traverse from the second point of the original linked list 
        for(auto p = head->next; p; p = p->next)
            // Each time, compare whether the current node is the same as the last node of the new linked list 
            if(p->val != cur->val)
                // If not, move the current point to the new linked list cur Last  p It is the last point of the new linked list 
                 cur = cur->next = p;
        // Finally, point the tail node of the new linked list to null 
        cur->next = NULL;       
        // Return to the new list 
        return head;
    }
};

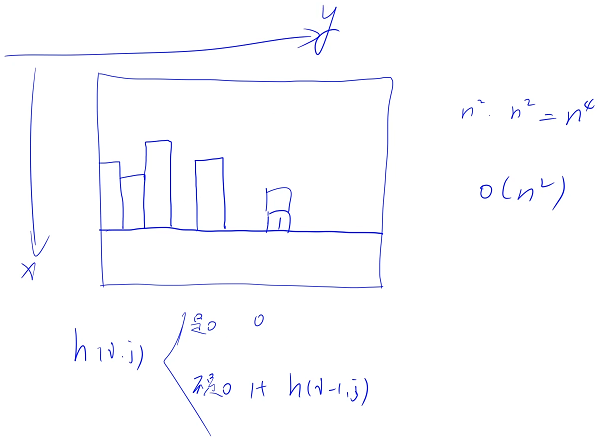
The largest rectangle in the histogram

Algorithm tags ： Stack 、 Array 、 Monotonic stack

 

 

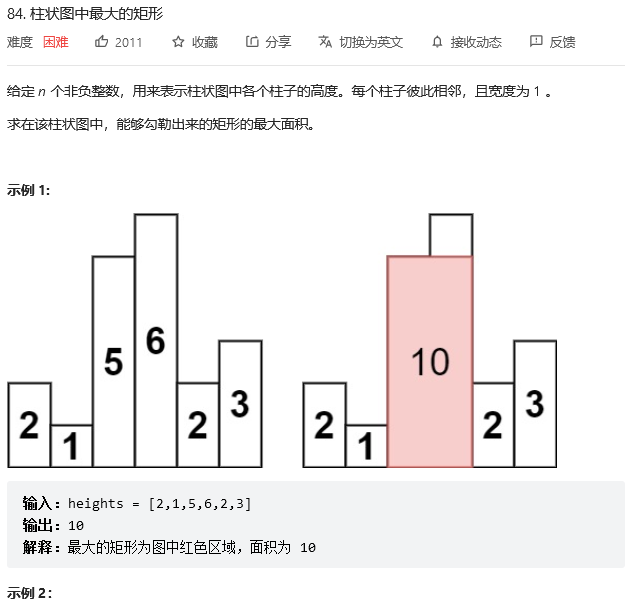
Classic application of monotone stack

Linked list and adjacency list 、 Stack and queue 、 Monotonic stack 、 A monotonous queue 、kmp Algorithm _ Xiaoxuecai's blog -CSDN Blog

Monotone stack can solve the problem of finding the subscript of the number smaller than it on the left of each number in a sequence , Next, let's see if there is such a model in some topics

The title gives n Vertical bar , this n The width of each vertical bar is 1, The height is given ,n A vertical bar is located on a coordinate axis , The two are close together , We need to find out the largest rectangle in the vertical bar ？

This topic is actually an enumeration plus optimization problem , Next, think about how to enumerate all the situations , When enumerating, you can enumerate many things , You can enumerate the left and right boundaries of the rectangle , It takes two cycles , The time complexity is O(n^2), When the left and right boundaries are determined , Look at the maximum height

We can also consider enumerating the upper boundary of the rectangle , The upper boundary of the rectangle must be stuck by a vertical line , It can't be in the middle of the vertical line , For example, we want to take a look at 5 This side is a rectangle with an upper boundary , What is the maximum left and right width → What is the maximum left ？ What is the maximum right ？

The left and right boundaries are the positions of the first lower rectangle on the left and right sides of this vertical line

The area is the height of the upper boundary multiplied by the distance between the left and right boundaries

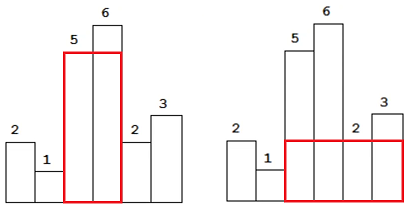
We can enumerate the upper boundary , After we enumerate the upper boundary , Just ask for each upper boundary , With this side as the upper boundary , Count to the left the farthest place ？ And the farthest place to the right ？

The farthest place to the left is actually to find out the position of the column shorter than it on the left of the vertical bar

The farthest place to the right is actually to find out the position of the shorter column on the right of the vertical bar that is closest to it

Then we can find the maximum area

In essence, it is to find the position of the first smaller number on the left of each number , And the position of the first smaller number on the right of each number

Scan from left to right to find the first smaller one on the left , Then scan it from right to left , Just find the first smaller one on the right

How to use monotone stack to find the first number smaller than it on the left of each number ？

When scanning from left to right , Record all the numbers in the stack , Abscissa is its subscript , The ordinate is the size of the number , How to find the first smaller number on the left of the current number every time ？ We scan from the top of the stack , Until the first number smaller than it is scanned

Optimize

On the right is the top of the stack , On the left is the bottom of the stack , Suppose the number on the left ① Than the number on the right ② Big , If there is a ratio ① It must be bigger than ② Big , and ② stay ① To the right of , as long as ② There is ,① It will not be used , You can put the ① Delete , As long as the previous number is larger than the latter , You can delete the previous number , After this deletion , This stack becomes a monotonous stack

For the current number , When looking for the first number smaller than this number , We can start from the top of the stack , As long as the stack top element is larger than the current number, it means that the stack top element is useless , The top element of the stack can be deleted , Until the element at the top of the stack is smaller than the current element , Add the current number to the stack , Plus before , The top of the stack is the number of the current number

Time complexity analysis

Each number will only enter the stack once , And it only comes out of the stack once , So the time complexity of the whole process is O(n)

class Solution {
public:
    int largestRectangleArea(vector<int>& h) {
        // use  n  Represents the maximum length 
        int n = h.size();
        // Define the position of the first smaller number to the left of each number 、 The position of the first smaller number on the right of each number 
        vector<int> left(n),right(n);
        // Define a stack 
        stack<int> stk;
        // Scan each number from front to back 
        for(int i = 0; i < n;i ++ ) {
            // When there are elements in the stack   And the element at the top of the stack is greater than or equal to the current element   Just delete the top element of the stack 
            while(stk.size() && h[stk.top()] >= h[i]) stk.pop();
            // If the stack is empty , It means that any number is larger than the current one , The left boundary can take the leftmost side , Assign it to -1
            if(stk.empty()) left[i] = -1;
            // otherwise left[i] Equal to the subscript of the element at the top of the stack 
            else left[i] = stk.top();
            // Insert the current element into the stack 
            stk.push(i);
        }
        // Empty the stack 
        stk = stack<int>();
        // Scan each number from back to left 
        for(int i = n - 1; i >= 0; i-- ) {
            // When there are elements in the stack   And the element at the top of the stack is greater than or equal to the current element   Just delete the top element of the stack 
            while(stk.size() && h[stk.top()] >= h[i]) stk.pop();
            // If the stack is empty 
            if(stk.empty()) right[i] = n;
            // otherwise right[i] Equal to the subscript of the element at the top of the stack 
            else right[i] = stk.top();
            // Insert the current element into the stack 
            stk.push(i);
        }
        // Traverse each upper boundary   Update answers 
        int res = 0;
        // Understand in combination with boundary conditions 
        for(int i = 0; i < n; i++ ) {
            res = max(res,h[i] * (right[i] - left[i] - 1));
            cout << "h[" << i << "]:"<< h[i] << "\t" << "l[" << i 
            << "]:" << left[i] << "\t" << "r[" << i << "]:" << right[i] << "\t";
        }
        return res;
    }
};

stdout
h[0]:2	l[0]:-1	r[0]:1	h[1]:1	l[1]:-1	r[1]:6	h[2]:5	l[2]:1	r[2]:4	
h[3]:6	l[3]:2	r[3]:4	h[4]:2	l[4]:1	r[4]:6	h[5]:3	l[5]:4	r[5]:6	

The largest rectangle

Algorithm tags ： Stack 、 Array 、 Dynamic programming 、 matrix 、 Monotonic stack

 

 

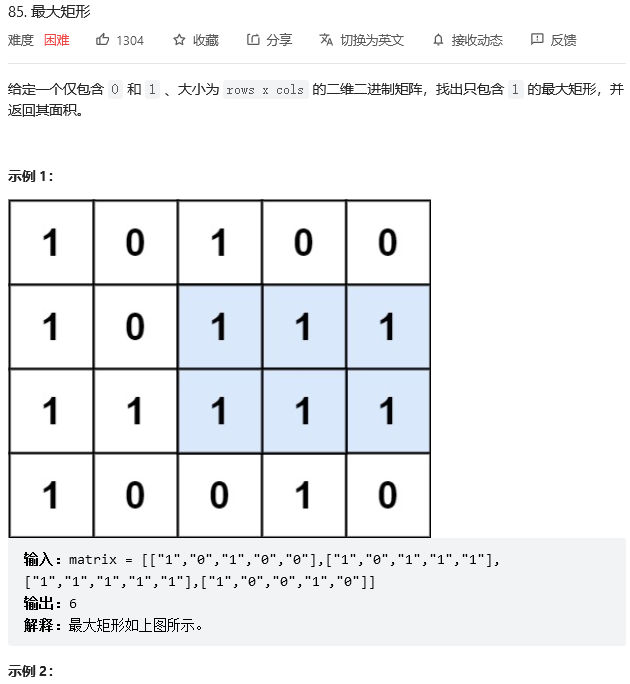
Give us one 0、1 matrix , To be in this 0、1 The largest one found in the matrix only contains 1 The rectangular , You need to consider how to enumerate all the schemes , In the worst case, you can enumerate the coordinates of the upper left corner first, and then the coordinates of the lower right corner , Then judge whether the rectangle is full of 1, The time complexity is O(n^6), Judge whether the rectangle is full of 1 You can use prefixes and optimizations , The time complexity is O(n^4)

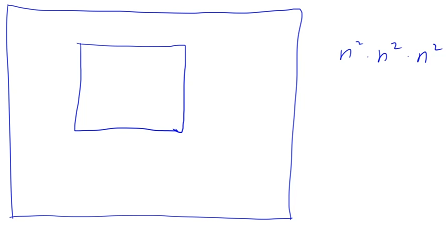
The last question is to give us a pile of pillars , Find the largest rectangle inside the column , This question is about how to find that pile of columns

With the help of the model of the previous question , First enumerate the lower boundary of the rectangle , Then preprocess how many consecutive cells are up in each grid 1, Note that this is the maximum height , It's full of 0, The pillars are all 1, Of course, the height of the column is 0 The situation of

After the lower boundary is determined , To find the largest rectangle in this pile of columns , Just find out this pile of pillars , You can go to O(n) In time , Find out that all the lower boundaries are of this line 、 Is full of 1 Inside the rectangle 、 What is the largest rectangle ？ Enumerating the lower boundary of the rectangle requires O(n) Time for , So the time complexity of the whole algorithm is O(n^2)

How to preprocess each position to count up , At most how many consecutive 1 Well ？ You can pass it on

use f(i,j) Express (i,j) This grid counts up 、 At most how many consecutive 1, There are two situations

①(i,j) This grid is 0 Words , that f(i,j) Namely 0

②(i,j) This grid is not 0 Words , that f(i,j) Namely 1 +(i - 1,j) How many rectangles does this grid have up to f(i - 1,j)

class Solution {
public:
    int largestRectangleArea(vector<int>& h) {
        // Maximum length 
        int n = h.size();
        // Define the position of the first smaller number to the left of each number 、 The position of the first smaller number on the right of each number 
        vector<int> left(n),right(n);
        // Define a stack 
        stack<int> stk;
        // Scan each number from front to back 
        for(int i = 0; i < n;i ++ ) {
            // When there are elements in the stack   And the element at the top of the stack is greater than or equal to the current element   Just delete the top element of the stack 
            while(stk.size() && h[stk.top()] >= h[i]) stk.pop();
            // If the stack is empty , It means that any number is larger than the current one , The left boundary can take the leftmost side , Assign it to -1
            if(stk.empty()) left[i] = -1;
            // otherwise left[i] Equal to the subscript of the element at the top of the stack 
            else left[i] = stk.top();
            // Insert the current element into the stack 
            stk.push(i);
        }
        // Empty the stack 
        stk = stack<int>();
        // Scan each number from back to left 
        for(int i = n - 1; i >= 0; i-- ) {
            // When there are elements in the stack   And the element at the top of the stack is greater than or equal to the current element   Just delete the top element of the stack 
            while(stk.size() && h[stk.top()] >= h[i]) stk.pop();
            // If the stack is empty 
            if(stk.empty()) right[i] = n;
            // otherwise right[i] Equal to the subscript of the element at the top of the stack 
            else right[i] = stk.top();
            // Insert the current element into the stack 
            stk.push(i);
        }
        // Traverse each upper boundary   Update answers 
        int res = 0;
        for(int i = 0; i < n; i++ ) res = max(res,h[i] * (right[i] - left[i] - 1));
        return res;
    }
    int maximalRectangle(vector<vector<char>>& matrix) {
        // Empty return 0
        if(matrix.empty() || matrix[0].empty()) return 0;
        // use  n  Said height   use  m  Width 
        int n = matrix.size(),m = matrix[0].size();
        // Use a two-dimensional array h Indicates the maximum number of consecutive 1
        vector<vector<int>> h(n,vector<int>(m));
        // seek  h(i,j)
        for(int i = 0; i < n; i++) 
            for(int j = 0; j < m; j++) {
                //matrix[i][j]!='0'
                if(matrix[i][j] == '1') {
                    // If i>0  Recurrence 
                    if(i) h[i][j] = 1 + h[i - 1][j];
                    else h[i][j] = 1;
                }
            }
        int res = 0;
        // Enumerate the lower boundary 
        for(int i = 0;i < n; i++ ) res = max(res,largestRectangleArea(h[i]));
        return res;
    }
};