当前位置:网站首页>Four traversal methods of binary tree, as well as the creation of binary tree from middle order to post order, pre order to middle order, pre order to post order, and sequence [specially created for t
Four traversal methods of binary tree, as well as the creation of binary tree from middle order to post order, pre order to middle order, pre order to post order, and sequence [specially created for t
2022-07-04 20:42:00 【@Luo fan】
Blogger introduction :
– I am a 了 all WeChat official account 【 The Milky way 】 Looking forward to your attention . In the future, let's cheer together ~
Preface
The three traversal methods here need not be introduced too much , It is believed that anyone who has learned data structure can easily use recursive method to traverse , The idea of non recursive method is also consistent .
According to the previous order and the middle order 、 The middle order and the last order 、 The preface and the following preface are written with reference to the solution to the question of force deduction , Only sequence traversal is to make it inconvenient to solve problems again, so we choose to solve problems locally , But local problem solving cannot be tested , Using the other three creation methods is too cumbersome , So I want to use sequence to create binary tree , The thinking is relatively simple for your reference , Problems can be discussed in time .
List of articles
The former sequence traversal
Because it is a preorder traversal, the root node must be in front , Traversal order is ( root 、 Left 、 Right )
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// The former sequence traversal
func preorderTraversal(root *TreeNode) []int {
nums := make([]int, 0)
var dfs func(node *TreeNode)
dfs = func(node *TreeNode) {
if node != nil {
nums = append(nums, node.Val) // root
dfs(node.Left) // Left
dfs(node.Right) // Right
}
}
dfs(root)
return nums
}
In the sequence traversal
Because it is a medium order traversal, the root node must be in the middle , Traversal order is ( Left 、 root 、 Right )
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// In the sequence traversal
func inorderTraversal(root *TreeNode) []int {
nums := make([]int, 0)
var dfs func(node *TreeNode)
dfs = func(node *TreeNode) {
if node != nil {
dfs(node.Left) // Left
nums = append(nums, node.Val) // root
dfs(node.Right) // Right
}
}
dfs(root)
return nums
}
After the sequence traversal
Because it is post order traversal, the root node must be behind , Traversal order is ( Left 、 Right 、 root )
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// Subsequent traversal
func postorderTraversal(root *TreeNode) []int {
nums := make([]int, 0)
var dfs func(node *TreeNode)
dfs = func(node *TreeNode) {
if node != nil {
dfs(node.Left)
dfs(node.Right)
nums = append(nums, node.Val)
}
}
dfs(root)
return nums
}
Sequence traversal
Sequence traversal must be line by line , The idea is BFS( Like a drop of water into the pool of ripples, layer by layer ), Here, the queue is used to constantly store the next child as the next root node to traverse its child .
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// Sequence traversal
func levelOrder(root *TreeNode) [][]int {
ret := [][]int{
}
if root == nil {
return ret
}
q := []*TreeNode{
root}
for i := 0; len(q) > 0; i++ {
ret = append(ret, []int{
})
p := []*TreeNode{
}
for j := 0; j < len(q); j++ {
node := q[j]
ret[i] = append(ret[i], node.Val)
if node.Left != nil {
p = append(p, node.Left)
}
if node.Right != nil {
p = append(p, node.Right)
}
}
q = p
}
return ret
}
Sequence creation binary tree
It's the key moment , Take reference sequence traversal as the opposite thinking , First, split the one-dimensional array into nodes of each layer , Make a two-dimensional array , After that, according to traversing each child as the current root node, add its left and right children . This writing method is ugly and has low performance , Hope to buckle the bottom patiently . here -1 For null
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// Sequence creation binary tree
func sequenceCreation(nums []int) *TreeNode {
if len(nums) == 0 {
return nil
}
if len(nums) == 1 {
return &TreeNode{
nums[0], nil, nil}
}
// First, the array is divided into layers
sliNums := make([][]int, 0)
count := 1
for i := 0; i < len(nums); {
cont := make([]int, 0)
j := i
for ; j < i+count; j++ {
cont = append(cont, nums[j])
}
i = j
sliNums = append(sliNums, cont)
count *= 2
}
root := new(TreeNode)
root.Val = sliNums[0][0]
queue := []*TreeNode{
root}
count = 0
for i := 1; i < len(sliNums); i++ {
for j := 0; j < len(sliNums[i]); j += 2 {
if sliNums[i][j] != -1 {
queue[count].Left = &TreeNode{
Val: sliNums[i][j]}
queue = append(queue, queue[count].Left)
} else {
if queue[count] != nil {
queue[count].Left = nil
queue = append(queue, queue[count].Left)
}
}
if sliNums[i][j+1] != -1 {
queue[count].Right = &TreeNode{
Val: sliNums[i][j+1]}
queue = append(queue, queue[count].Right)
} else {
if queue[count] != nil {
queue[count].Right = nil
queue = append(queue, queue[count].Right)
}
}
count++
}
}
return root
}
Use cases
Here take the simple question of Li Kou as an example :104. The maximum depth of a binary tree 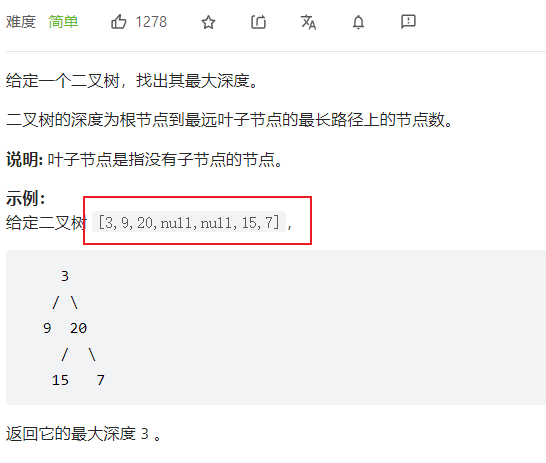
Code implementation
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func maxDepth(root *TreeNode) int {
if root == nil {
return 0
}
return max(maxDepth(root.Left), maxDepth(root.Right)) + 1
}
func main() {
nums := []int{
3, 9, 20, -1, -1, 15, 7}
root := sequenceCreation(nums) // This function is the above sequence traversal , Don't paste again here
fmt.Println(maxDepth(root))
}
test result
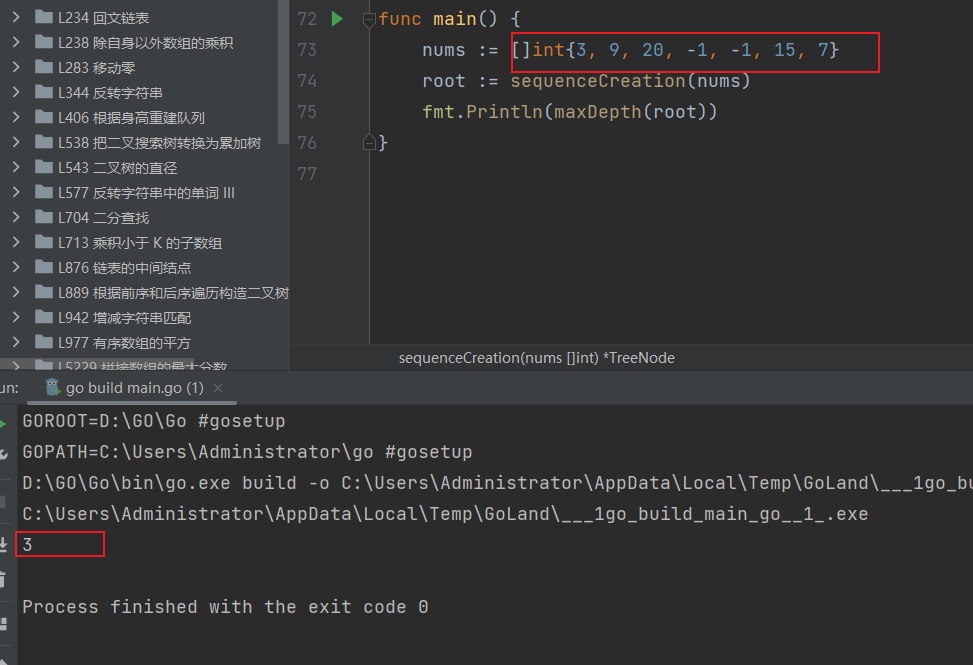
Results the correct
Create a binary tree in the previous order and the middle order
Here we refer to the solution of the problem of force deduction , Thinking is relatively simple ,preorder The beginning of the slice is the root node , And then inorder Slice and compare to find the left and right children , The creation can be completed by repeating the comparison downward .
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// Find the root node in the previous sequence , Find the left-right boundary in the middle order
func pIBuildTree(preorder []int, inorder []int) *TreeNode {
if len(preorder) == 0 {
return nil
}
root := &TreeNode{
preorder[0], nil, nil}
i := 0
for ; i < len(inorder); i++ {
if inorder[i] == preorder[0] {
break
}
}
root.Left = pIBuildTree(preorder[1:len(inorder[:i])+1], inorder[:i])
root.Right = pIBuildTree(preorder[len(inorder[:i])+1:], inorder[i+1:])
return root
}
Create a binary tree in middle order and later order
It is basically consistent with the previous order and the middle order , But this time it's the comparison between middle order and post order
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// Create a binary tree from the middle order
func iPBuildTree(inorder []int, postorder []int) *TreeNode {
idxMap := map[int]int{
}
for i, v := range inorder {
idxMap[v] = i
}
var build func(int, int) *TreeNode
build = func(inorderLeft, inorderRight int) *TreeNode {
// No remaining nodes
if inorderLeft > inorderRight {
return nil
}
// The end element of post order traversal is the root node of the current subtree
val := postorder[len(postorder)-1]
postorder = postorder[:len(postorder)-1]
root := &TreeNode{
Val: val}
// according to val The position traversed in the middle order , Divide the middle order traversal into left and right subtrees
// Because we always take the elements from the end of the post order traversal , So we should traverse the right subtree first and then the left subtree
inorderRootIndex := idxMap[val]
root.Right = build(inorderRootIndex+1, inorderRight)
root.Left = build(inorderLeft, inorderRootIndex-1)
return root
}
return build(0, len(inorder)-1)
}
Create a binary tree before and after
The result here may not be unique
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// Build a binary tree according to the previous sequence
func constructFromPrePost(preorder []int, postorder []int) *TreeNode {
// Recursion end condition
if len(preorder) == 0 {
return nil
}
// When there is only one element , Is a leaf node . This step 889 Do not omit
if len(preorder) == 1 {
return &TreeNode{
Val: preorder[0]}
}
// The root node
root := &TreeNode{
Val: preorder[0]}
// Find the position equal to the next node under the root node of the previous sequence in the subsequent sequence
for pos, node := range postorder {
if node == preorder[1] {
// Build the left subtree
root.Left = constructFromPrePost(preorder[1:pos+2], postorder[:pos+1])
// Build the right subtree
root.Right = constructFromPrePost(preorder[pos+2:], postorder[pos+1:len(postorder)-1])
break
}
}
return root
}
Reference link :
- Construct binary tree from middle order and post order traversal sequence :https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/solution/cong-zhong-xu-yu-hou-xu-bian-li-xu-lie-gou-zao-14/
- Construct binary tree according to preorder and postorder traversal :https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-postorder-traversal/solution/889-gen-ju-qian-xu-he-hou-xu-bian-li-gou-zw0i/
- Construction of binary trees from traversal sequences of preorder and middle order :https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solution/cong-qian-xu-yu-zhong-xu-bian-li-xu-lie-gou-zao-9/
It's not easy to create , Give me some advice. !
If you need to see a collection later !
If you are interested in my article, please pay attention to !
If there are questions , You can pay attention to the official account. 【 The Milky way 】 Click to contact me for private chat .
边栏推荐
- B2B mall system development of electronic components: an example of enabling enterprises to build standardized purchase, sale and inventory processes
- Flet教程之 08 AppBar工具栏基础入门(教程含源码)
- 1500万员工轻松管理,云原生数据库GaussDB让HR办公更高效
- 2022 Health Exhibition, health exhibition, Beijing Great Health Exhibition and health industry exhibition were held in November
- How does the computer save web pages to the desktop for use
- What is the application technology of neural network and Internet of things
- Aiming at the "amnesia" of deep learning, scientists proposed that based on similarity weighted interleaved learning, they can board PNAS
- Delete the characters with the least number of occurrences in the string [JS, map sorting, regular]
- LeetCode 871. Minimum refueling times
- Hash哈希竞猜游戏系统开发如何开发丨哈希竞猜游戏系统开发(多套案例)
猜你喜欢

What does the neural network Internet of things mean? Popular explanation

NetCore3.1 Json web token 中间件
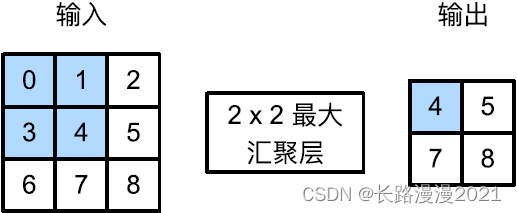
《动手学深度学习》(三) -- 卷积神经网络 CNN
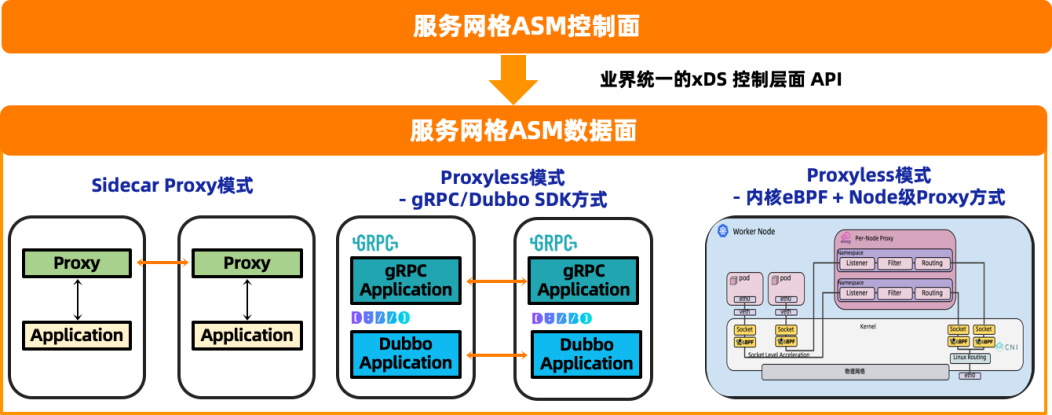
托管式服务网络:云原生时代的应用体系架构进化
Practical examples of node strong cache and negotiation cache
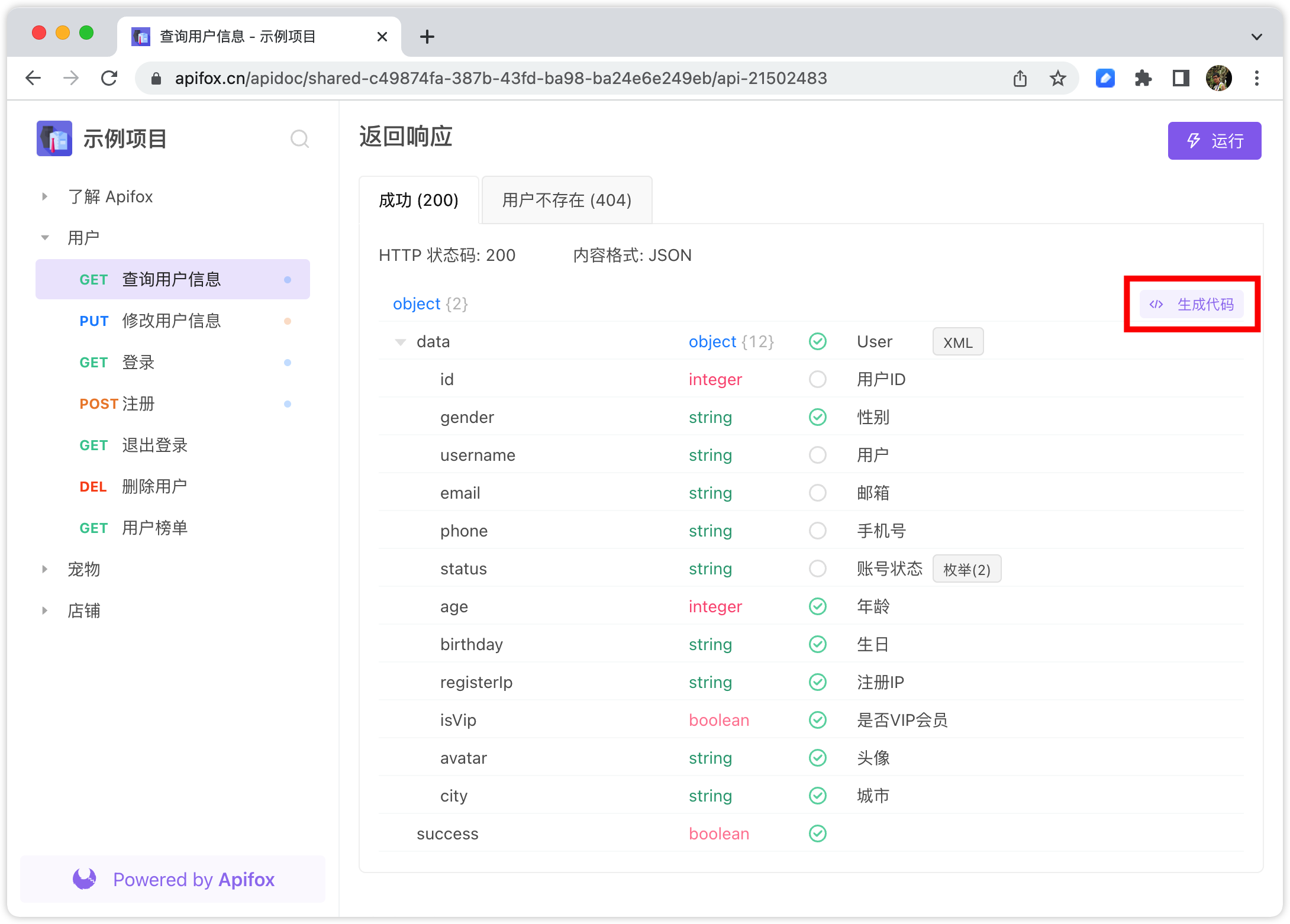
Every time I look at the interface documents of my colleagues, I get confused and have a lot of problems...

idea配置标准注释
Win11系统wifi总掉线怎么办?Win11系统wifi总掉线的解决方法
![NLP、视觉、芯片...AI重点方向发展几何?青源会展望报告发布[附下载]](/img/79/82763392e74d102921b4e8e601d4c6.png)
NLP、视觉、芯片...AI重点方向发展几何?青源会展望报告发布[附下载]
Flet教程之 05 OutlinedButton基础入门(教程含源码)
随机推荐
word中使用自动插入题注功能
什么叫内卷?
Win11亮度被锁定怎么办?Win11亮度被锁定的解决方法
Cdga | six principles that data governance has to adhere to
紫光展锐完成全球首个 5G R17 IoT NTN 卫星物联网上星实测
2022 Health Exhibition, Beijing Health Expo, China Health Exhibition, great health exhibition November 13
What if win11u disk refuses access? An effective solution to win11u disk access denial
idea插件
记一次 .NET 某工控数据采集平台 线程数 爆高分析
一文搞懂Go语言中文件的读写与创建
What if the brightness of win11 is locked? Solution to win11 brightness locking
idea配置标准注释
Hash哈希竞猜游戏系统开发如何开发丨哈希竞猜游戏系统开发(多套案例)
NLP, vision, chip What is the development direction of AI? Release of the outlook report of Qingyuan Association [download attached]
go语言笔记(2)go一些简单运用
How is the entered query SQL statement executed?
Detailed explanation of Audi EDI invoice message
tcp为啥是三次握手和四次挥手
NetCore3.1 Json web token 中间件
原来这才是 BGP 协议