当前位置:网站首页>hash 表的概念及应用
hash 表的概念及应用
2022-07-04 19:13:00 【_刘小雨】
文章目录
哈希表在算法中是不得不需要掌握的一种算法
1. hash 表的2种应用

常见用于将较大范围的数据,但是通常是离散化的,将大范围的数据映射到小范围的题型。之间讲解的区间和就是这类题型。
1.1. 拉链法
比如L取值范围是[-109 - 109] , 我们需要映射到105 范围内
通用做法是:
- 先对x mod 105 (这里的105 是随便取值的, 如果想要冲突值少, 有经验值是131 或者是13331)
- 处理冲突(因为大范围映射到小范围可能大概率会出现重复) 例子: h(11) = 3, h(23) = 3 (这里h 函数就是哈希函数)
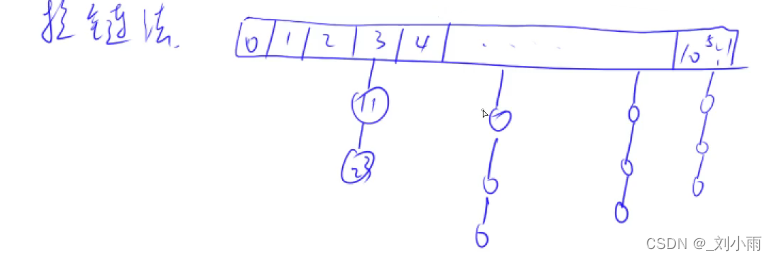
一般在哈希表中,只要实现的操作是添加和查找, 如果真需要实现删除,应该是在相应标记位上做一个标记
寻找一个大于100000 的质数
code:
#include <iostream>
using namespace std;
int main()
{
for(int i = 100000;; i ++)
{
bool flag = true;
for(int j = 2; j * j <= i; j ++)
if(i % j == 0)
{
flag = false;
break;
}
if (flag)
{
cout << i << endl;
break;
}
}
return 0;
}
1.2. 开放寻址法
另外的开放寻址法在这篇文章中有介绍:
https://blog.csdn.net/qq_39486027/article/details/125096272
开放寻址法:一般开数组是原先小范围的2-3倍
添加:
- 经过h(x) 得出应该存在哪一个位置;
- 看该位置是否有人,如果有人继续往下,直到没有人,保存;如果没人,直接保存。
查找:
- 直接查找指定的位置,如果有元素,比较是不是查找的值, 不等于,看下一个位置是不是,依次类推,直到找到或者下一次没有元素
删除:
- 先查找,如果找到后,做一个标记
下面有个相关模拟hash 得例题:
2. hash 表的相关例题
题目:
维护一个集合,支持如下几种操作:
I x,插入一个数 x;
Q x,询问数 x 是否在集合中出现过;
现在要进行 N 次操作,对于每个询问操作输出对应的结果。
输入格式
第一行包含整数 N,表示操作数量。
接下来 N 行,每行包含一个操作指令,操作指令为 I x,Q x 中的一种。
输出格式
对于每个询问指令 Q x,输出一个询问结果,如果 x 在集合中出现过,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤N≤105
−109≤x≤109
输入样例:
5
I 1
I 2
I 3
Q 2
Q 5
输出样例:
Yes
No
2.1 拉链法代码实现:
Code:
#include <iostream>
#include <cstring>
using namespace std;
const int N = 100003;
int h[N], e[N], ne[N], idx;
/// 拉链法
void insert(int x)
{
int k = (x % N + N) % N;
e[idx] = x; // 单链表的插入
ne[idx] = h[k];
h[k] = idx ++;
}
bool find(int x)
{
int k = (x % N + N ) % N;
for(int i=h[k]; i != -1; i= ne[i])
if(e[i] == x)
return true;
return false;
}
int main()
{
int n;
cin >> n;
memset(h, -1, sizeof h);
while(n --)
{
char op[2];
int x;
cin >> op >> x;
if(op[0] =='I') insert(x);
else
{
if(find(x)) puts("Yes");
else puts("No");
}
}
return 0;
}
2.2 开放寻址法代码实现:
Code:
#include <iostream>
#include <cstring>
using namespace std;
const int N = 200003, null = 0x3f3f3f3f;
int h[N];
// 开放寻址法
// 返回的x : 存在的话, 返回x的位置
// 不存在的话, 返回的是应该存储的位置
int find(int x)
{
int k = (x % N + N) % N;
while(h[k] != null && h[k] != x)
{
k++;
if(k == N) k = 0;
}
return k;
}
int main()
{
int n;
cin >> n;
memset(h, 0x3f, sizeof h);
while(n --)
{
char op[2];
int x;
cin >> op >> x;
if(op[0] =='I')
{
int k = find(x);
h[k] = x;
}
else
{
int k = find(x);
if(h[k] != null) puts("Yes");
else puts("No");
}
}
return 0;
}
3. 字符串hash 方式
另外一个是字符串hash。
3.1 字符串hash 处理原理
这里是讲字符串前缀哈希
例如: str = “ABCDEFG”
我们利用hash 函数需要求出字符串前缀哈希,什么是字符串前缀哈希呢
h[0] = 0
h[1] = “A” 的hash 值
h[2] = “AB” 的hash 值
h[3] = “ABC” 的hash 值
…
那么我们如何定义这个前缀hash值,这里用得步骤方法时这样的
例如: str = “ABCD”
第一步: 将上面的字符 映射成从1开始的 A - 1; B - 2 …
第二步: 将上面的字符串看成是一个P进制的数 (1234)p 。 这里的P 是一个经验值 : 131 或者是13331.
第三步: 然后将上面的P进制的数转换成 十进制的数字。 然后mod 一个数字264. 为了保证不冲突。
(1 * P3 + 2 * P2 + 3 * P 1 + 4 * P 0) mod (264).
这里映射成hash值是保证不冲突的,所以在这里不用考虑冲突处理的方式。
【注意】:
- 不能将字符映射成0
2.假定人品足够好, 不存在冲突, 一般来说, p 取 131、13331 是 ;q取 264 时, 几乎不存在冲突。
3.2 字符串哈希 计算推导
有了上面计算前缀字符串hash 值,我们可以计算每段每段字符串的hash 值,怎么做呢
举个例子: 加入需要求L-R 这一段的hash 值。
因为已知的是前缀hash 值,h[R] 、h[L - 1] 都知道。
我们这里是将这段字符看成P 进制的数, 因此左边是高位,右边是低位。
计算公式在图中已经给出
在一些题目中,是只能用字符串哈希处理的,用kmp 都没这个方法好,所以一定他要知道
3.3 字符串哈希应用例题
下面有一个相关得例题
题目:
给定一个长度为n的字符串,再给定m个询问,每个询问包含四个整数l1,r1,l2,r2,请你判断[l1,r1]和[l2,r2]这两个区间所包含的字符串子串是否完全相同。
字符串中只包含大小写英文字母和数字。
输入格式
第一行包含整数n和m,表示字符串长度和询问次数。
第二行包含一个长度为n的字符串,字符串中只包含大小写英文字母和数字。
接下来m行,每行包含四个整数l1,r1,l2,r2,表示一次询问所涉及的两个区间。
注意,字符串的位置从1开始编号。
输出格式
对于每个询问输出一个结果,如果两个字符串子串完全相同则输出“Yes”,否则输出“No”。
每个结果占一行。
数据范围
1≤n,m≤105
输入样例:
8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2
输出样例:
Yes
No
Yes
3.4 字符串哈希代码实现
Code:
#include <iostream>
using namespace std;
typedef unsigned long long ULL;
const int N = 100010, P = 131; // 这里的P 是经验值 131 ,或者13331
int n,m;
char str[N];
// 这里用unsigned long long 存储就相当于mod 2 ^ 64, 因为超过了会溢出的
ULL h[N], p[N]; // h[]是存储字符串哈希值的 p[] 是存储p次方的
ULL get(int l, int r)
{
return h[r] - h[l -1] * p[r - l + 1]; // 区间hash 的公式
}
int main()
{
scanf("%d%d%s", &n, &m, str + 1);
p[0] = 1;
for(int i=1; i<=n; i++)
{
p[i] = p[i-1] * P; // p数组保存 计算的次方数
h[i] = h[i-1] * P +str[i]; // 计算字符串的前缀, 后面的是0次 所以直接加上str[i]就行了
}
while(m -- )
{
int l1, r1, l2, r2;
scanf("%d%d%d%d", &l1, &r1, &l2, &r2);
if(get(l1, r1) == get(l2, r2)) cout << "Yes" << endl;
else cout << "No" << endl;
}
return 0;
}
推荐一个零声学院免费公开课程,个人觉得老师讲得不错,分享给大家:Linux,Nginx,ZeroMQ,MySQL,Redis,fastdfs,MongoDB,ZK,流媒体,CDN,P2P,K8S,Docker,TCP/IP,协程,DPDK等技术内容,立即学习
边栏推荐
- Fleet tutorial 08 introduction to AppBar toolbar Basics (tutorial includes source code)
- Implementation of redis distributed lock
- Flet教程之 08 AppBar工具栏基础入门(教程含源码)
- What is the development of block hash quiz game system? Hash quiz game system development (case mature)
- Advantages of semantic tags and block level inline elements
- 工厂从自动化到数字孪生,图扑能干什么?
- 科普达人丨一文看懂阿里云的秘密武器“神龙架构”
- 电脑页面不能全屏怎么办?Win11页面不能全屏的解决方法
- 【深度学习】一文看尽Pytorch之十九种损失函数
- idea插件
猜你喜欢
How does win11 search for wireless displays? Win11 method of finding wireless display device
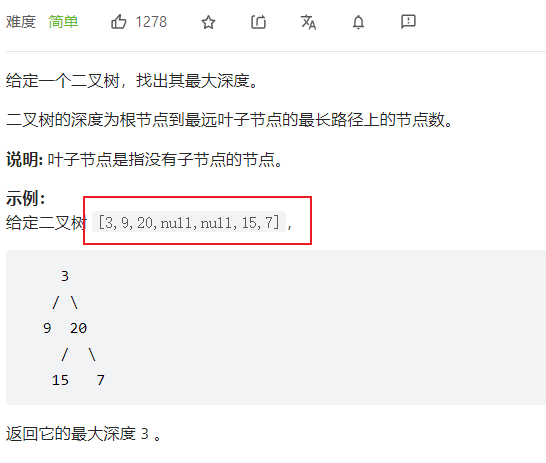
二叉树的四种遍历方式以及中序后序、前序中序、前序后序、层序创建二叉树【专为力扣刷题而打造】

From automation to digital twins, what can Tupo do?

九齐NY8B062D MCU规格书/datasheet

Ziguang zhanrui completed the first 5g R17 IOT NTN satellite on the Internet of things in the world
Flet教程之 08 AppBar工具栏基础入门(教程含源码)
B2B mall system development of electronic components: an example of enabling enterprises to build standardized purchase, sale and inventory processes
Flet tutorial 06 basic introduction to textbutton (tutorial includes source code)
How does the computer save web pages to the desktop for use
Form组件常用校验规则-1(持续更新中~)
随机推荐
Understand Alibaba cloud's secret weapon "dragon architecture" in the article "science popularization talent"
Function analysis and source code of hash guessing game system development
FS4061A升压8.4V充电IC芯片和FS4061B升压12.6V充电IC芯片规格书datasheet
Redis分布式锁的实现
复杂因子计算优化案例:深度不平衡、买卖压力指标、波动率计算
九齐NY8B062D MCU规格书/datasheet
长城证券开户安全吗 股票开户流程网上开户
Stack: how to realize the judgment of valid brackets?
Practical examples of node strong cache and negotiation cache
mysql语句执行详解
What if the computer page cannot be full screen? The solution of win11 page cannot be full screen
jekins初始化密码没有或找不到
QT writing the Internet of things management platform 38- multiple database support
被奉为经典的「金字塔原理」,教给我们哪些PPT写作技巧?
What if win11u disk refuses access? An effective solution to win11u disk access denial
Hash哈希竞猜游戏系统开发如何开发丨哈希竞猜游戏系统开发(多套案例)
Six stones programming: about code, there are six triumphs
Lingyun going to sea | Wenhua online & Huawei cloud: creating a new solution for smart teaching in Africa
如何让你的小游戏适配不同尺寸的手机屏幕
面对同样复杂的测试任务为什么大老很快能梳理解决方案,阿里十年测试工程师道出其中的技巧