当前位置:网站首页>AtCoder Beginner Contest 261 部分题解
AtCoder Beginner Contest 261 部分题解
2022-07-31 02:03:00 【山中一扶苏】
本篇题解只是记录我的做题过程代码,不提供最优解
(另外这里所有的时间复杂度都只分析单个样例,不算 t t t的时间复杂度)
A
点击此处查看对应的题目.
本题设计算法:差分
给出两个区间,利用差分直接算出重合区间即可
时间复杂度 O ( m a x ( b , d ) ) O(max(b,d)) O(max(b,d))
#include <iostream>
#include <cstring>
#include <algorithm>
#include <set>
#include <vector>
using namespace std;
typedef pair<int,int> PII;
typedef long long ll;
const ll N = 2e5 + 10,mod = 1e9 + 7;
int s[N];
int main()
{
int a,b,c,d;
cin >> a >> b >> c >> d;
s[a] ++,s[b] --;s[c] ++,s[d] --;
int maxn = max(b,d),res = 0;
for (int i = 1;i <= maxn;i ++ ) s[i] += s[i - 1];
for (int i = 0;i <= maxn;i ++ )
if (s[i] == 2) res ++;
cout << res << '\n';
return 0;
}
B
点击此处查看对应的题目.
本题设计算法:模拟
直接模拟题意,是否满足对角线即可。
时间复杂度 O ( n 2 ) O(n ^ 2) O(n2)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <set>
#include <vector>
using namespace std;
typedef pair<int,int> PII;
typedef long long ll;
const ll N = 2010;
char g[N][N];
int main()
{
int n;
cin >> n;
for (int i = 0;i < n;i ++ ) {
string s;
cin >> s;
for (int j = 0;j < n;j ++ ) {
g[i][j] = s[j];
}
}
for (int i = 0;i < n;i ++ ) {
for (int j = 0;j < n;j ++ ) {
if ((g[i][j] == 'W' && g[j][i] != 'L') || (g[i][j] == 'L' && g[j][i] != 'W') || (g[i][j] == 'D' && g[j][i] != 'D')) {
cout << "incorrect" << '\n';
return 0;
}
}
}
cout << "correct" << '\n';
return 0;
}
C
点击此处查看对应的题目.
本题设计算法:map统计
直接利用map统计字符串出现的次数即可
时间复杂度 O ( n ) O(n) O(n)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <vector>
using namespace std;
typedef pair<int,int> PII;
typedef long long ll;
const ll N = 2e5 + 10;
string s[N];
int main()
{
int n;
cin >> n;
unordered_map<string,int> mp;
for (int i = 0;i < n;i ++ ) cin >> s[i];
for (int i = 0;i < n;i ++ ) {
if (mp.count(s[i]) == 0) cout << s[i] << '\n';
else {
cout << s[i] << "(" << mp[s[i]] << ")" << '\n';
}
mp[s[i]] ++;
}
return 0;
}
D
点击此处查看对应的题目.
本题设计算法:动态规划的背包问题
本题由题意可以看出每次投掷硬币就是两种可能性。
- 1是正面朝上
- 2 是反面朝上
最后通过枚举n次投掷,计数器的各种情况,值得一提的是,在第 i 次投掷中计数器的计数情况最多为 i,因为每次最多就是加一或是清零。
状态表示与状态转移在以下代码中注释出来了,详细见以下代码
时间复杂度 O ( n 2 ) O(n^2) O(n2)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <vector>
using namespace std;
typedef pair<int,int> PII;
typedef long long ll;
const ll N = 5010,INF = 1e18;
ll dp[N][N];//前i次投硬币中,当前计数器为j的最大收益
ll val[N];
int main()
{
int n,m;
cin >> n >> m;
ll maxc = 0;
unordered_map<ll,ll> mp;
for (int i = 1;i <= n;i ++ ) cin >> val[i];
for (int i = 1;i <= m;i ++ ) {
int a,b;
cin >> a >> b;
mp[a] = b;
}
for (int i = 1;i <= n;i ++ ) {
for (int j = 1;j <= i;j ++ ) {//枚举正面朝上的情况
dp[i][j] = dp[i - 1][j - 1] + val[i] + mp[j];
}
for (int j = 0;j <= i;j ++ ) {//枚举有反面朝上的情况
dp[i][0] = max(dp[i][0],dp[i - 1][j]);
}
}
ll res = 0;
for (int i = 0;i <= n;i ++ ) res = max(res,dp[n][i]);
cout << res << '\n';
return 0;
}
E
点击此处查看对应的题目.
本题设计算法:位运算
我们考虑拆位,对于第 i 位算出来最终是 0 还是 1。现在只需要考虑 X , A i ∈ 0 , 1 X,A_i∈ {0,1} X,Ai∈0,1 的情形。
可以发现,这些操作虽然不具有结合律,但最终操作带来的贡献可以等效为以下四种:
- 将原数保持不变。
- 将原数取反。
- 将原数强制赋值为 0。(即 x←x and 0 )
- 将原数强制赋值为 1。(即 x←x or 1 )
其他的情况都不会给 X 带来变化和贡献。
xor 的贡献相当于将目前的贡献在第 3,4 种之间互换,或者在第 1,2 种之间互换。
于是我们就处理出了操作序列的每个前缀等效的贡献。最后把每一位合并起来就行了。
时间复杂度 O ( n l o g a ) O(nloga) O(nloga)
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#include <vector>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const ll N = 2e5 + 10,INF = 1e18;
int t[N],a[N],res[N],ans[N];
int main()
{
int n,x;
cin >> n >> x;
for (int i = 1;i <= n;i ++ ) cin >> t[i] >> a[i];
for (int i = 0;i < 30;i ++ ) {
int val = x >> i & 1,now = 0;
for (int j = 1;j <= n;j ++ ) {//真正会变的只有这三种情况
int k = a[j] >> i & 1;
if (k == 0 && t[j] == 1) now = 1;
else if (k == 1 && t[j] == 2) now = 2;
else if (k == 1 && t[j] == 3) now = 3 - now;
res[j] = now;
}
for (int j = 1;j <= n;j ++ ) {
if (res[j] == 1) val = 0;
else if (res[j] == 2) val = 1;
else if (res[j] == 3) val = val ^ 1;
ans[j] = (ans[j] | (val << i));
}
}
for (int i = 1;i <= n;i ++ ) cout << ans[i] << '\n';
return 0;
}
边栏推荐
- mysql index
- uniapp使用第三方字体
- Crypto Life, a day in the life of a Web3 project partner
- Drools WorkBench的简介与使用
- ShardingJDBC usage summary
- Nacos
- [1154]如何将字符串转换为datetime
- VSCode插件:嵌套注释
- Software testing basic interface testing - getting started with Jmeter, you should pay attention to these things
- Project development software directory structure specification
猜你喜欢
The final exam first year course
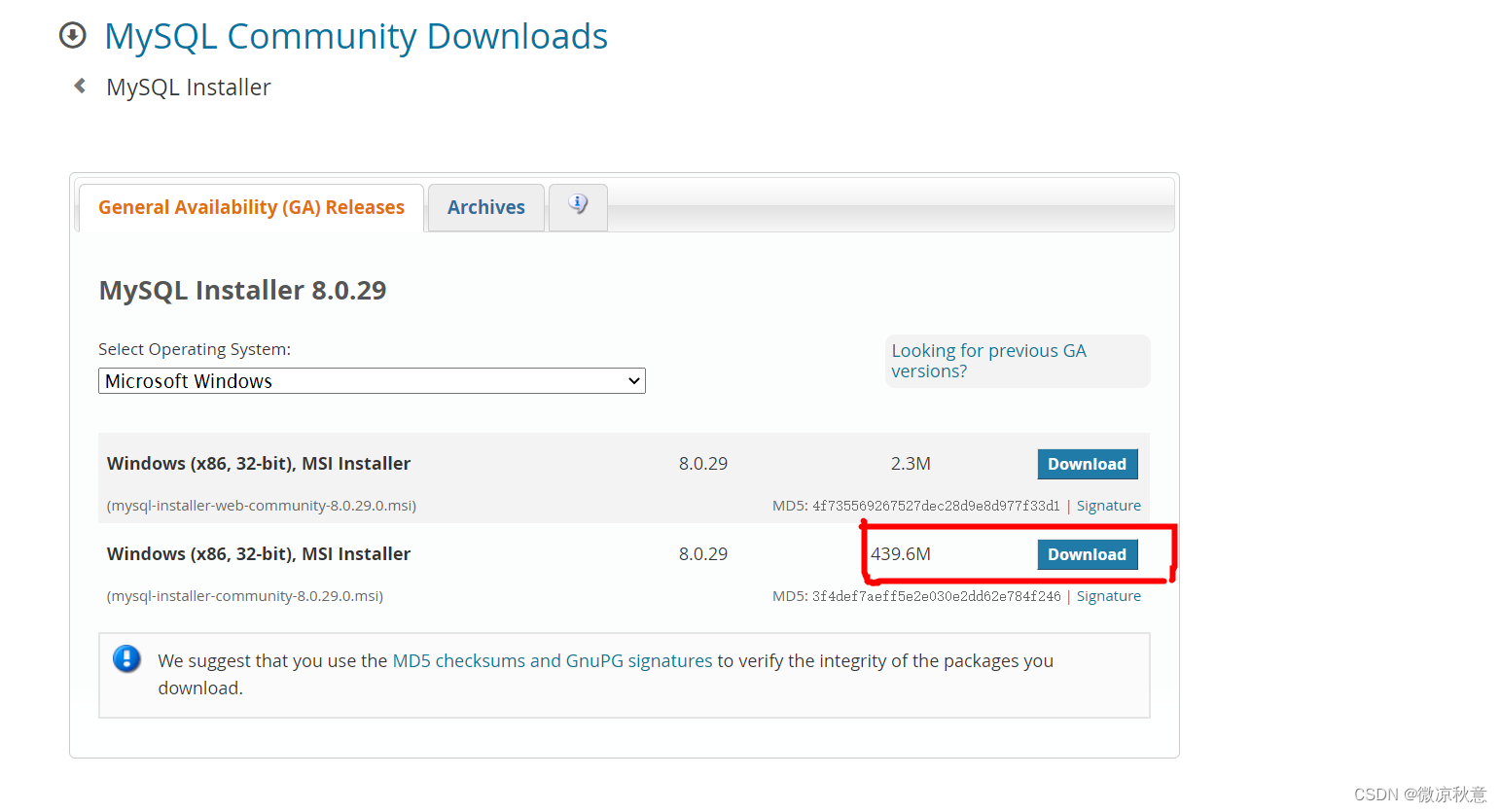
MySql installation and configuration super detailed tutorial and simple method of building database and table

ShardingJDBC usage summary

二层广播风暴(产生原因+判断+解决)
![The comprehensive result of the case statement, do you know it?[Verilog Advanced Tutorial]](/img/8a/28427aa773e46740eda9e95f6669f2.png)
The comprehensive result of the case statement, do you know it?[Verilog Advanced Tutorial]

加密生活,Web3 项目合伙人的一天
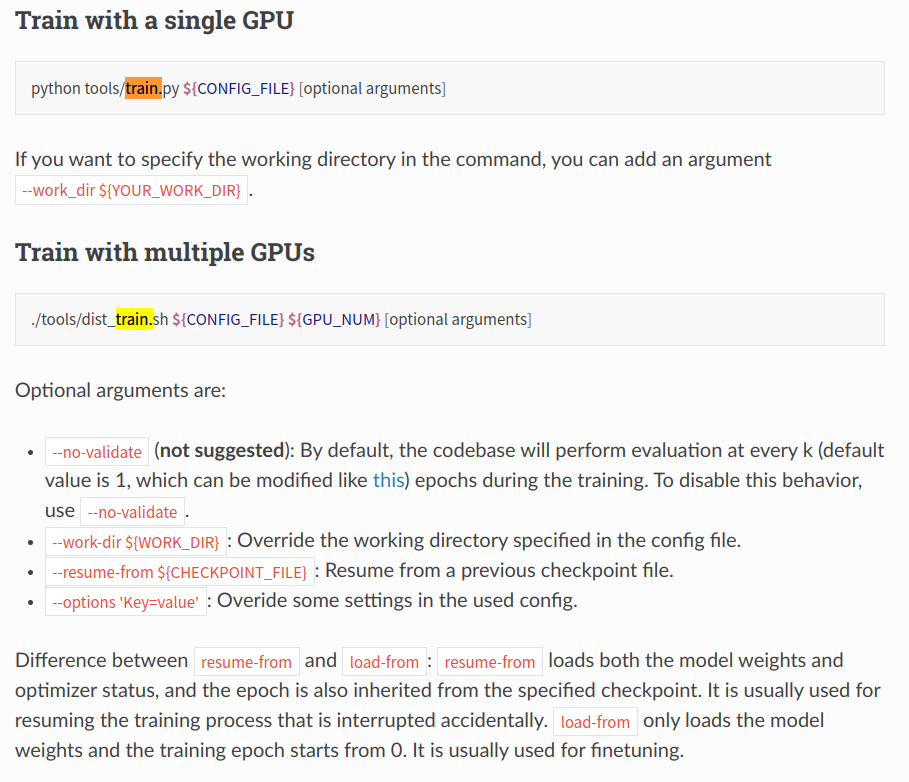
mmdetection trains a model related command
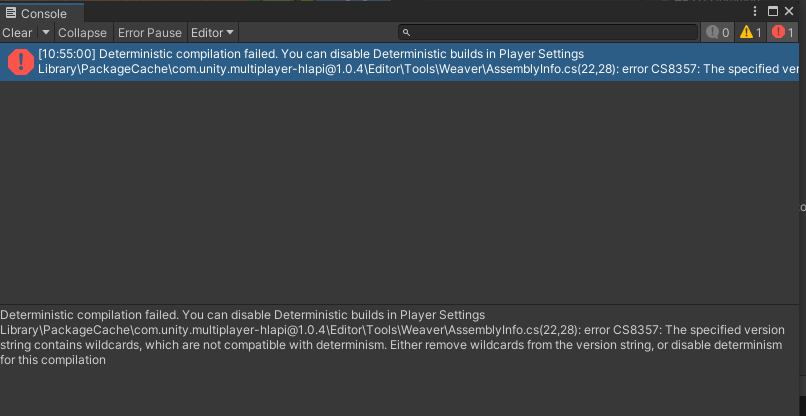
multiplayer-hlap 包有问题,无法升级的解决方案
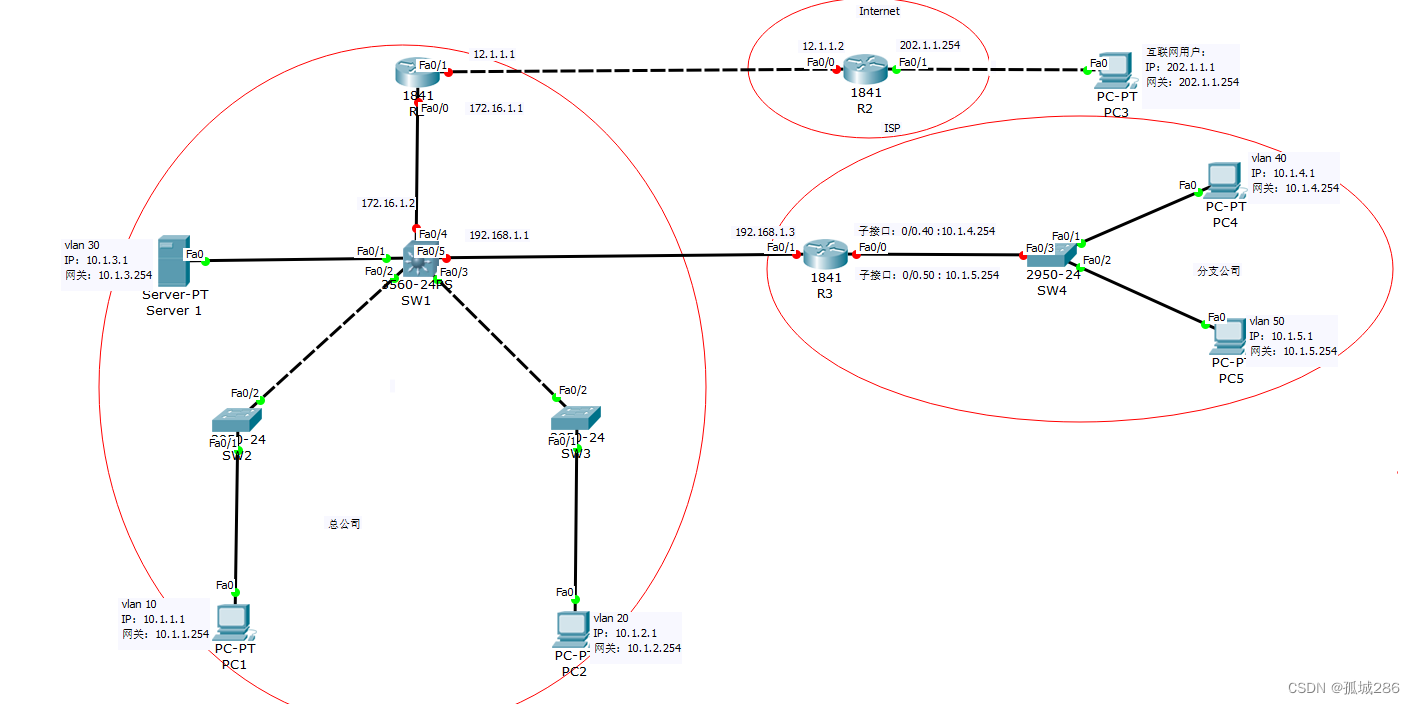
Inter-vlan routing + static routing + NAT (PAT + static NAT) comprehensive experiment
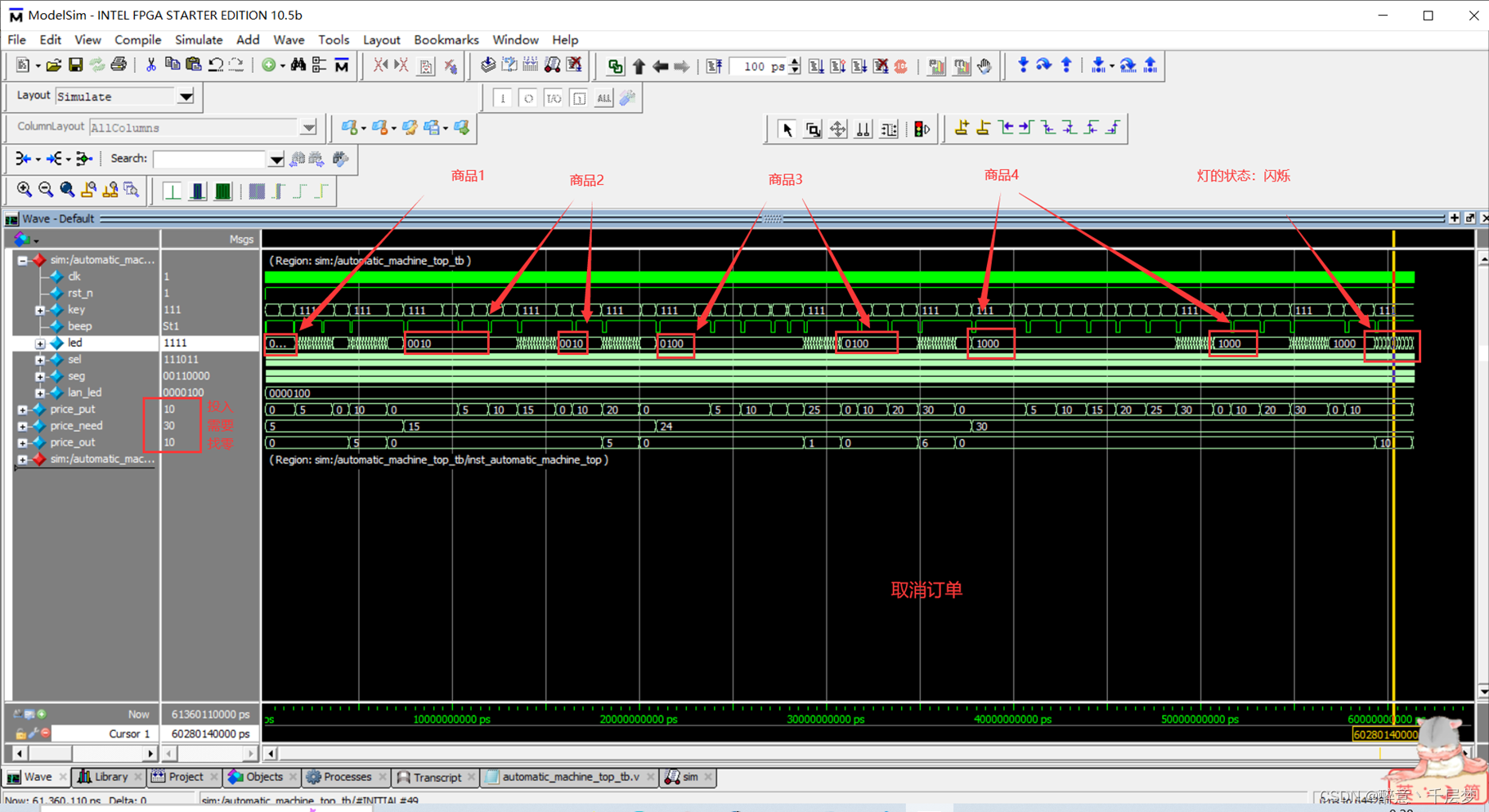
FPGA-based vending machine
随机推荐
The PC side determines the type of browser currently in use
Real-time image acquisition based on FPGA
Software Testing Defect Reporting - Definition, Composition, Defect Lifecycle, Defect Tracking Post-Production Process, Defect Tracking Process, Purpose of Defect Tracking, Defect Management Tools
Charging effect simulation
最大路径和
pycharm cannot run after renaming (error: can't open file...No such file or directory)
两个有序数组间相加和的Topk问题
Path and the largest
Drools basic introduction, introductory case, basic syntax
Fiddler抓包模拟弱网络环境测试
[1154] How to convert string to datetime
934. 最短的桥
[Map and Set] LeetCode & Niu Ke exercise
Is there a way to earn 300 yuan a day by doing a side business?
leetcode-128: longest continuous sequence
静态路由解析(最长掩码匹配原则+主备路由)
Arbitrum Interview | L2 Summer, what does the standout Arbitrum bring to developers?
【微信小程序】一文带你了解数据绑定、事件绑定以及事件传参、数据同步
Interprocess communication study notes
Nacos