当前位置:网站首页>Tenthousand words thoroughly learn heap and binary tree
Tenthousand words thoroughly learn heap and binary tree
2022-06-11 09:43:00 【Life is made by oneself ~】
Heaps and binary trees
- Pile up
- Binary tree
- One 、 Four traversal sequences
- Two 、 Binary tree interface implementation
- 3、 ... and 、 Depth first breadth first traversal ️️
Pile up
One 、 The basic concept of heap
Pile up (heap) Is a general term for a special class of data structures in computer science . The heap is usually an array object that can be thought of as a tree .
Two properties :
1️⃣ The value of a node in the heap is always not greater than or less than the value of its parent node ;
2️⃣ The heap is always a complete binary tree .
So the pile is either a big pile or a small pile
1.1 Perfect binary tree
The depth of a tree is one k There are n A binary tree of nodes , Click from top to bottom for the nodes in the tree 、 Number from left to right , If the number is i(1≤i≤n) The node and the full binary tree are numbered as i The nodes of the binary tree have the same position , This binary tree is called a complete binary tree .
Two 、 Piles and small piles
According to the two properties of heap, it can be divided into A lot and Little heap
A lot ( A father is bigger than a child ):
Little heap ( A father is smaller than a child ):
3、 ... and 、 Heap formula
Suppose the father's subscript is parent
leftchild = 2 * parent + 1;
rightchild = leftchild + 1;
Suppose the child's subscript is child( Left or right )
parent = (child - 1) / 2.
Four 、 Adjust the algorithm down
Now we're going to make the pile smaller 
Prerequisite : Both the left subtree and the right subtree are small piles , And the whole tree is not a pile
Use diagrams to illustrate the process :
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
// Downward adjustments
// Little heap
void AdjustDown(int a[], int n, int parent)
{
int child = 2 * parent + 1;
while (child < n)
{
if (child + 1 < n && a[child] > a[child + 1])
{
child++;
}
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
int main()
{
int a[] = {
27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };
int sz = sizeof(a) / sizeof(a[0]);
AdjustDown(a, sz, 0);
return 0;
}
If you want to build a lot , Just reverse the two greater than less than signs
5、 ... and 、 Building the heap
The downward adjustment algorithm above must satisfy that both the left subtree and the right subtree are small heaps , But if If this condition is not met, the reactor needs to be built 
As shown in the figure, the right subtree does not satisfy the small heap
Build the heap from the bottom up :
From the penultimate non leaf node (28), From back to front , Adjust downward in turn .
The time complexity of reactor construction is O(N)
28 Find the method at the node (n A digital ):
(n - 1 - 1)/ 2
// Building the heap
for (int i = (sz - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, sz, i);
}
6、 ... and 、 Heap sort ( Fallible )️️
In ascending order to build a lot of , Build small piles in descending order
If the reverse is true, the time complexity is O(N^2), And the relationship between father and son is in a mess
Think in descending order :
Select the small one and put it behind the array , Choose the smaller one in turn
Method :
Build a small pile , Swap closing elements , Don't treat the tail elements as those in the heap , Then adjust down ( The others are small piles ), You can choose the next smaller one ……
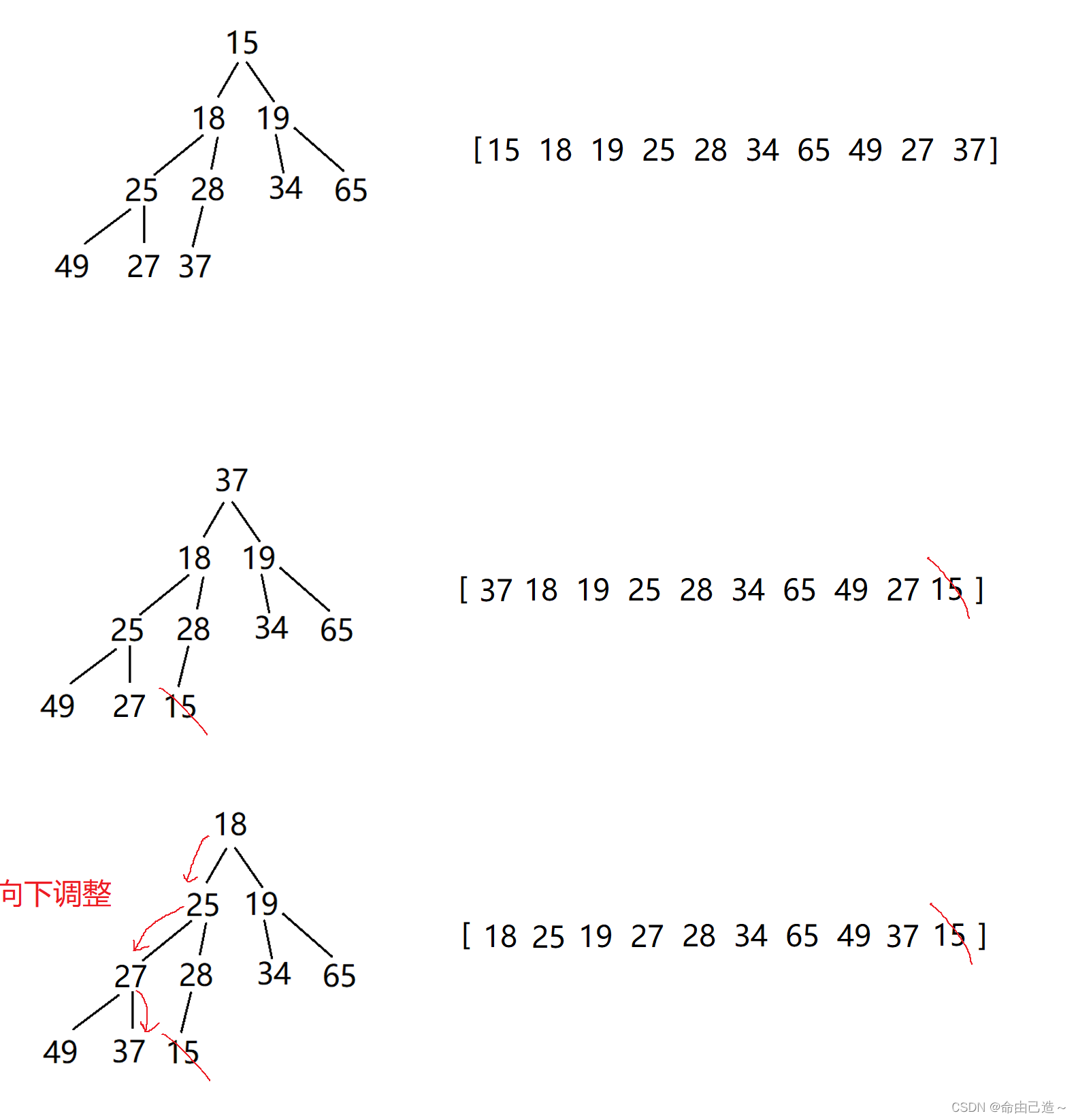
Move the array elements forward in turn , After adjustment, there are small piles .
such The time complexity is O(N * logN),( Building the heap * Downward adjustments )
void HeapSort(int a[], int n)
{
// Build a small pile ( Descending )
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
int end = n - 1;
while (end)
{
Swap(&a[0], a[end]);
AdjustDown(a, end, 0);
end--;
}
}
7、 ... and 、 Interface implementation of heap
Interface preview :

The structure of the pile
typedef int HPDataType;
struct Heap
{
HPDataType* a;
int size;
int capacity;
};
typedef struct Heap HP;
7.1 Initialization of the heap
void HeapInit(HP* php, HPDataType* a, int n)
{
assert(php);
php->a = (HPDataType*)malloc(sizeof(HPDataType) * n);
if (php->a == NULL)
{
printf("malloc fail\n");
exit(-1);
}
memcpy(php->a, a, n * sizeof(HPDataType));
php->size = php->capacity = n;
// Building the heap
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(php->a, php->size, i);
}
}
7.2 Heap destruction
void HeapDestroy(HP* php)
{
assert(php);
free(php->a);
php->a = NULL;
php->size = 0;
php->capacity = 0;
}
7.3 Pile insertion
When inserting, pay attention to judge whether it is full
void HeapPush(HP* php, HPDataType x)
{
assert(php);
if (php->size == php->capacity)
{
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity * 2);
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
php->a = tmp;
php->capacity *= 2;
}
php->a[php->size] = x;
php->size++;
// Adjust up
AdjustUp(php->a, php->size - 1);
}
After insertion, it should be adjusted to a small heap ( Or a lot of them ), Take the upward adjustment algorithm
void AdjustUp(int* a, int child)
{
int parent = (child - 1) / 2;
while (child)
{
if (a[parent] > a[child])
{
Swap(&a[parent], &a[child]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
7.4 Heap delete
To delete, first swap the first and last elements , Delete tail , Then adjust the first element downward
void HeapPop(HP* php)
{
assert(php);
assert(php->size > 0);
Swap(&php->a[0], &php->a[php->size - 1]);
php->size--;
AdjustDown(php->a, php->size, 0);
}
7.5 Return to the top of heap element
HPDataType HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);
return php->a[0];
}
7.6 The size of the heap
int HeapSize(HP* php)
{
assert(php);
return php->size;
}
7.7 Determine whether it is null
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
7.8 Print heap
Print heap with conditional control shape
void HeapPrint(HP* php)
{
assert(php);
int row = 0;
for (row = 1; row < php->size; row++)
{
if ((int)(pow(2, row) - 1) / php->size != 0)
{
break;
}
}
int col = (int)pow(2, row - 1);
int i = 0;
int k = 0;
for (i = 0; i < row; i++)
{
int j = 0;
// Print space
for (j = 0; j < (col / 2) - i - 1; j++)
{
printf(" ");
}
for (j = 0; j < (int)pow(2, i); j++)
{
if (k >= php->size)
{
break;
}
printf("%d ", php->a[k++]);
}
printf("\n");
}
}
design sketch :
8、 ... and 、TopK problem ️️

Directly build a heap and sort the heap , however If there is a lot of data , will malloc Very many nodes , There will be problems .
So we can just choose the front k Build a lot of numbers , Compare all the numbers in the back , If the number of elements at the top of the heap is greater than the number at the back , Let the top of the heap be this number , Then adjust it down to a lot of . The last heap is the smallest k Number
/** * Note: The returned array must be malloced, assume caller calls free(). */
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
// A lot
void AdjustDown(int* a, int n, int parent)
{
int child = 2 * parent + 1;
while(child < n)
{
if(child + 1 < n && a[child] < a[child + 1])
{
child++;
}
if(a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
int* getLeastNumbers(int* arr, int arrSize, int k, int* returnSize){
if(k == 0)
{
*returnSize = 0;
return NULL;
}
// Before fetching k Number
int* a = (int*)malloc(sizeof(int) * k);
for(int i = 0; i < k; i++)
{
a[i] = arr[i];
}
// Build a pile
for(int i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, k, i);
}
for(int i = k; i < arrSize; i++)
{
if(a[0] > arr[i])
{
a[0] = arr[i];
AdjustDown(a, k, 0);
}
}
*returnSize = k;
return a;
}
Binary tree
One 、 Four traversal sequences
1.1 The former sequence traversal
root → Left → Right
A→B→C→NULL→NULL→D→NULL→NULL→E→NULL→F→NULL→NULL
1.2 In the sequence traversal
Left → root → Right
NULL→C→NULL→B→NULL→D→NULL→A→NULL→E→NULL→F→NULL
1.3 After the sequence traversal
Left → Right → root
NULL→NULL→C→NULL→NULL→D→B→NULL→NULL→NULL→F→E→A
1.4 Sequence traversal
Go one floor at a time
A→B→E→C→D→F
Two 、 Binary tree interface implementation
2.1 The former sequence traversal
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%c ", root->val);
PreOrder(root->left);
PreOrder(root->right);
}
2.2 In the sequence traversal
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%c ", root->val);
InOrder(root->right);
}
2.3 After the sequence traversal
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%c ", root->val);
}
2.4 Find the number of nodes
int TreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
2.5 Find the number of leaf nodes
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
2.6 Please K Layer nodes ️️
Find the... Of the current tree K The nodes of the layer can be regarded as the solution ( From the second floor ) The first K-1 The number of nodes in the layer …… seek ( From K Layer view ) The first 1 The number of layer nodes
int TreeLevelSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return TreeLevelSize(root->left, k - 1) + TreeLevelSize(root->right, k - 1);
}
2.7 Find the target node ️️
BTNode* TreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->val == x)
{
return root;
}
BTNode* left = TreeFind(root->left, x);
if (left)
{
return left;
}
BTNode* right = TreeFind(root->right, x);
if (right)
{
return right;
}
return NULL;
}
2.8 Destruction of binary tree ️️
Post order traversal destroys nodes : First destroy the left tree, then the right tree, and then destroy yourself
2.8.1 First level pointer
void TreeDestroy(BTNode* root)
{
if (root == NULL)
{
return;
}
TreeDestroy(root->left);
TreeDestroy(root->right);
free(root);
}
A = NULL;
If you use the first level pointer, you should set the pointer to null after calling the destroy function .
2.8.2 The secondary pointer
void TreeDestroy(BTNode** pproot)
{
if (*pproot == NULL)
{
return;
}
TreeDestroy(&(*pproot)->left);
TreeDestroy(&(*pproot)->right);
free(*pproot);
*pproot = NULL;
}
3、 ... and 、 Depth first breadth first traversal ️️
3.1 Depth-first traversal
It starts with an unreachable vertex in the graph , Go all the way to the end , Then back from the node at the end of the road to the previous node , Start from another road to the end …, Repeat this process recursively , Until all the vertices are traversed , It is characterized by not hitting the south wall and not looking back , Go one way first , Another way to go .
The first, middle and last order traversal of binary tree is depth first traversal
3.2 Breadth first traversal
Breadth first traversal , It refers to starting from an unretraversal node of the graph , First, traverse the adjacent nodes of this node , Then traverse the adjacent nodes of each adjacent node in turn .
Sequence traversal of binary tree is breadth first traversal
3.3 Implementation of sequence traversal
First, determine to implement with queue
1. Put the root in the queue first

2. Out of line header data , Bring in the next layer of data

First introduce the written queue : Tenthousand words thoroughly learn stack and queue
void TreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%c ", front->data);
if (front->left)
{
QueuePush(&q, front->left);
}
if (front->right)
{
QueuePush(&q, front->right);
}
}
QueueDestroy(&q);
}
3.4 Determine whether it is a complete binary tree
Use two binary trees to summarize the rules :
It can be seen that complete binary tree sequence traversal only occurs NULL, The back ones are NULL;
Not a complete binary tree NULL There will be something wrong behind NULL The node of
bool BinaryTreeComplete(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
{
QueuePush(&q, root);
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
{
break;
}
else
{
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
}
while (!QueueEmpty(&q))
{
BTNode* cur = QueueFront(&q);
QueuePop(&q);
if (cur)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}
边栏推荐
- go连接数据库报错 wsarecv: An existing connection was forcibly closed by the remote host.
- Control statement if switch for while while break continue
- P1169 "chessboard making"
- The mobile terminal page uses REM for adaptation
- Opencv oak-d-w wide angle camera test
- Comparison and introduction of OpenCV oak cameras
- 全局池化–Pytorch
- ESP8266_SmartConfig
- Revisiting Self-Training for Few-Shot Learning of Language Model,EMNLP2021
- The difference and relation between machine learning and statistics
猜你喜欢

Bowen dry goods | Apache inlong uses Apache pulsar to create data warehousing
affair

LeetCode刷题 —— 手撕二叉树

Interview questions: REM layout, flex layout, etc

The ins-30131 installer failed to verify the required initial settings

Product list display

Opencv CEO teaches you to use oak (IV): create complex pipelines

ESP8266_ SmartConfig
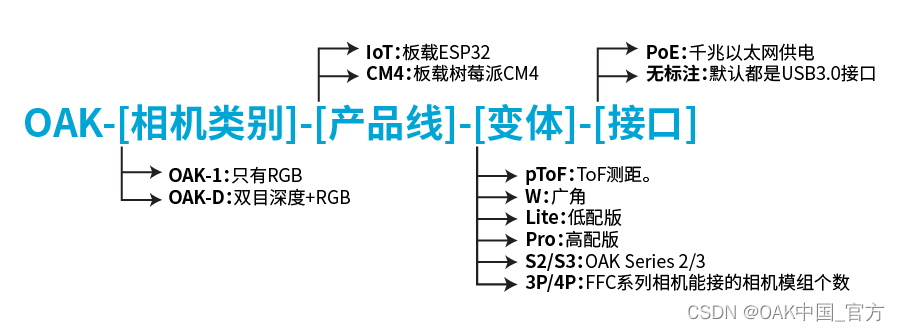
OpenCV OAK相机对比及介绍

Image quality evaluation including Matlab source code
随机推荐
ESP8266_MQTT协议
Where is it safer to open an account for soda ash futures? How much do you need to buy at least?
[scheme development] sphygmomanometer scheme pressure sensor sic160
Esp8266 Smartconfig
Device = depthai Device(““, False) TypeError: _init_(): incompatible constructor arguments.
Interview question 17.10 Main elements
RAC单独修改scanip到不同网段时会报错
Troubleshooting the error ora-12545 reported by scanip in Oracle RAC
ESP8266_ Connect to Alibaba cloud through mqtt protocol
PD chip ga670-10 for OTG while charging
整型提升例题
Redis transaction details
面试常问:rem布局,flex布局等
go连接数据库报错 wsarecv: An existing connection was forcibly closed by the remote host.
MySQL:Got a packet bigger than ‘max_ allowed_ packet‘ bytes
Video review pulsar summit Asia 2021, cases, operation and maintenance, ecological dry goods
Shandong University project training (IV) -- wechat applet scans web QR code to realize web login
How to determine whether two time periods overlap?
ESP8266_SmartConfig
JS foundation - array object

