当前位置:网站首页>Shenji Bailian 3.54-dichotomy of dyeing judgment
Shenji Bailian 3.54-dichotomy of dyeing judgment
2022-07-02 05:59:00 【starnight531】
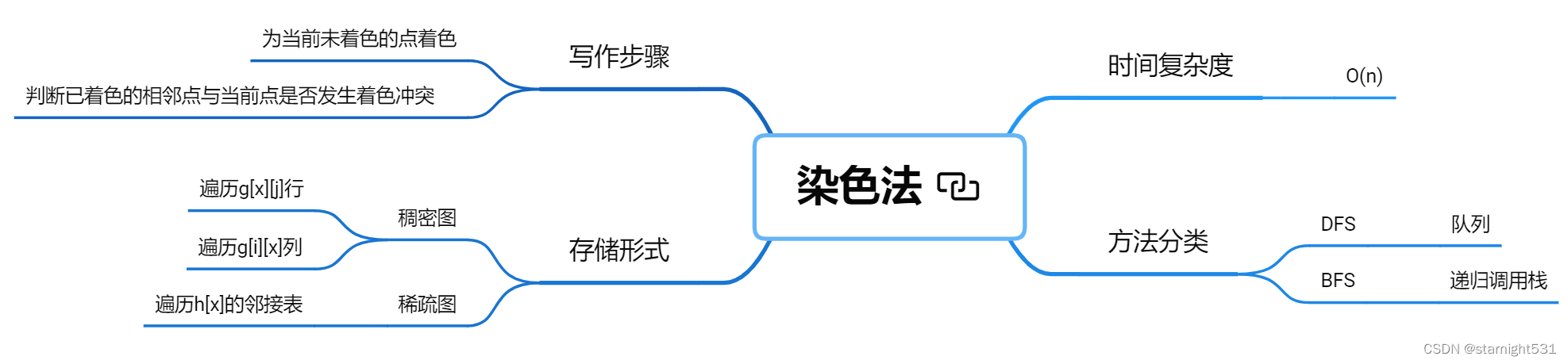
Dyeing method
Food Guide :
Students who are familiar with the algorithm programming and stepping on the pit can directly jump to the code template to view the complete code Only the topic of basic algorithm will have the principle of the algorithm , Implementation steps , Code note , The code template , Explanation of code errors The problem of non basic algorithm focuses on problem analysis , Code implementation , And the necessary code misunderstanding
Title Description :
Given a bipartite graph , The left half contains n1 A little bit ( Number 1∼n1), The right half contains n2 A little bit ( Number 1∼n2), Bipartite graph contains m side .
The data guarantees that neither end point of any edge can be in the same part .
Please find the maximum matching number of bipartite graph .The matching of bipartite graphs : Given a bipartite graph G, stay G A picture of M in ,M Edge set of {E} Any two edges in are not attached to the same vertex , said M It's a match .
The maximum matching of bipartite graphs : The group of matches with the largest number of edges is called the maximum match of bipartite graph , The number of edges is the maximum matching number .Input format
The first line contains three integers n1、 n2 and m.
Next m That's ok , Each line contains two integers u and v, Represents the point in the left half point set u And the point in the right half v There is an edge between .Output format
Output an integer , Represents the maximum number of matches of a bipartite graph .Data range
1≤n1,n2≤500,
1≤u≤n1,
1≤v≤n2,
1≤m≤105
sample input :
2 2 4
1 1
1 2
2 1
2 2
sample output :
2Title source :https://www.acwing.com/problem/content/863/
Topic analysis :
- Classic topic of dyeing : For each point , If it is dyed x color , Then dye its adjacent dots into another color .
Finally, every point in the graph is colored successfully , Then the graph is a bipartite graph .
On the contrary, if there is a dyeing contradiction at some point , It should be dyed x color , It should be dyed in another color , Then the graph is not a bipartite graph . - There are two dyeing methods :dfs Realization & bfs Realization
The following is also O(n) Two coloring methods for determining bipartite graphs
Algorithm principle :
Template algorithm :
- Portal :dfs
- Portal :n queens problem
Dyeing method :
1. Bipartite graph :
- Definition :
For each side , Place its two endpoints in two different sets .
If all points in the final graph are perfectly divided into two different sets , Then the graph is a bipartite graph . - nature :
You can use two colors to color all points in the graph without conflict . - give an example :
Bipartite graph :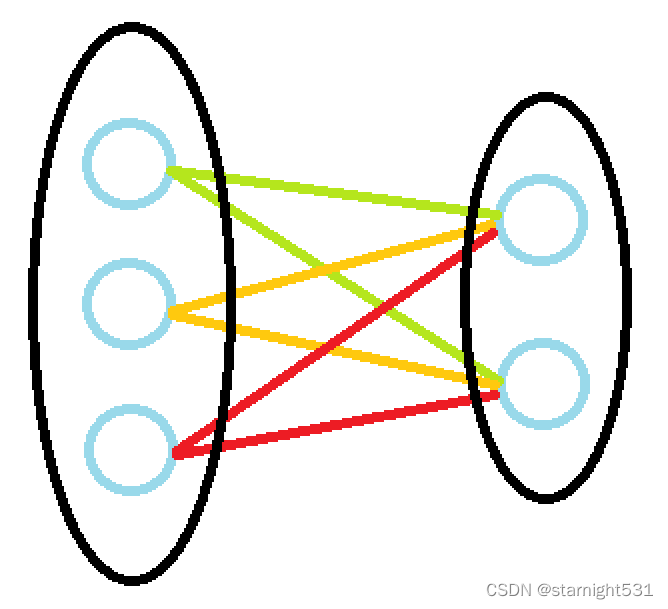
Non bipartite graph :
2. Two big steps :
For each of these points , Regardless of dfs still bfs, There are two tasks :
Shade the current unshaded points & Check whether there is a conflict between the adjacent point and the current point .
Is currently unshaded x Dot dyeing y:
Traverse the current x Adjacency point of point , Judge whether it conflicts with the current point one by one :
If the adjacent contact has been colored , And for y, Then there is coloring conflict , Directly determine non bipartite graph .
If the adjacent contact has been colored , And for y The opposite of , Then continue to color the next adjacent point .
If the adjacent contact is not colored , Then dye it as y The opposite of , Then continue to color the next adjacent point .
Code implementation :
dfs Realize dyeing
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 200020; //m side , be 2m A little bit
int color[N]; // Mark the color of each point , The bipartite graph only needs 1 & 2 Two colors
int h[N], val[N], ne[N];
int idx;
void add(int x, int y){
val[idx] = y;
ne[idx] = h[x];
h[x] = idx++;
}
int n,m;
bool dfs(int x, int y){
color[x] = y;
for(int i = h[x]; i!=-1; i=ne[i]){
if(color[val[i]] == y){
// Check whether shaded points contain shading conflicts
return false;
}else if(!color[val[i]]){
// Shade unshaded points
if(!dfs(val[i],3-y))
return false;
}
}
return true;
}
int main(){
memset(h, -1, sizeof(h));
cin >>n >>m;
int a = 0, b = 0;
while(m--){
cin >>a >>b;
add(a, b);
add(b, a);
}
// It may be a disconnected graph , Every connected component needs coloring
for(int i=1; i<=n; i++){
if(!color[i]){
if (!dfs(i,1)){
cout << "No"<<endl;
return 0;
}
}
}
cout <<"Yes"<<endl;
return 0;
}
bfs Realize dyeing :
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 200020;
int h[N], val[N], ne[N];
int idx;
void add(int x, int y){
val[idx] = y;
ne[idx] = h[x];
h[x] = idx++;
}
int n, m;
int color[N];
int tt = 0, hh = 0;
int que[N];
bool bfs(int x, int y){
que[tt++] = x; // from que[0] Start storage
color[x] = y;
while(hh < tt){
// Start hh==tt==0 when , The queue is empty ; So only hh<tt The queue contains elements
int t = que[hh++];
for(int i=h[t]; i!=-1; i=ne[i]){
if (color[val[i]] == color[t]){
// Check whether there is color conflict between shaded adjacent points
return 0;
}else if (!color[val[i]]){
// Shade unshaded points
color[val[i]] = 3-color[t];
que[tt++] = val[i];
}
}
}
return 1;
}
int main(){
memset(h, -1, sizeof h);
cin >>n >>m;
int a=0, b=0;
while(m--){
cin >>a >>b;
add(a, b);
add(b, a);
}
// Every connected component of a non connected graph needs coloring
for(int i=1; i<=n; i++){
if (!color[i]){
if (!bfs(i, 1)){
cout<< "No";
return 0;
}
}
}
cout<< "Yes";
return 0;
}
Code errors :
1. Conversion skills of two colors :
- Suppose the two colors are x Color and y color , And remember x+y And for s
This stain is x, Then the next stain is s-x
2. Easy leakage point : Unconnected graph
- When a point in the whole graph has been dyed , But there are still some points that are not colored , Explain that the graph is disconnected .
- For each connected component of a non connected graph , Select one of the points for dyeing .
- Each time the staining method is performed , Continue to traverse all points , Check whether there are still undyed connected components .
3. DFS and BFS Similarities :
- When coloring undyed dots , It is found that this point conflicts with the dyed adjacent points .
Thoughts on this article :
The understanding and implementation of dyeing method itself are relatively simple , Just remember two things :
Dye the undyed dots & Check whether the current point conflicts with the dyed adjacent points .
Finish this blog post , Congratulations on having posted 《 Build a foundation - later stage 》

It's not far from entering fairyland , come on. 
边栏推荐
- Go learning notes integration
- keepalived安装使用与快速入门
- 1036 Boys vs Girls
- MySQL transaction and isolation level
- all3dp. All Arduino projects in com website (2022.7.1)
- 1037 Magic Coupon
- How to change the IP address of computer mobile phone simulator
- 1035 Password
- 【論文翻譯】GCNet: Non-local Networks Meet Squeeze-Excitation Networks and Beyond
- Regular expression summary
猜你喜欢
File contains vulnerability (I)

Minimum value ruler method for the length of continuous subsequences whose sum is not less than s
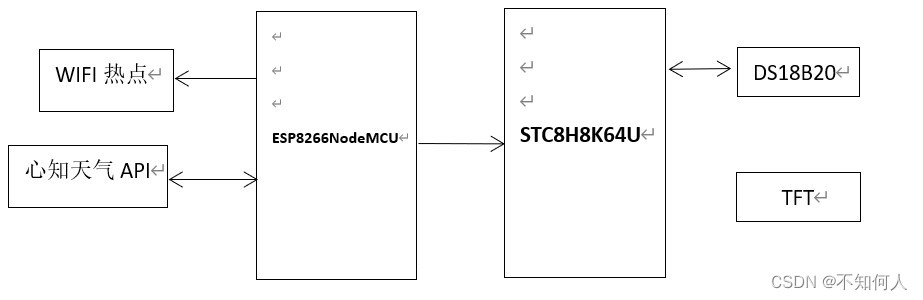
ESP8266与STC8H8K单片机联动——天气时钟

软件测试 - 概念篇

ES6的详细注解

Zabbix Server trapper 命令注入漏洞 (CVE-2017-2824)

How to write good code - Defensive Programming Guide

Regular expression summary

3D printer G code command: complete list and tutorial
深度学习分类网络 -- AlexNet
随机推荐
keepalived安装使用与快速入门
页面打印插件print.js
在uni-app中引入uView
RGB infinite cube (advanced version)
1037 Magic Coupon
STC8H8K系列汇编和C51实战——数码管显示ADC、按键串口回复按键号与ADC数值
mysql的约束总结
token过期自动续费方案和实现
Page printing plug-in print js
神机百炼3.53-Kruskal
495.提莫攻击
Eco express micro engine system has supported one click deployment to cloud hosting
Brain and cognitive neuroscience matlab psychoolbox cognitive science experimental design - experimental design 4
Ti millimeter wave radar learning (I)
软件测试基础篇
Stick to the big screen UI, finereport development diary
[leetcode] day92 container with the most water
数理统计与机器学习
文件包含漏洞(二)
Go learning notes integration