当前位置:网站首页>高数中值定理总结
高数中值定理总结
2022-07-06 22:42:00 【全栈O-Jay】
中值定理
一般用于证明题,分析步骤:确定区间、确定辅助函数、确定使用的定理、关键点分析。
f(x)在[a,b]上连续,
- 有界与最值定理: m ≤ f ( x ) ≤ M m \leq f(x)\leq M m≤f(x)≤M
- 介值定理: m ≤ μ ≤ M , ∃ ϵ ∈ [ a , b ] , f ( ϵ ) = μ m\leq \mu \leq M, \exists \epsilon \in[a,b], f(\epsilon) = \mu m≤μ≤M,∃ϵ∈[a,b],f(ϵ)=μ
- 平均值定理: a < x 1 < x 2 < ⋯ < x n < b , ∃ ϵ ∈ [ x 1 , x n ] , f ( ϵ ) = f ( x 1 ) + f ( x 2 ) + ⋯ + f ( x n ) n a<x_1<x_2<\cdots<x_n<b, \exists \epsilon \in[x_1,x_n], f(\epsilon) = \frac{f(x_1)+f(x_2)+\cdots+f(x_n)}{n} a<x1<x2<⋯<xn<b,∃ϵ∈[x1,xn],f(ϵ)=nf(x1)+f(x2)+⋯+f(xn)
- 零点定理: f ( a ) ⋅ f ( b ) < 0 , ∃ ϵ ∈ [ a , b ] , f ( ϵ ) = 0 f(a)\cdot f(b)<0, \exists \epsilon \in[a,b], f(\epsilon) = 0 f(a)⋅f(b)<0,∃ϵ∈[a,b],f(ϵ)=0
- 费马定理: x 0 处 可 导 且 为 极 值 , f ′ ( x 0 ) = 0 x_0处可导且为极值, f'(x_0) = 0 x0处可导且为极值,f′(x0)=0
- 罗尔定理: [ a , b ) 可 导 , f ( a ) = f ( b ) , ∃ ϵ ∈ [ a , b ] , f ′ ( ϵ ) = 0 [a,b)可导, f(a) = f(b), \exists \epsilon \in[a,b], f'(\epsilon) = 0 [a,b)可导,f(a)=f(b),∃ϵ∈[a,b],f′(ϵ)=0
- 拉格朗日中值定理: ( a , b ) 可 导 , ∃ ϵ ∈ [ a , b ] , f ( b ) − f ( a ) = f ′ ( ϵ ) ( b − a ) (a,b)可导, \exists \epsilon \in[a,b], f(b) - f(a) = f'(\epsilon)(b-a) (a,b)可导,∃ϵ∈[a,b],f(b)−f(a)=f′(ϵ)(b−a)
- 柯西中值定理: ( a , b ) 可 导 , g ′ ( x ) ≠ 0 , ∃ ϵ ∈ [ a , b ] , f ( b ) − f ( a ) g ( b ) − g ( a ) = f ′ ( ϵ ) g ′ ( ϵ ) (a,b)可导, g'(x)\neq 0, \exists \epsilon \in[a,b], \frac{f(b) - f(a)}{g(b) - g(a)} = \frac{f'(\epsilon)}{g'(\epsilon)} (a,b)可导,g′(x)=0,∃ϵ∈[a,b],g(b)−g(a)f(b)−f(a)=g′(ϵ)f′(ϵ)
- 泰勒公式(拉格朗日余项): f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + ⋯ + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + f ( n + 1 ) ( ϵ ) ( n + 1 ) ! ( x − x 0 ) n + 1 f(x) = f(x_0) + f'(x_0)(x-x_0)+\cdots+ \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n +\frac{f^{(n+1)}(\epsilon)}{(n+1)!}(x-x_0)^{n+1} f(x)=f(x0)+f′(x0)(x−x0)+⋯+n!f(n)(x0)(x−x0)n+(n+1)!f(n+1)(ϵ)(x−x0)n+1
- 泰勒公式(佩亚诺余项): f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + ⋯ + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + O ( ( x − x 0 ) n ) f(x) = f(x_0) + f'(x_0)(x-x_0)+\cdots+ \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n +O((x-x_0)^n) f(x)=f(x0)+f′(x0)(x−x0)+⋯+n!f(n)(x0)(x−x0)n+O((x−x0)n)
- 积分中值定理: ∃ ϵ ∈ [ a , b ] , ∫ a b f ( x ) d x b − a = f ( ϵ ) \exists \epsilon \in[a,b], \frac{\int_a^bf(x)dx}{b-a} = f(\epsilon) ∃ϵ∈[a,b],b−a∫abf(x)dx=f(ϵ)
有个记忆技巧,最常用的就七个,“零介费罗拉泰西”,看到证明题没思路可以一一试试,
边栏推荐
- 【736. Lisp 语法解析】
- You can't sell the used lithography machine to China! The United States unreasonably pressured the Dutch ASML, and domestic chips were suppressed again
- 关于01背包个人的一些理解
- 九章云极DataCanvas公司蝉联中国机器学习平台市场TOP 3
- U++ 元数据说明符 学习笔记
- R descriptive statistics and hypothesis testing
- 使用Thread类和Runnable接口实现多线程的区别
- 动态生成表格
- Section 1: (3) logic chip process substrate selection
- STM32F103 realize IAP online upgrade application
猜你喜欢
Ansible overview and module explanation (you just passed today, but yesterday came to your face)

【愚公系列】2022年7月 Go教学课程 005-变量
How to package the parsed Excel data into objects and write this object set into the database?
九章云极DataCanvas公司蝉联中国机器学习平台市场TOP 3
Oracle -- 视图与序列

Liste des hôtes d'inventaire dans ansible (je vous souhaite des fleurs et de la romance sans fin)
指针与数组在函数中输入实现逆序输出
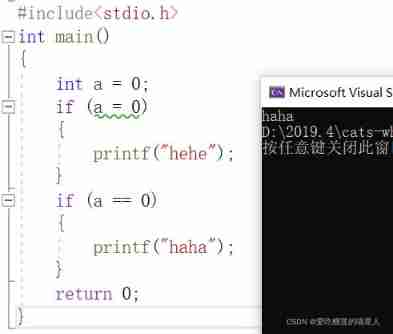
Meow, come, come: do you really know if, if else
Operand of null-aware operation ‘!‘ has type ‘SchedulerBinding‘ which excludes null.
namespace基础介绍
随机推荐
Two methods of chromosome coordinate sequencing
[Yugong series] go teaching course 005 variables in July 2022
当 Knative 遇见 WebAssembly
【Android Kotlin协程】利用CoroutineContext实现网络请求失败后重试逻辑
Oracle -- 视图与序列
Ansible reports an error: "MSG": "invalid/incorrect password: permission denied, please try again“
Jetson nano configures pytorch deep learning environment / / to be improved
Analysis -- MySQL statement execution process & MySQL architecture
JS variable case
5G VoNR+之IMS Data Channel概念
Section 1: (3) logic chip process substrate selection
mpf2_ Linear programming_ CAPM_ sharpe_ Arbitrage Pricin_ Inversion Gauss Jordan_ Statsmodel_ Pulp_ pLU_ Cholesky_ QR_ Jacobi
leetcode 53. Maximum subarray maximum subarray sum (medium)
3GPP信道模型路损基础知识
Gavin teacher's perception of transformer live class - rasa project actual combat e-commerce retail customer service intelligent business dialogue robot microservice code analysis and dialogue experim
Local tool [Navicat] connects to remote [MySQL] operation
Common Oracle SQL statements
What work items do programmers hate most in their daily work?
You can't sell the used lithography machine to China! The United States unreasonably pressured the Dutch ASML, and domestic chips were suppressed again
Meow, come, come: do you really know if, if else