Combinatorics Notes (6) Associative Algebra of Locally Finite Partially Ordered Sets, Möbius Inversion Formula

---

tags: Combinatorics

写在前面

There are a lot of partially ordered sets and lattices in the front,Basic knowledge of distributive lattice, etc, Let's start with these algebraic structures as research objects, Explore some of its properties and relationships, Let's start with the definition of associative algebra.

Introduction to associative algebra

定义

• 令$\mathrm{Int}(P)$表示$P$The set of all the intervals above, (The empty set is not an interval)
• 令$K$为一个域, 定义$f:\mathrm{Int}(P)\to K$, 用$f(x,y)$表示$f([x,y])$.

$P$在$K$上的Associative Algebra$I(P,K)$定义为: by all functions$f:\mathrm{Int}(P)\to K$构成的$K$-代数, 其中乘法(卷积)定义为:

$$(fg)(x,y)=\sum _{x\le {}_{\stackrel{{}_z}{{}^{\cdot }}}\le y}f(x,z)g(z,y).$$

and associative algebra$I(P,K)$There is a combination of bilateral unit cells$K$-代数, 单位元记为$\delta$或者$1$,定义为

KaTeX parse error: Undefined control sequence: \mbox at position 34: …in{cases} 1, & \̲m̲b̲o̲x̲{if}\ x=y,\\ 0…

number field$K=\mathbb{C}$即可, 可将$I(P,\mathbb{C})$简记为$I(P)$.

---

另一种表达:

将$I(P,K)$Treated by all formal expressions:

$$f=\sum _{[x,y]\in \mathrm{Int}(P)}f(x,y)[x,y]$$

组成的, where convolution is defined as follows:

KaTeX parse error: Undefined control sequence: \mbox at position 39: …{cases} [x,w],&\̲m̲b̲o̲x̲{if }y=z,\\[5pt…

and by bilinear(允许$[x,y]$infinite linear combination of )extended to all$I(P,K)$.

Examples of limited cases

如果$P$有限, The elements are denoted as $x_1,\cdots ,x_n$, 其中$x_i<x_j\Rightarrow i<j$, 于是$I(P)$同构于$\mathbb{C}$上满足: 若$x_i\nleqq x_j$则$m_{ij}=0$的上三角矩阵$M=(m_{ij}),1\le i,j\le n$constituted algebra. (可以从$m_{ij}$到$f(x_i,x_j)$建立映射关系)

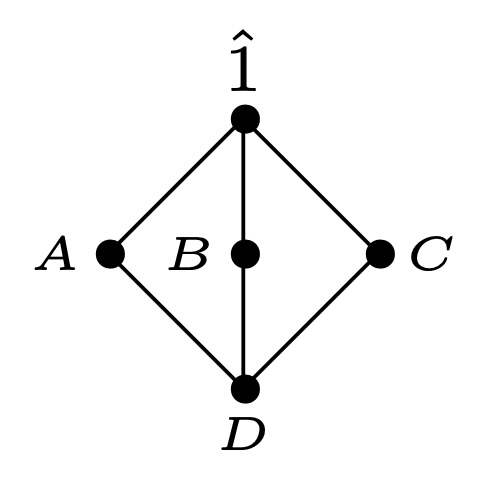
如果$P$由下图给出, 则$I(P)$Isomorphic to form

$$ \begin{bmatrix} ∗ & 0 & ∗ & 0 & ∗\\ 0 & ∗ & ∗ & ∗ & ∗\\ 0 & 0 & ∗ & 0 & ∗\\ 0 & 0 & 0 & ∗ & ∗\\ 0 & 0 & 0 & 0 & ∗\\ \end{bmatrix} $$ The algebra of matrix formation.

性质

设$f\in I(P)$, Then the following conditions are equivalent:

• $f$has a left inverse;
• $f$has a right inverse;
• $f$There is a two-sided inverse(Must be the only left and right inverse);
• $f(x,x)\ne 0,\forall x\in P$成立.

进一步, 如果$f^{-1}$存在, 则$f^{-1}(x,y)$Depends only on partially ordered sets$[x,y]$.

证明:

设$fg=\delta$, 等价于$\forall x\in P$, 有$f(x,x)g(x,x)=1$, $\forall x,y\in P$, 且满足$x<y$, 有

KaTeX parse error: Limit controls must follow a math operator at position 35: …-1}{\large\sum}\̲l̲i̲m̲i̲t̲s̲_{x<z\le y}f(x,…

于是$f$has a right inverse$g*\forall x\in P,f(x,x)\ne 0$, 并且此时$f^{-1}(x,y)$仅取决于$[x,y]$.

同理, 设$hf=\delta$, 即得到$f$has a right inverse$*\forall x\in P,f(x,x)\ne 0*f$has a right inverse.

另外, 由$fg=\delta ,hf=\delta$, 得到$g=h$.

Useful functions in associative algebra

zeta函数

$\zeta (x,y)=1,\forall x,y\in P,x\le y$. 所以有

KaTeX parse error: Undefined control sequence: \mbox at position 52: …{x\le z\le y}1=\̲m̲b̲o̲x̲{card}[x,y],\\[…

即从$x$到$y$的长度为$k$the number of heavy chains. 类似有

$$(\zeta -1)(x,y)=\{\begin{array}{ll}1,& x<y,\\ 0,& x=y.\end{array}$$

于是$(\zeta -1{)}^k(x,y)$是从$x$到$y$的长度为$k$的链$x=x_0<x_1<\cdots <x_k=y$的条数.

下面是$(2-\zeta )(x,y)\in I(P)$,

$$(2-\zeta )(x,y)=\{\begin{array}{ll}1,& x=y,\\ -1,& x<y.\end{array}$$

Möbius反演

discussed above, 局部有限偏序集$P$的zeta函数$\zeta$可逆, Its inverse is called$P$的Möbius函数, 记为$\mu$(或者${\mu }_P$). Definition by induction, 可得到:

KaTeX parse error: Expected group after '_' at position 111: … \mu(x,y)=-\sum_̲\limits{x\le z<…

The second formula can be passed directly$(1)$After substituting in the formula, it is expanded.

Möbius反演公式

设$P$is a partially ordered set that is ideally finite for all main orders, 令$f,g:P\to \mathbb{C}$, 有

$$g(x)=\sum _{y\le x}f(y),\forall x\in P,\text{\hspace{1em}(2)}$$

当且仅当

$$f(x)=\sum _{y\le x}g(y)\mu (y,x),\forall x\in P.$$

See the original English book for this proof. There is a way to prove it by trivial computation, I feel a little better to understand.(The role of subspaces is a bit abstract) 假定$(2)$成立, 则有

$$\begin{array}{rl}\sum _{y\le x}g(y)\mu (y,x)& =\sum _{y\le x}\mu (y,x)\sum _{z\le y}f(z)\\ & =\sum _{z\le x}f(z)\sum _{z\le y\le x}\mu (y,x)\\ & =\sum _{z\le x}f(z)\delta (z,x)=f(x)\end{array}$$

where the penultimate equal sign holds because :

$$\delta (z,x)=(\zeta \mu )(z,x)=\sum _{z\le y\le x}\zeta (z,y)\mu (y,x)=\sum _{z\le y\le x}\mu (y,x)$$

对偶形式

设$P$is an all-primary-dual order ideal$V_x$are finite partially ordered sets, 令$f,g\in {\mathbb{C}}^P$, 则有

$$g(x)=\sum _{y\ge x}f(y),\forall x\in P,$$

当且仅当

$$f(x)=\sum _{y\ge x}\mu (x,y)g(y),\forall x\in P.$$

一个例子: MöbiusThe meaning of the inversion formula

Recall an example from the beginning of this chapter: 有限集合$A,B,C,D$, 满足:

$$D=A\cap B=A\cap C=B\cap C=A\cap B\cap C,$$

通过容斥原理得到:

$$\begin{array}{rl}|A\cup B\cup C|& =|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|\\ & =|A|+|B|+|C|-2|D|\end{array}$$

下面通过MöbiusInversion explains the above equation:

给定$n$a limited set$S_1,...,S_n$, 令$P$for them allThe intersection is under the containment relationPartially ordered set, This includes air delivery$S_1\cup \cdots \cup S_n=\hat{1}$, 若$T\in P$, 令$f(T)$表示$P$中属于$T$但不属于任何$T^{\prime }<T$的元素的个数, 令$g(T)=|T|$.

The following is found by the above inversion formula

$$|S_1\cup \cdots \cup S_n|=\sum _{T\le \hat{1}}f(T)=g(\hat{1}),$$

的表达式, 已知:

$$g(T)=\sum _{T^{\prime }\le T}f(T^{\prime }),$$

由$P$上的Möbius反演得到

$$\begin{array}{rl}0=f(\hat{1})& =\sum _{T\in P}g(T)\mu (T,\hat{1})\\ & =\sum _{T\le \hat{1}}g(T)\mu (T,\hat{1})\\ & =g(\hat{1})\mu (\hat{1},\hat{1})+\sum _{T<\hat{1}}|T|\mu (T,\hat{1})\\ \Rightarrow g(\hat{1})& =-\sum _{T<\hat{1}}|T|\mu (T,\hat{1}).\end{array}$$

于是, The above example can be directly given by the inversion formula(Hasse图如下), 其中

$$\begin{array}{rl}0& =\delta (A,\hat{1})=(\mu \zeta )(A,\hat{1})\\ & =\sum _{A\le z\le \hat{1}}\mu (A,z)\zeta (z,\hat{1})\\ & =\mu (A,A)\zeta (A,\hat{1})+\mu (A,\hat{1})\zeta (\hat{1},\hat{1})=1+\mu (A,\hat{1})\\ \Rightarrow & \mu (A,\hat{1})=\mu (B,\hat{1})=\mu (C,\hat{1})=-1\end{array}$$

$$\begin{array}{rl}0& =\delta (D,\hat{1})=(\mu \zeta )(D,\hat{1})\\ & =\sum _{D\le z\le \hat{1}}\mu (D,z)\zeta (z,\hat{1})\\ & =\mu (D,D)\zeta (D,\hat{1})+\mu (D,A)\zeta (A,\hat{1})+\mu (D,B)\zeta (B,\hat{1})\\ & +\mu (D,C)\zeta (C,\hat{1})+\mu (D,\hat{1})\zeta (\hat{1},\hat{1})\\ & =1+(-3)+\mu (D,\hat{1})\\ \Rightarrow & \mu (D,\hat{1})=2\end{array}$$