李航《统计学习方法》笔记之朴素贝叶斯法

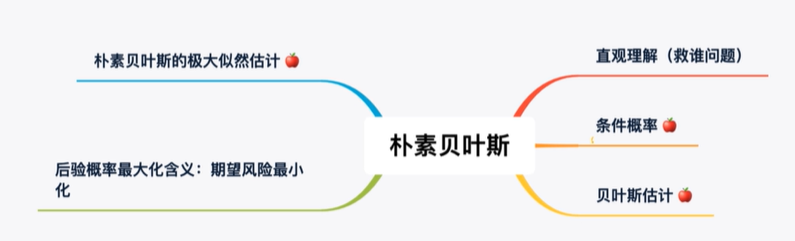
第4章朴素贝叶斯法

朴素是整个算法的强假设，即变量之间是强相互独立的。

例子

路人拿出来3颗豆，两颗红豆1颗绿豆，我和路人各自抽了一颗,路人发现自己抽中的是绿豆，他想用剩下的那颗和我换，我换不换?换不换豆，抽中红豆概率一样吗?

$P(A\mid B)$ 表示在B发生的条件下发生A的概率。

$P(A\mid B)=\frac{P(AB)}{P(B)}=\frac{P(B\mid A)P(A)}{P(B)}$

设A表示我抽中的是红豆，B表示路人抽中的是绿豆

$P(A\mid B)=\frac{P(B\mid A)P(A)}{P(B)}=\frac{1\cdot \frac{1}{3}}{1}=\frac{1}{3}$

注意这里的一个误区，由于是在已知B抽中的是绿豆的前提下，因此，这里$P(B)=1$而不是$\frac{2}{3}$。

结论:如果要红豆，最好和路人交换一下。如果要绿豆，最好不要换。

假设有一个手写数据集,里面有100条记录,其中第0-9条记录是10个人分别写的0。10-19条是10个人分别写的1。……。第90-99条是10个人分别写的10，写了一个数字X，怎么判断是数字几呢?
朴素贝叶斯工作原理:

$P(Y=0\mid X)=?,P(Y=1\mid X)=?,\cdots \cdots ,P(Y=10\mid X)=?$

找到概率值最高的，就是对应的数字。

数学表达就是：

对于刚刚的手写数据集, 我们设数字的类别为 $C_{k}, C_{0} $表示数字 $0, \cdots \cdots $。刚才数字判别公式可以修改为 $P{\left(Y=C_{\mathbf{k}}\mid X=x\right)}_{\text{。 }}$

$\begin{array}{rl}P\left(Y=C_{\mathrm{k}}\mid X=x\right)=& \frac{P\left(X=x\mid Y=C_k\right)P\left(Y=C_k\right)}{P(X=x)}\\ =& \frac{P\left(X=x\mid Y=C_k\right)P\left(Y=C_k\right)}{{\sum }_{k}P\left(X=x,Y=C_k\right)}\\ =& \frac{P\left(X=x\mid Y=C_k\right)P\left(Y=C_k\right)}{{\sum }_{k}P\left(X=x\mid Y=C_k\right)P\left(Y=C_k\right)}\end{array}$

并且由于每一张图片是8x8的像素点组成，可以看作一个一维64数组，这里是把样本X拆开

$\begin{array}{rl}\mathrm{P}\left(X=x\mid Y=C_k\right)& =P\left(X^{(1)}=x^{(1)}\mid Y=C_k\right)P\left(X^{(2)}=x^{(2)}\mid Y=C_k\right)\cdots P\left(X^{(j)}=x^{(j)}\mid Y=C_k\right)\\ & =\prod _{j}P\left(X^{(j)}=x^{(j)}\mid Y=C_k\right)\end{array}$

因此上式可以化简为：

KaTeX parse error: Expected 'EOF', got '&' at position 45: …d X = x\right) &̲ = \frac{P\left…

$\begin{array}{rl}f(x)=\underset{C_k}{\mathrm{argmax}}P\left(Y=C_k\mid X=x\right)& =\frac{P\left(Y=C_k\right){\prod }_{j}P\left(X^{(j)}=x^{(j)}\mid Y=C_k\right)}{{\sum }_{k}P\left(Y=C_k\right){\prod }_{j}P\left(X^{(j)}=x^{(j)}\mid Y=C_k\right)}\\ & =P\left(Y=C_k\right)\prod _{j}P\left(X^{(j)}=x^{(j)}\mid Y=C_k\right)\end{array}$

其中$\underset{C_k}{\mathrm{argmax}}$意味找到让后面这个概率最大的$C_k$，其中：

$\begin{array}{l}{\sum }_k{\prod }_{j}p(X^{(j)}=x^{(j)}\mid Y=C_k)p(Y=C_k)\\ ={\sum }_k{\sum }_{j}p\left(X^{(j)}=x^{(j)},Y=C_k\right)={\sum }_{j}P\left(X^{(j)}=x^{(j)}\right)\\ =P(X=x)\end{array}$

朴素贝叶斯法的参数估计

极大似然估计

在朴素贝叶斯法中, 学习意味着估计 $P\left(Y=c_k\right)$ 和 $P\left(X^{(j)}=x^{(j)}\mid Y=c_k\right)$ 。可以 应用极大似然估计法估计相应的概率。先验概率 $P\left(Y=c_k\right)$ 的极大似然估计是

$P\left(Y=c_k\right)=\frac{{\sum }_{i=1}^{N}I\left(y_i=c_k\right)}{N},k=1,2,\cdots ,K$

设第 j 个特征 $x^{(j)} $ 可能取值的集合为 $\left\{a_{j1},a_{j2},\cdots ,a_{j{S}_j}\right\}$, 条件概率 $P(X^{(j)}=a_{jl}\mid Y=c_k)$ 的极大似然估计是

$\begin{array}{l}P\left(X^{(j)}=a_{jl}\mid Y=c_k\right)=\frac{{\sum }_{i=1}^{N}I\left(x_i^{(j)}=a_{jl},y_i=c_k\right)}{{\sum }_{i=1}^{N}I\left(y_i=c_k\right)}\\ j=1,2,\cdots ,n;l=1,2,\cdots ,S_j;k=1,2,\cdots ,K\end{array}$

式中, $x_i^{(j)}$ 是第 i 个样本的第 j 个特征; $a_{jl}$ 是第 j 个特征可能取的第 l 个值; $I$ 为指 示函数。