当前位置:网站首页>浮点数的运算方法
浮点数的运算方法
2022-08-02 14:03:00 【君知燕云归】
一、浮点数的表示
1.浮点数的表示
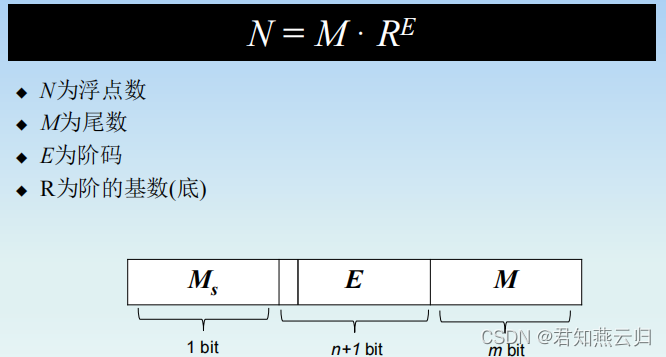
Ms表示尾数的符号位,E中1bit保存阶码的符号位其余空间存放阶码值,M中存放规格化后的尾数。
因为尾数规格化后其绝对值应大于或等于0.5D,故小数点后第一位都是1,故从小数点后第二位开始保存即可,节省空间并提高精度。
机器零的表示:
2.IEEE 754标准
预备知识:
◆ 单精度浮点数(32位),阶码8位,尾数为24位(内含1位符号位)
◆ 双精度浮点数(64位),阶码为11位,尾数为53位(内含1位符号位)
◆ 基数为2
◆ 阶码采用增码(即移码),尾数采用原码
◆ 规格化原码尾数最高位 1 不在尾数中表示出来
* 恒为1,计算时在尾数的前面自动添加1.
* 隐含的1是一位整数(即位权为20)
为什么阶码采用移码:便于比较浮点数的大小
移码(增码)的特点
◆ 最高位为符号位,1表示正数,0表示负数(不同于原码,补码,反码的符号位规定,更符合人们对数值大小的认知。)
◆ 移码只执行加减法运算—专为阶码而生
◆ 需要对运算结果修正,修正量为2n
◆ 数据零有唯一的编码
IEEE 754标准:
单精度浮点数(32位),阶码8位,尾数为24位(内含1位符号位) ,偏置值127(二进制:1111111)
◆ 基数为2
◆ 阶码采用增码(即移码),尾数采用原码
◆ 规格化原码尾数最高位 1 不在尾数中表示出来
* 恒为1,计算时在尾数的前面自动添加1.
* 隐含的1是一位整数(即位权为 2 0 2^{0} 20)
标准化过程: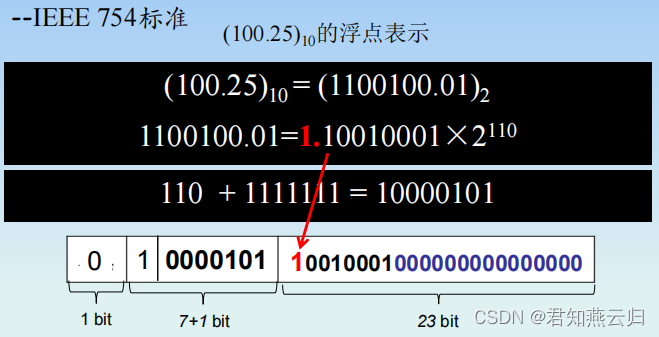
3.浮点数类型
C语言中的浮点数类型
◆ float (十进制有效数字位数为7位)
◆ double(十进制有效数字位数为17位)
◆ 扩展双精度 long double
* 长度和格式由编译器和处理器类型决定
◆ 强制类型转换
* int->float, 不会发生溢出,有效数字可能被舍去
* int/float->double, 没有问题
* double->float, 可能发生溢出,数据可能被舍入
* float/double->int, 可能发生溢出
◆ 将大的浮点数转换为整数可能会导致程序错误
二、浮点数的加减法
1.定义
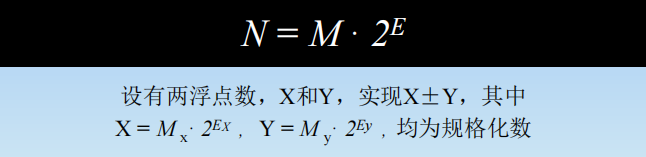
2.运算步骤
- “对阶”操作---- Ex=Ey
求 △E=E-min(Ex, Ey); E=max(Ex, Ey),△E≠0
将阶码小的数的尾数右移△E位
原码:符号位不参加移位,尾数数值部分高位补0
补码:符号位参加移位,并保持原符号位不变
- 尾数的加减运算
执行对阶后,两尾数进行加/减运算,得到两数之和/差。
- 规格化操作
双符号位的原码规格化尾数,其数值的最高位为1
双符号位的补码规格化尾数,应是00.1xx…x或11.0xx…x
规格化规则:
如果结果的两个符号位的值不同,表示加减法运算尾数结果溢出。此时将尾数结果右移1位,阶码E+1,称为向右规格化,简称“右规”。
如果结果的两个符号位的值相同,表示加减法运算尾数结果不溢出。**若最高数值位与符号位相同,此时尾数连续左移,直到最高数值位与符号位的值不同为止。**同时 E-m(移位的位数) ,称为向左规格化,简称“左规”。
- 舍入
执行右规或对阶时,尾数低位上的数值会移掉,使数值的精度受到影响。常用0舍1入法。
当末尾移掉的最高位为1时,在尾数的末位加1.如果加1后又使尾数溢出,则要再进行一次右规。
- 检查阶码是否溢出
若阶码下溢,运算结果为机器零(通常将阶码和尾数全部置“0”);若上溢,则置溢出标志。

二进制移位:左移一位相当于乘2,右移一位相当于除2。
例题演示: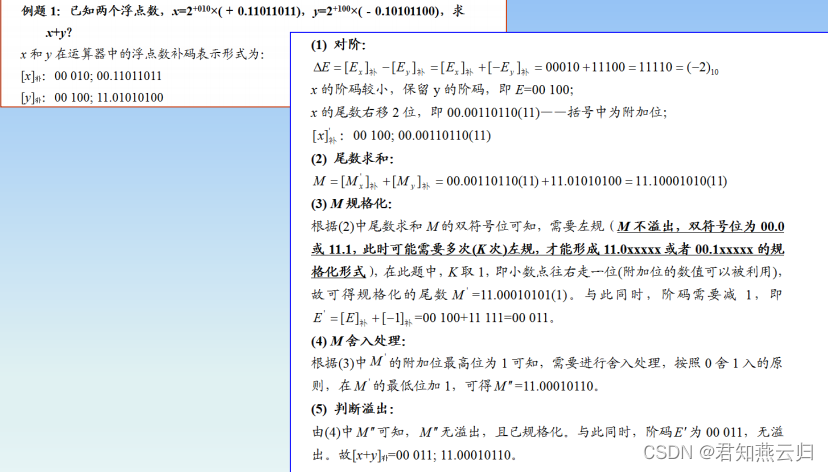
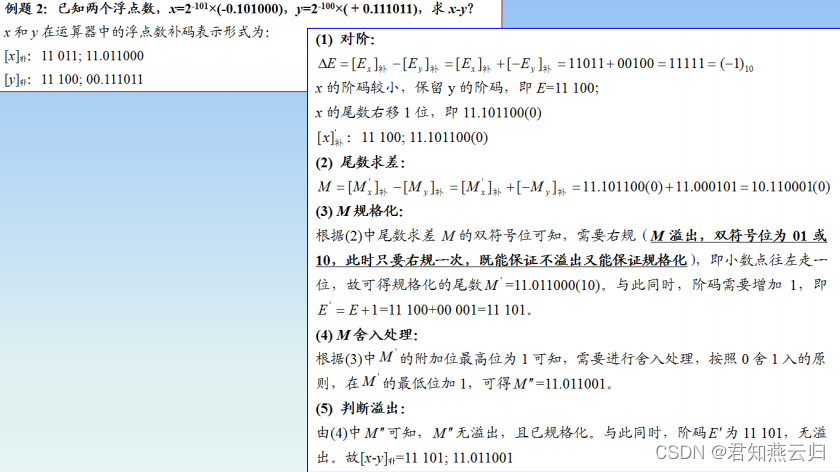
三、运算部件
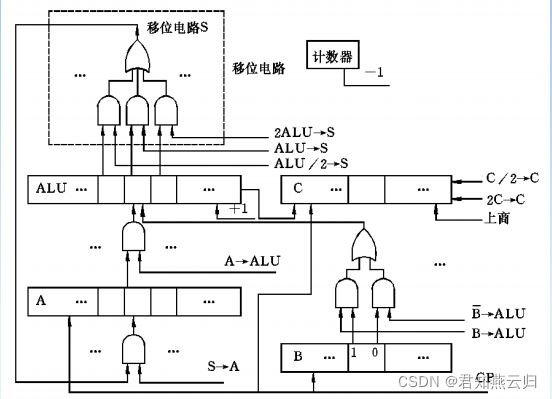
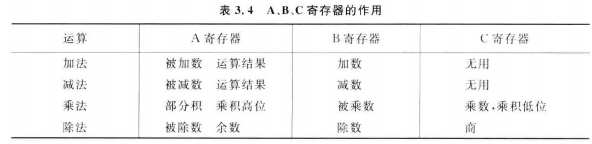



四、强化练习

解析:

解析:本题的关注点是精确二字。A的二进制是无限不循环小数;B的二进制是1.01;C的二进制是10.0;D的二进制是10.1;故不能精确表示的是A。
解析:
边栏推荐
- Unit 11 Serializers
- jwt (json web token)
- 8576 Basic operations of sequential linear tables
- C语言初级—从键盘接收一个整形并逆序输出
- Network pruning (1)
- Steps to connect the virtual machine with xshell_establish a network connection between the host and the vm virtual machine
- 【VCU】详解S19文件(S-record)
- C语言日记 5 运算符和表达式
- 跑yolov5又出啥问题了(1)p,r,map全部为0
- Unit 3 view layer
猜你喜欢
随机推荐
redis delay queue
[ROS](01)创建ROS工作空间
Network pruning (1)
Flask framework in-depth
Flask contexts, blueprints and Flask-RESTful
【ROS】编译软件包packages遇到进度缓慢或卡死,使用swap
Hands-on OCR (1)
第十二单元 关联序列化处理
drf view component
Chapter6 visualization (don't want to see the version)
The language of initial
[ROS] (06) ROS Communication - Topic Communication
[ROS] (02) Create & compile ROS package Package
verilog学习|《Verilog数字系统设计教程》夏宇闻 第三版思考题答案(第七章)
猜数字游戏,猜错10次关机(srand、rand、time)随机数生成三板斧(详细讲解!不懂问我!)
verilog学习|《Verilog数字系统设计教程》夏宇闻 第三版思考题答案(第十章)
Briefly write about the use and experience of PPOCRLabel
verilog学习|《Verilog数字系统设计教程》夏宇闻 第三版思考题答案(第十四章)
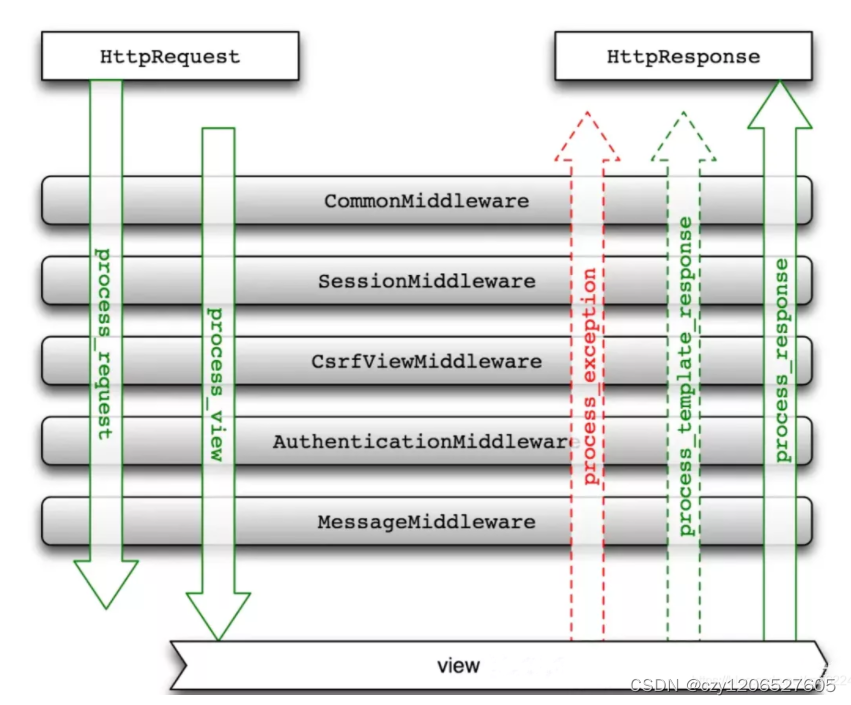
Unit 8 Middleware
8580 Merge linked list
![[ROS] (05) ROS Communication - Node, Nodes & Master](/img/f5/c541259b69a0db3dc15a61e87f0415.png)